Лабораторная работа № 1 циклы и ветвления
Цель работы – приобрести навыки составления программ с использованием условного оператора и операторов цикла.
Условный оператор. Предназначен для записи условного (разветвляющегося) алгоритма.
См стр. 80 Подбельский В.В.
Условное выражение.
См стр. 61 Подбельский В.В.
Переключатель. Предоставляет возможность многовариантного выбора действий в зависимости от значения некоторого выражения. Общий вид оператора см на странице 126 учебника Подбельского В.В.:
Следующие операторы предназначены для записи циклических алгоритмов. Теорию смотрите на стр. 90-92 учебника Подбельского.
Оператор цикла WHILE.
Оператор цикла DO … WHILE.
Оператор цикла с параметром FOR.
Варианты заданий к лабораторной работе
1. Даны натуральное число п, целые числа а 1 ,..., ап. Найти количество и сумму тех членов данной последовательности, которые делятся на 5 и не делятся на 7.
2. Ввести действительные числа x, y (x ≠ y). Меньшее заменить их полусуммой, а большее – их удвоенным произведением. Вывести новые значения x и y на экран.
Решение задачи повторить для нескольких вариантов x, y, для этого после каждого прогона задачи, спросить пользователя, следует ли повторить решение задачи.
3. Дано натуральное число п. Найти наибольшее среди чисел
ke sin / k + 1 (k = l,...,п), а также сумму всех этих чисел.
Решение задачи повторить для нескольких вариантов x, y, для этого после каждого прогона задачи, спросить пользователя, следует ли повторить решение задачи.
4. Если сумма трех различных действительных чисел x, y, z меньше единицы, то наименьшее из этих чисел заменить полусуммой двух других. В противном случае заменить меньшее из чисел x и у полусуммой двух оставшихся значений.
Решение задачи повторить для нескольких вариантов x, y, z для этого после каждого прогона задачи, спросит пользователя, повторить ли решение задачи.
5. Дано натуральное число п. Выбросить из записи числа n цифры 0
и 5, оставив прежним порядок остальных цифр. Например, из числа 59015509 должно получиться 919.
6. Даны натуральное число n, целые числа а1,…,а n (последовательности идущих подряд членов), состоящие из степеней пятерки. Определить для каждого числа степень пятерки.
Программу оформить в виде диалога. Выход из программы – по клавише Esc.
7. Ввести действительные числа а, b, с (а ≠0). Выяснить, имеет ли уравнение ах 2 + b х+с= 0 действительные корни. Если действительные корни имеются, то найти их и вывести на экран. В противном случае ответом должно служить сообщение, что действительных корней нет.
8. Ввести действительное число h. Определить, имеет ли уравнение ах2+ b х+с= 0 действительные корни, если
 ,
,  ,
,  .
.
Если действительные корни существуют, то найти их и вывести на экран. В противном случае, ответом должно служить сообщение, что действительных корней нет.
9. Вычислять сумму чисел натурального ряда, делящихся на 3, до тех пор, пока сумма не превысит 500. Определить число членов суммы.
Числа, делящиеся на 3, и их количестов, значение суммы вывести на экран с соответствующими комментариями.
10. Ввести действительные числа а, b, с (а ≠0). Полностью исследовать биквадратное уравнение ах2+ b х+с= 0. Если действительных корней нет, то должно быть выдано сообщение об этом. Иначе должны быть выведены два или четыре корня.
11. Даны натуральное число п, действительные числа a l ,..., ап. В последовательности a 1,..., ап определить число соседств:
а) двух положительных чисел;
б) двух чисел разного знака;
в) двух чисел одного знака, причем модуль первого числа должен быть больше модуля второго числа.
12. Дано натуральное число n. Получить все его натуральные делители.
13. Дано натуральное число п. Получить все такие натуральные q, при которых п делится на q 2и не делится на q 3.
14. Даны натуральные числа т, п. Получить все их натуральные общие кратные, меньшие тп.
15. Даны целые числа т, п (т≠ 0, n ≠ 0). Получить все их общие делители.
16. Даны действительные числа х, у (x >0, у >1). Получить целое число k (положительное, отрицательное или равное нулю), удовлетворяющее условию yk -1 ≤ x < у k.
17. Дано натуральное число п. Можно ли представить его в виде суммы двух квадратов натуральных чисел? Если можно, то:
а) указать пару х, у таких натуральных чисел, что n = x 2 + y 2;
б) указать все пары х, у таких натуральных чисел, что п = х2 + у2, х ≥ у.
18. Ввести действительное число а. Найти среди чисел 1, 1+ 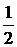 ,
, 
 первое, большее а, вывести это число на экран.
первое, большее а, вывести это число на экран.
19. Ввести действительное число а. Найти такое наименьшее n, что 
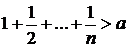 .
.
20. Пусть а 1= b 1 = 1, а k = 3 bk - 1 + 2 ak - 1, bk = 2 а k - 1 + bk - 1, k = 2, 3, …
Ввести натуральное n. Найти 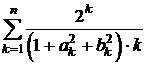 .
.
21. Пусть а 1 = b 1 = 1, 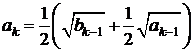 ,
, 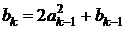 ,
,
k = 2, 3... Ввести натуральное n. Найти  .
.
22. Дано целое число N. Определить первое i, для которого 3 i > N. Значение N ввести в программу. Вывести на экран значения N и i. В процессе отладки программы использовать все команды меню Run, научиться пользоваться окном Watch.
23. Сформировать из введенного числа обратное по порядку входящих в него цифр и вывести на экран. Например, если введено число 3486, то надо вывести число 6843.
24. Среди натуральных чисел, которые были введены, найти наибольшее по сумме цифр. Вывести на экран это число и сумму его цифр.
25. Ввести дату рождения человека (3 числа). Складывать цифры чисел даты рождения, пока не получится однозначное число. Например: 26. 09.2017= 2+6+0+9+2+0+1+7=27=9.
26. Ввести целое число. Найти из каких простых множителей состоит введенное число.
Пояснение к задаче
Чтобы найти все простые сомножители натурального числа, надо его пробовать делить на простые числа, начиная с 2. Если заданное число делится без остатка, значит его делитель - это число, которое входит в состав сомножителей, из которых формируется заданное число. Как только такой сомножитель будет найден, заданное число следует на него разделить, т.е. получить новое заданное число и уже к нему заново подбирать простой делитель. Например, дано число 24. Первое натуральное число, на которое оно делится, - это 2. Значит 2 - это первый простой сомножитель. В результате деления получается 12. Далее снова находим, что 12 делится на 2. Далее 6 делится на 2. Далее 3 делится на 3. Таким образом получаем: 24 = 2 * 2 * 2 * 3.
Поскольку список простых чисел заранее неизвестен, то можно подбирать делители, увеличивая каждый следующий на 1, а не искать простые числа. Ведь если число не делится на 2, то оно не разделится и на 4, 6 и т.д.
27. Найти все совершенные числа до 10000. Совершенное число - это такое число, которое равно сумме всех своих делителей, кроме себя самого. Например, число 6 является совершенным, т.к. кроме себя самого делится на числа 1, 2 и 3, которые в сумме дают 6.
37. Покупатель должен заплатить в кассу х руб. У него имеются купюры по 1, 5, 10, 50, 100, 500, 1000 и 10000 руб. Сколько купюр разного достоинства отдаст покупатель, если он начинает платить с самых крупных купюр?
28. Составить программу, которая печатает таблицу умножения и сложения натуральных чисел в десятичной системе счисления.
29. Составить программу, которая печатает таблицу умножения и сложения натуральных чисел в шестнадцатеричной системе счисления.
30. Найти сумму всех n-значных чисел, кратных k (1 ≤ п ≤ 4). K ввести с клавиатуры
31. Показать, что для всех п = 1, 2, 3, N
(15 + 25 +... + n5) + (17 + 27 +... + n7) = 2(1 + 2 +... + n)4.
Написать программу проверки знания таблицы умножения. Программа должна вывести 10 примеров и выставить оценку: за 10 правильных ответов — "отлично", за 9 и 8 — "хорошо", за 7 и 6 — "удовлетворительно", за 6 и менее — "плохо". Ниже приведен рекомендуемый вид экрана во время работы программы. Ответы пользователя выделены полужирным шрифтом.
*** Проверка знания таблицы умножения ***
После примера введите ответ и нажмите <Enter>.
5x3=15
7x7=49
1x4=4
4x3=12
9x4=36
8x8=64
7x8=52
Вы ошиблись! 7x8=56
4x7=28
3x5=15
2x5=10
Правильных ответов: 9
Оценка: Хорошо.
32. Написать программу проверки умения складывать и вычитать числа в пределах 100. Программа должна вывести 10 примеров, причем в каждом примере уменьшаемое должно быть больше или равно вычитаемому, т. е. не допускается предлагать испытуемому примеры с отрицательным результатом. Оценка выставляется по следующему правилу: за 10 правильных ответов — "отлично", за 9 и 8 — "хорошо", за 7 и 6 — "удовлетворительно", за 6 и менее — "плохо". Ниже приведен рекомендуемый вид экрана во время работы программы. Ответы пользователя выделены полужирным шрифтом.
Проверка умения складывать и вычитать числа.
После примера введите ответ и нажмите <Enter>
75-4=71
35-9=29
Вы ошиблись! 35-9=26
14-1=13
6-5=1
37-19=28
Вы ошиблись! 37-19=18
53-14=39
94-87=7
90-16=74
4-2=2
89-41=48
Правильных ответов: 8
Оценка: Хорошо
33. Составить алгоритм решения ребуса РАДАР = (Р + А + Д)4 (различные буквы обозначают различные цифры, старшая — не 0).
34. Составить алгоритм решения ребуса МУХА + МУХА + МУХА = СЛОН (различные буквы обозначают различные цифры, старшая — не 0).
35. Составить алгоритм решения ребуса ДРУГ — ГУРД = 2727 (различные буквы обозначают различные цифры, старшая — не 0).






