Радиоактивный распад нестабильного ядра – событие случайное, не зависящее от состояния, в котором находятся другие нестабильные ядра. Если нестабильное ядро длительное время не распадалось, то это вовсе не означает, что ему «уже пора»: долгое ненаступление распада не приближает и не отдаляет во времени предстоящий распад. Распад неизбежен, поскольку ядро объективно нестабильное. Вероятность его распада в любую секунду остается величиной постоянной.
Закономерности подобных процессов устанавливаются по средним показателям большой группы ядер, с применением методов математической статистики.
Уравнение радиоактивного распада (Резерфорд, Содди, 1903 год) получено, следуя логике статистического анализа. Эта логика особенно убедительна при записи уравнения распада в дифференциальной форме:
(-dN) / dt = λN (8)
Здесь N – численность нестабильных атомных ядер в момент времени t;
- dN – изменение (уменьшение) этой численности за бесконечно малый
промежуток времени dt наблюдения за распадом;
(-dN) / dt – скорость уменьшения численности нестабильных ядер (скорость
распада в промежутке времени от t до t+dt);
λ – постоянная распада – константа, своя для каждого вида
радиоактивных атомов.
Следовательно, уравнение радиоактивного распада (8) можно сформулировать следующим образом: скорость радиоактивного распада пропорциональна численности еще не распавшихся ядер.
Интегрирование дифференциального уравнения (8) приводит к уравнению радиоактивного распада в интегральной форме:
N = N0 e -l t (9)
Здесь N = N(t) – численность еще не распавшихся ядер как функция времени t;
N0 – численность нераспавшихся ядер в начальный момент времени (при t = 0);
e – основание натуральных логарифмов.
График уравнения (9) представлен на рис. 9:
 |
Рис. 9. График уравнения радиоактивного распада.
Период полураспада – это промежуток времени, в течение которого число нераспавшихся ядер уменьшается в два раза, от N0 до ½N0. Этот показатель связан с постоянной распада следующим образом:
 (10)
(10)
Постоянная распада λ является важной характеристикой радиоактивных ядер: она равна вероятности распада отдельного ядра данного вида за единицу времени. Какая именно единица времени: секунда, минута, или год – будет зависеть от того, в каких единицах времени подставляется в формулу (10) период полураспада Т1/2.
Допустимо и другое толкование: постоянная распада λ равна доле от численности атомных ядер данного вида, распадающихся в единицу времени.
Диапазон значений периода полураспада природных радиоактивных изотопов необычайно широк: от 1,39‧1010 лет для тория 90Th234 до 3,04·10-7 секунды для полония Po212.
Радиоактивные изотопы с периодом полураспада, измеряемые в секундах, минутах, часах и в сутках – это короткоживущие изотопы. Изотопы с периодом полураспада, измеряемым в годах, тысячелетиях, и т.п., -это долгоживущие изотопы.
В медицинской практике нашли применение и те, и другие. Если радиоактивный изотоп вводится в организм, то крайне желательно, чтобы период его полураспада был невелик. Например, хорош изотоп золота 79Au198 с периодом полураспада Т1/2 = 2,7 суток, а изотоп натрия 11Na24 – еще лучше, у него Т1/2=15 часов. Если же пациент подвергается воздействию радиоактивных излучений от внешнего источника, то такой источник удобнее иметь с большим периодом полураспада. Таков, к примеру, изотоп кобальта 27Co60 с периодом полураспада Т1/2 = 5,26 лет. Он излучает b--частицы с энергией 0,31 МэВ и g-кванты 1,33 МэВ и 1,17 МэВ. Кобальтовая пушка – источник g-излучения, применяемый в лучевой терапии.
Активность радиоактивного препарата - это число нестабильных атомов этого препарата, распадающихся за одну секунду. В системе СИ принята единица активности беккерель (в честь Антуана Беккереля, одного из первых исследователей радиоактивности):
1 Бк = 1  = 1 1/c
= 1 1/c
Широко применяется внесистемная единица активности – Кюри:
1 Ки = 3,7×1010 Бк = 3,7×1010 1/c
1Ки – очень большая величина. В медицинской практике используют препараты с активностью в милли- и микрокюри: 1 мКи = 10-3 Ки; 1 мкКи = 10-6 Ки.
Активность, по определению, является показателем скорости распада (число распадов в единицу времени), в то время как в уравнении (9) N – это численность еще не распавшихся ядер. Взяв производную N/ = dN/dt от функции (9), мы получаем уравнение, описывающее активность препарата как функцию времени:
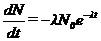 (11)
(11)
Знак «минус» в этом выражении указывает на то, что функция (9) является убывающей, а скорость dN/dt этого убывания уменьшается по экспоненциальному закону, как и численность N в уравнении (9).






