Лабораторная работа должна быть написана чернилами, разборчиво, без помарок и зачеркиваний, на одной стороне листа, с полями левого края не менее 3 см. Все таблицы должны быть составлены с учетом требований (пронумерованы, иметь заголовки и т.д.). Отчет по работе сдается преподавателю для решения вопроса о зачете. Зачет ставится в том случае, если студент: знает назначение работы, порядок ее проведения и умеет анализировать данные, полученные в процессе выполнения работы. В отчете представляется список используемой литературы, где указываются: фамилия и инициалы авторов, название книг, справочников или статей, место издания, издательство или наименование журнала, год издания.
Лабораторная работа №2
«Выборочное наблюдение и его применение на нефтяной и газовой промышленности»
Цель работы
Научиться отбирать исходную информацию путем выборочного наблюдения и переносить результаты выборки на всю генеральную совокупность.
Порядок выполнения работы
1. Выписать исходную информацию по генеральной совокупности в соответствии с номером варианта. Оформить ее в таблицу вида:
Таблица 1
Исходная информация
(название признака)
| Наименование объекта | Значение признака |
| 1. | |
| 2. | |
| 3. | |
| и т.д. |
*) Справочник, таблица
2. Определить численность выборки, исходя из заданного условия выборочного наблюдения.
3. Провести выборку по схеме повторного и без повторного отбора, используя все способы отбора:
- собственно-случайный;
- механический;
- типический;
- гнездовой.
4. Для каждого способа и схемы отбора рассчитать:
- среднее значение признака;
- предельную ошибку;
- предельное значение признака.
5. Вспомогательные расчеты оформить в таблицы вида.
Таблица 2
| №№ объекта | xi | 
| 
|
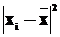
| 1 | |||
| 10 | |||
| 15 | |||
| 16 | |||
| Итого: |
6. Результаты расчетов по всем способам и схемам выборки обобщить в таблице вида. Обобщить результаты расчетов по всем четырем способам в таблице вида
Таблица 3
| Наименование совокупности, способа | Среднее значение | Предельная ошибка | Предельное значение признака | |
| Повторный отбор | Бесповторный | |||
| Генеральная | х | х | ||
| Выборочная | ||||
| - | ||||
| - | ||||
| - | ||||
7. Изобразить графически сопоставления расчетных показателей (сравнение 4-х способов отбора). Сделать вывод, какой из примененных способов отбора наиболее приемлем для данной совокупности.
3. Методика выполнения работы
Способ отбора определяет конкретный механизм или процедуру выборки единиц из генеральной совокупности. Численность выборки определяется или в целом или по группам в зависимости от способа отбора. После определения числа единиц сформировавших выборку, рассчитываются ее характеристики.
1. Собственно-случайная выборка
К собственно-случайной выборке относится отбор единиц из всей генеральной совокупности посредством жеребьевки или какого-либо иного подобного способа, например, с помощью таблиц случайных чисел.
Случайный отбор – это отбор не беспорядочный. Принцип случайности предполагает, что на включение или исключение объекта из выборки не может повлиять какой-либо фактор, кроме случая.
Количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки.
Доля выборки есть отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности 
задано 
и N, то 
Собственно-случайный отбор в чистом виде применяется в практике выборочного наблюдения редко, но он является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного наблюдения.
При случайном повторном отборе средние ошибкирассчитывают:
- для количественного признака
- для альтернативного признака
Поскольку практически дисперсия признака в генеральной совокупности 
точно неизвестна, поэтому используется дисперсия выборочной совокупности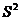 
в соответствии с законом больших чисел, согласно которому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности. Таким образом, средняя ошибка при случайном повторном отборе рассчитывается:
- для количественного признака
- для альтернативного признака
В теории вероятностей доказано, что генеральная дисперсия выражается через выборочную по формуле:
Т.к.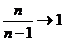 
при достаточном большом значении n, то можно принять 
, т.е. правомерно использовать выше перечисленные формулы.
При малой выборке (если 
) необходимо учитывать коэффициент 
и исчислять среднюю ошибку малой выборки по формуле:
При случайном бесповторном отборе средняя ошибка выборки определяется по формулам:
- для количественного признака
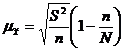
- для альтернативного признака
Т.к. n<N, то 
<1 следовательно, средняя ошибка при бесповторном отборе всегда будет меньше средней ошибки при повторном отборе.
2. Механическая выборка состоит в том, что отбор единиц в выборочную совокупность из генеральной, разбитой по нейтральному признаку на равные интервалы (группы), производится таким образом, что из каждой группы в выборку отбирается лишь одна единица. Чтобы избежать систематической ошибки, отбираться должна единица, которая находится в середине каждой группы.
При организации механического отбора единицы совокупности предварительно располагают в определенном порядке (по алфавиту, местоположению, в порядке возрастания или убывания какого-либо показателя, не связанного с изучаемым свойством и т.д.) после чего отбирают заданное число единиц механически через определенный интервал.
Размер интервала зависит от доли выборки (при 5% выборке отбирается каждая двадцатая единица).
При достаточно большой совокупности механический отбор по точности результатов близок к собственно-случайному. Поэтому для определения средней ошибки механической выборки используют формулы собственно-случайного бесповторного отбора.
3 Типическая выборка
Применяется для отбора единиц из неоднородной совокупности. Она используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, влияющим на изучаемые показатели. При обследовании предприятий такими группами могут быть отрасль и подотрасль, формы собственности. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.
Типическая выборка дает более точные результаты по сравнению с другими способами отбора. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представительство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки.
При определении средней ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.
Средняя ошибка выборки определяется:
– для количественного признака
повторный отбор
бесповторный отбор
– для доли
повторный отбор
бесповторный набор
- средняя из внутригрупповых дисперсий по выборочной совокупности
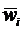- то же самое для доли
4. Серийная выборка
Применение серийной (гнездовой) выборки обусловлено тем, что многие товары упаковываются в пачки, ящики и т.п. для их транспортировки, хранения и сдачи покупателю. В этом случае рациональнее проверить несколько упаковок целиком, чем из каждой упаковки отбирать какое-либо количество единиц.
Поэтому при серийной выборке производится собственно-случайный отбор из генеральной совокупности не отдельных единиц, а групп (серий, гнезд), чтобы в отобранных сериях подвергать наблюдению все единицы. В этом случае средняя ошибка зависит только от межгрупповой дисперсии.
Средняя ошибки при серийной выборке рассчитывается:
– для количественного признака
повторный отбор
бесповторный набор
где: 
– число отобранных гнезд
– общее число гнезд
где: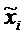 
– средняя в i-ом гнезде
– общая средняя в выборке
– для доли
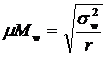повторный отбор
бесповторный набор
где: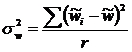 
– доля признака в i-ом гнезде
– общая доля признака в выборке.
На практике применяется каждый рассмотренный способ отбора в отдельности или их комбинация (комбинированный отбор).
Распространение выборочных результатов на генеральную совокупность
Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе выборочных результатов.
Выборочные средние и относительные величины распространяют на генеральную совокупность с учетом предела их возможной ошибки.
В каждой конкретной выборке расхождение между выборочной и генеральной средней 
может быть 
.
Каждое из расхождений имеет различную вероятность (объективную возможность появления событий).
Формула предельной ошибки выборки вытекает из основных положений теории выборочного метода, сформулированного в теории вероятностей через закон больших чисел.
Величина предельной ошибки выборки может быть установлена с определенной вероятностью, значение которой определяется коэффициентом t (на практике заданная вероятность не должна быть меньше 0,95). При t=1 предельная ошибка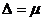 
, т.е. в 68,3% случаев ошибка репрезентативности не выйдет за пределы 
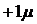, при t=2 с вероятностью 0,954 она не выйдет за пределы 
. Величину 
можно принять за предел возможной ошибки выборки.
Наряду с абсолютным значением предельной ошибки также рассчитывается предельная относительная ошибки:
– для средней 
– для доли 
Определение необходимого объема выборки
При проведении выборочного наблюдения с заранее заданным значением допустимой ошибкой выборки важно правильно определить численность выборки, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения.
Формулы необходимой численности выводят из формул средних ошибок:
– для средней
повторный отбор
– для доли
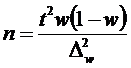повторный отбор
– для средней
бесповторный набор
– для доли
бесповторный набор.
Эти формулы показывают, что с увеличением заданной ошибки значительно уменьшается необходимая численность выборки.
Для расчета численности выборки необходимо знать дисперсию. Она может быть заимствована из расчетов при уже проведенном обследовании.
Выборочный метод широко используется в статистике для получения экономической информации. Большую актуальность он приобрел в условиях становления рыночной экономики. Изменения в характере экономических отношений, аренде, формы собственности обуславливают изменения функции бухучета и статистики, сокращение и упрощение отчетности.
Вместе с тем возрастают требования к менеджменту, что усиливает потребность в обеспечении надежной информации, повышения ее оперативности. Все это обуславливает более широкое применение выборочного метода. Это обследование семей, перепись населения, изучение общественного мнения и т.д.
Выборочный метод основывается на вероятностных совпадениях, что также увеличивает его ценность.
Лабораторная работа №3
«Анализ временных рядов в нефтяной и газовой промышленности»
Цель работы
Научить студентов анализировать динамику показателя, характеризующего рассматриваемое общественное явление и прогнозировать это явление.
Содержание работы
Лабораторная работа состоит из двух взаимосвязанных частей. Эта взаимосвязь выражается в том, что на каждом этапе остается неизменным объект исследования – развитие нефтяной или газовой промышленности.
В первой части рассчитываются показатели, характеризующие динамический ряд, и проводится их анализ.
Во второй части выявляется тенденция динамического ряда с помощью аналитического выравнивания.
Порядок выполнения работы
Часть I. Расчет показателей характеризующих ряд динамики.
1. Выписать исходные данные из приложения в соответствии с порядковым номером в журнале и оформить их в таблицу вида:
Таблица 1
Исходная информация
(наименование показателя)
| Год (ti) | 1 | 2 | 3 | и т.д. | |
| Уровень ряда (yi) |
2. Рассчитать абсолютные и относительные показатели анализа динамического ряда. Расчеты представить в таблице вида:
| Периоды времени (ti) | Уровни ряда (yi) | Абсолютные приросты | Темпы роста, % | Темпы прироста, % | Абсолютный размер 1% прироста | |||
| цеп-ные | базисные | цеп-ные | базисные | цеп-ные | базисные | |||
| Формулы | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| и т.д. | ||||||||
3. Под таблицей выписать расчетные формулы средних величин и рассчитать их.
4. Дать подробную характеристику изменения рассматриваемого показателя за 10 лет.
