Оценка устойчивости капитальной прорези.

Капитальная прорезь обычно оказывается расположенной в границах одной-двух плановых струй. Об устойчивости прорези можно судить, рассчитав начальные деформации дна на площади этих струй. Предварительное качественное заключение об устойчивости прорези можно составить, не прибегая к расчету деформаций, а основываясь только на сведениях о распределении скоростей течения по длинам струй. Для этого расход струи делят на площадь ее поперечного сечения (площадь легко подсчитывается на поперечных сечениях русла с нанесенными на них границами струй). В тех же сечениях вычисляются значения неразмывающей скорости течения. По результатам расчетов строят совмещенные графики изменения скоростей по длине струи v_cp=v_ср(l) и v_нp=v_нр(l) (рис. 4.17, а).

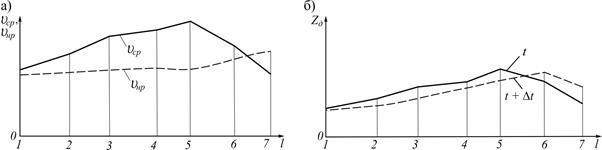
Рис. 4.17. К расчету деформаций дна в плановой струе:

а – график изменения скоростей по длине струи; б – совмещенные продольные профили дна

Если значения скоростей течения в струе больше значений неразмывающей скорости, т.е. v_cp>v_нp, это значит, что по всей длине струи происходит перемещение наносов. Тогда на участках, где скорость течения по длине струи возрастает (дv_cp /дl> 0), должен происходить размыв дна, а на участках, вдоль которых скорость падает (дv_cp /дl< 0), должен идти намыв.

Там, где скорость не изменяется, дно будет оставаться стабильным. Интенсивность деформаций будет тем больше, чем больше превышение скорости течения над неразмывающей скоростью. Если на отдельных участках струи или по всей ее длине скорость течения меньше неразмывающей, т.е. v_cp<v_нp, размыв дна невозможен. Однако здесь могут откладываться наносы, поступающие с вышележащего участка реки во взвешенном состоянии. Поэтому, получив в зоне расположения прорези скорости меньше неразмывающей, следует рассматривать этот результат как свидетельство неустойчивости прорези. Правильно запроектированная прорезь должна «привлекать воду».

Расчет деформаций дна проводится на основе баланса наносов, т.е. путем применения уравнения деформации (2.52). Так как расчет выполняется для фиксированного уровня воды, то входящая во второй член уравнения производная от средней высоты дна по времени может быть заменена взятой со знаком минус производной от средней глубины:

Введя после этого ширину сечения под знак производной, будем иметь уравнение деформации

(4.19)

Уравнение (4.19) решается в конечных разностях. Если t есть начальный момент, а ∆t – выбранный интервал времени, то площадь i -го поперечного сечения плановой струи на момент t + ∆t определяется следующим выражением:

(4.20)

Как видно из уравнения (4.20), приращение площади ω, вызванное деформацией дна, определяется разностью расходов наносов в данном и вышележащем расчетных сечениях струи. Длина ∆l – есть расстояние между этими сечениями: . Разностная схема такого рода называется «левой». Ее применение в расчетах деформаций дна обусловлено тем, что связь между расходом наносов и площадью поперечного сечения обратная. При этом характере связи «левая» схема является устойчивой, а «правая», т.е. использующая вместо сечения l_i-1 сечение l_i+1 – неустойчивой. Интервал времени ∆t берется равным 5-10 сут. Отметка дна в i -м сечении после деформации находится по формуле

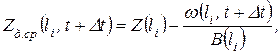(4.21)

где: В – ширина струи.

Разность 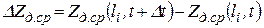выражает деформацию дна в i -м сечении за время ∆t.

Так как расчет делается при уровне воды, равном рабочему уровню дноуглубления, а обычное время разработки капитальных прорезей – межень, то значения расхода Q_s определяются по формулам расхода влекомых наносов, например (2.40) или (2.41). Ввиду малой точности этих формул, получаемые в результате расчетов приращения высоты дна, имеют ориентировочный характер. Однако сравнение их значений на двух участках струи дает вполне достоверное представление о соотношении интенсивности деформаций на этих участках. То же самое следует сказать и о деформациях, полученных для двух вариантов прорези. Если абсолютные значения деформаций могут быть неточными, то отношения этих значений определяются с достаточной надежностью и, следовательно, мы можем иметь правильную количественную оценку того, какова скорость размыва или намыва одной прорези по отношению к скорости размыва или намыва другой.

В целях наглядности результаты расчета деформаций представляют в виде совмещенных продольных профилей дна на моменты времени t и t+∆t. Эти профили удобно помещать на одном рисунке с графиками изменения скоростей (рис. 4.17, б).