1. Расчёт прямозубых и косозубых цилиндрических передач рекомендуется начинать с определения межосевого расстояния после выбора материала зубчатых колёс, расчёта крутящих моментов на валах и назначения передаточного числа передачи, по формуле:
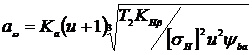, (7.1)
где коэффициент Ка принимается: для прямозубых передач – 49,5
для косозубых передач – 43,0,
u – передаточное число (назначается при разбивке общего передаточного числа редуктора), Т2 – крутящий момент на колесе, Нм,
ƠН – допускаемое контактное напряжение на поверхности зубьев колёс, МПа
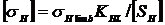. (7.2),
ƠН lim b – выбирается по табл.6.3 для материала шестерни и колеса. Рекомендуется назначать для обоих колёс одинаковый материал, но термообработку шестерни выполнять на 25–30 единиц твёрдости больше по единицам Бринеля, чтобы уравновесить разное количество нагружений зубьев определяемое передаточным числом. После расчёта 
для шестерни и 
для колеса определяется окончательно по формуле: 
. (7.3)
КН L – коэффициент долговечности работы зубчатой пары, рассчитываемый по формуле:
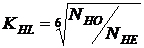, (7.4)
где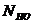 
– базовое число циклов нагружений, принимаемое для стали: 107;
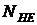– фактическое рассчитываемое число циклов нагружений по заданию проекта (срок службы, коэффициенты работы за год, в смену, в сутки, частота вращения вала).
Если при расчёте колёс из нормализованной или улучшенной стали данный коэффициент получается более 2,6, то он принимается равным 2,6. Для колёс из закаленной стали его максимальное значение КН L равно 1,8. Если в расчётах
КН L получается меньше единицы, то принимается равным единице.
– коэффициент безопасности принимается раным 1,1…1,2 при нормализации или улучшении материала колёс и 
=1,2…1,3 – при закалке.
– коэффициент ширины колеса к межосевому расстоянию, который на начальном этапе проектирования принимается 0,15…0,4.
коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца зубчатого колеса. При проектировании закрытых зубчатых редукторов данный коэффициент выбирается по табл.7.1
Таблица 7.1.
Значения коэффициента KHβ
| Расположение зубчатых колёс относительно опор | Твёрдость поверхности зубьев, НВ | |
| Менее 350 | Более 350 | |
| Симметричное Несимметричное Консольное | 1,00 –1,15 1,10 –1,25 1,2 –1,35 | 1,05 –1,25 1,15 –1,35 1,25 –1,45 |
Примечание. Меньшие значения принимаются при меньших значениях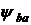 
После вычисления межосевого расстояния 
его необходимо принять по стандартному значению в соответствии с ГОСТ 2185-81:
1-й ряд: 40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400, 500, 630, 800, 1000,..
2-й ряд: 71, 90, 112, 140, 180, 224, 280, 355, 450, 560, 710, 900, 1120,1400,..
Первый ряд следует предпочитать второму.
2. Выбрать модуль зацепления, который принимается в пределах
(0,01– 0,03) 
и приравнять его стандартному значению по ГОСТ 9563-80.
1-й ряд: 1; 1,25; 2; 2,5; 3; 4; 6; 8; 10; 12; 16; 20;
2-й ряд: 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 7; 9; 11; 14; 18; 22.
Первый ряд следует предпочитать второму.
Для косозубых колёс стандартным модулем считается нормальный – mn ..
3. Определить суммарное число зубьев: 
.
Для колёс со стандартным окружным модулем (прямозубых):
. (7.5)
Для косозубых колёс со стандартным нормальным модулем:
, (7.6)
где β – угол наклона зубьев, mt =1/ cos β – торцевой модуль зацепления.
Угол наклона линии зуба принимают для косозубых колёс в интервале
β = 8…150; для шевронных колёс β = 25…400.
4. Определить число зубьев шестерни и колеса:
; 
. (7.7)
Число зубьев округляют в большую сторону до целого и по округлённым значениям уточняют передаточное число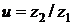 
; и окончательно принимают его по ближайшему стандартному передаточному числу в соответствии с ГОСТ 2185: 1-й ряд: 1; 1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0.
2 -й ряд: 1,12; 1,4; 1,8; 2,24; 2,8; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2.
Первый ряд следует предпочитать второму.
Расхождение с принятым ранее передаточным числом не должно превышать 3%.
После всех указанных округлений необходимо проверить межосевое расстояние – для прямозубых колёс aω = 0,5(z 1 + z 2) mn,
для косозубых колёс aω = 0,5(z 1 + z 2) mn / cos β. (7.8)
При проверке может обнаружиться несоответствие полученного результата с ранее принятым значением aω по стандарту. В этом случае необходимо устранить расхождение изменением угла β:
cos β = 0,5(z 1 + z 2) mn / aω. (7.9)
Вычисление необходимо выполнять с точностью до пяти значащих цифр. Затем рекомендуется проверить расчёты с точностью до сотых долей миллиметра делительных окружностей шестерни и колеса:
d1= z1mn/ cos β. d2= z2mn/ cos β. (7.10)
и убедиться, что принятое ранее aω = 0,5(d 1 + d 2).
5. Далее определяют геометрические параметры передачи:
ширина зучатого колеса b 2 = Ψba aω,
ширина шестерни b 1 = b 2 + (2-8)мм. (в зависимости от габаритов)
диаметры вершин зубьв da 1 = d 1 +2 mn; da 2 = d 2 +2 mn ..
коэффициент шестерни по диаметру Ψbd = b 1 / d 1. (7. 11)
6. Назначение степени точности передачи
Степень точности передачи и коэффициент динамичности КН v назначаются в зависимости от окружной скорости зубчатых колёс v = 0,5 ω 1 d 1 по табл. 7.2
Таблица 7.2.
Значения коэффициента КН v
| Передача | Твёрдость НВ поверхности зубьев | Окружная скорость, м/с. | |||
| До5 | 10 | 15 | 20 | ||
| Степень точности | |||||
| 8 | 7 | ||||
| Прямозубая | Менее 350 | 1,05 | – | – | – |
| Прямозубая | Более 350 | 1,1 | – | – | – |
| Косозубая | Менее 350 | 1,0 | 1,01 | 1,02 | 1,05 |
| Косозубая | Более 350 | 1,0 | 1,05 | 1,07 | 1,1 |
7. Проверка зубчатой передачи на выносливость по контактным напряжениям для прямозубых передач выполняется по формуле:
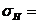
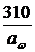
. (7.12)
Для косозубых передач
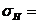
, (7.13)
где: KH =КНβ КН V КН a – коэффициенты нагрузки.
Значения КНβ даны в табл. 7.1, значения КН V даны в табл. 7.2.
Коэффициент КН a учитывает условия монтажа косозубой передачи и в зависимости от окружной скорости зубчатых колёс и степени точности изготовления назначается по табл. 7.3
Таблица 7.3.
Значения коэффициента КН a
| Степень точности | Окружная скорость, м/с | ||||
| до 1 | 5 | 10 | 15 | 20 | |
| 6 | 1 | 1,02 | 1,03 | 1,04 | 1,05 |
| 7 | 1,02 | 1,05 | 1,07 | 1,10 | 1,12 |
| 8 | 1,06 | 1,09 | 1,013 | – | – |
| 9 | 1,1 | 1,16 | – | – | – |
Примечание. Для прямозубых передач КНa =1.
Значения, полученные по формулам (7.12) и (7.13) должны быть меньше значения допускаемого контактного напряжения, вычисленного по формуле (7.3).
В курсовом проектировании допускается перегрузка до 10%.
8. Проверка зубчатой передачи на выносливость по напряжениям изгиба
– (излом зуба) выполняется по формуле:
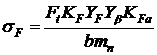, (7.14)
где Ft = 2 T 1 / d 1 = 2 T 2 / d 2 – окружная сила на колесе (Н) (7.15)
К F = KFβ KFv – коэффициент нагрузки, (7.16)
KFβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба, который выбирается по табл. 7.4.
Таблица 7.4.
Значения коэффициента KFβ
| Ψ bd = b / dω 1 | Твёрдость рабочих поверхностей зубьев | |||||||
| Менее 350 НВ | Более 350 НВ | |||||||
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |
| 0,2 | 1,00 | 1,04 | 1,18 | 1,1 | 1,03 | 1,05 | 1,35 | 1,2 |
| 0,4 | 1,03 | 1,07 | 1,37 | 1,21 | 1,07 | 1,1 | 1,7 | 1,45 |
| 0,6 | 1,05 | 1,12 | 1,62 | 1,4 | 1,09 | 1,18 | – | 1,72 |
| 0,8 | 1,08 | 1,17 | – | 1,59 | 1,13 | 1,28 | – | – |
| 1,0 | 1,1 | 1,23 | – | – | 1,2 | 1,4 | – | – |
| 1,2 | 1,13 | 1,3 | – | – | 1,3 | 1,53 | – | – |
| 1,4 | 1,19 | 1,38 | – | – | 1,4 | – | – | – |
| 1,6 | 1,25 | 1,45 | – | – | – | – | – | – |
Примечание. Данные в столбце 1 относятся к симметричному расположению колёс относительно опор; 2 – к несимметричному; 3 – к консольному при установке валов на шарикоподшипниках; 4 – то же, при установке валов на роликоподшипниках.
KFv – коэффициент динамичности, который в зависимости от окружной скорости и термообработки, выбирается по табл. 7.5.
Таблица 7.5.
Значения коэффициента динамичности KFv
| Степень точности | Твёрдость поверхности зубьев,НВ | Окружная скорость, м/с. | ||
| 3 | 3–8 | 8–12,5 | ||
| 6 | менее 350 | 1/1 | 1,2/1 | 1,3/1 |
| 6 | более 350 | 1/1 | 1,15/1 | 1,25/1 |
| 7 | менее 350 | 1,15/1 | 1,35/1 | 1,45/1,2 |
| 7 | более 350 | 1,15/1 | 1,25/1,1 | 1,35/1,1 |
| 8 | менее 350 | 1,25/1,1 | 1,45/1,3 | -/1,4 |
| 8 | более 350 | 1,2/1,1 | 1,35/1,2 | -/1,3 |
Примечание. В числителе указаны значения KFv для прямозубых передач, в знаменателе – для косозубых.
ΥF – коэффициент, учитывающий форму зуба, который в зависимости от числа зубьев, имеет следующие значения:
| z | 17 | 20 | 25 | 30 | 40 | 50 | 60 | 70 | 80 | >100 |
| ΥF | 4,28 | 4,09 | 3,9 | 3,8 | 3,7 | 3,66 | 3,62 | 3,61 | 3,61 | 3,6 |
Для косозубых передач коэффициент формы зуба ΥF следует принимать не по фактическому числу зубьев z, а по эквивалентному zv, которое учитывает повышение несущей способности косозубых передач.
ZV = Z / Cos 3 β (7.17)
Коэффициент Υβ компенсирует погрешности принятой расчётной схемы и при расчёте прямозубых колёс не учитывается:
Υβ =(1- β 0 ) / 140, (7.18)
где β 0 – угол наклона делительной линии зуба.
Коэффициент KFa учитывает неравномерность распределения нагрузки между зубьями и определяется по формуле:
KFa =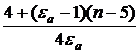 
, (7.19)
где εа – коэффициент торцового перекрытия, n – cтепень точности.
В курсовом проектировании можно принимать среднее значение εа = 1,5 и степень точности 8-ю; тогда KFa = 0,92.
Допускаемое напряжение [ σ F ]при расчёте на изгибную прочность разрешается вычислять по упрощенной формуле:
[ σ F ] = σ 0 Flimb / [ SF ], (7.20)
где коэффициент безопасности [ SF ] = [ SF ]' + [ SF ]''. Первый коэффициент [ SF ]' учитывает нестабильность свойств материала зубчатых колёс (его значения приведены в таблице 7.6). Второй коэффициент [ SF ]''учитывает способ получения заготовки зубчатого колеса: для поковок и штамповок [ SF ]''=1; для проката [ SF ]''=1,15; для литых заготовок [ SF ]''=1,3.
Значения предела выносливости при расчёте на изгибную прочность σ 0 Flimb приведены в таблице 7.6.
Таблица 7.6.
