Способ тестирования ветвей и операторов отношений (автор К. Таи, 1989) обнаруживает ошибки ветвления и операторов отношения в условии, для которого выполняются следующие ограничения [72]:
q все булевы переменные и операторы отношения входят в условие только по одному разу;
q в условии нет общих переменных.
В данном способе используются естественные ограничения условий (ограничения на результат). Для составного условия С, включающего п простых условий, формируется ограничение условия:
ОУс = (d 1, d 2, d 3..... dn),
где d i — ограничение на результат i -го простого условия.
Ограничение на результат фиксирует возможные значения аргумента (переменной) простого условия (если он один) или соотношения между значениями аргументов (если их несколько).
Если i-e простое условие является булевой переменной, то его ограничение на результат состоит из двух значений и имеет вид
di = (true,false).
Если j -е простое условие является выражением отношения, то его ограничение на результат состоит из трех значений и имеет следующий вид:
dj = (>,<,=).
Говорят, что ограничение условия ОУc (для условия С)покрывается выполнением С, если в ходе этого выполнения результат каждого простого условия в С удовлетворяет соответствующему ограничению в ОУc.
На основе ограничения условия ОУ создается ограничивающее множество ОМ, элементы которого являются сочетаниями всех возможных значений d 1, d 2, d 3,..., dn.
Ограничивающее множество — удобный инструмент для записи задания на тестирование, ведь оно составляется из сведений о значениях переменных, которые влияют на значение проверяемого условия. Поясним это на примере. Положим, надо проверить условие, составленное из трех простых условий:
b &(х>у)&а.
Условие принимает истинное значение, если все простые условия истинны. В терминах значений простых условий это соответствует записи
(true, true, true),
а в терминах ограничений на значения аргументов простых условий — записи
(true, >, true).
Ясно, что вторая запись является прямым руководством для написания теста. Она указывает, что переменная b должна иметь истинное значение, значение переменной х должно быть больше значения переменной у, и, наконец, переменная а должна иметь истинное значение.
Итак, каждый элемент ОМ задает отдельный тестовый вариант. Исходные данные тестового варианта должны обеспечить соответствующую комбинацию значений простых условий, а ожидаемый результат равен значению составного условия.
Пример 1. В качестве примера рассмотрим два типовых составных условия:
С& = а & Ь, Сor =а or b,
где а и b — булевы переменные. Соответствующие ограничения условий принимают вид
ОУ & =(d 1, d 2), ОУor=(d 1, d 2),
где d1 = d2 = (true, false).
Ограничивающие множества удобно строить с помощью таблицы истинности (табл. 6.1).
Таблица 6.1. Таблица истинности логических операций
| Вариант | а | b | a & b | a or b |
| 1 | false | false | false | false |
| 2 | false | true | false | true |
| 3 | true | false | false | true |
| 4 | true | true | true | true |
Видим, что таблица задает в ОМ четыре элемента (и соответственно, четыре тестовых варианта). Зададим вопрос — каковы возможности минимизации? Можно ли уменьшить количество элементов в ОМ?
С точки зрения тестирования, нам надо оценивать влияние составного условия на программу. Составное условие может принимать только два значения, но каждое из значений зависит от большого количества простых условий. Стоит задача — избавиться от влияния избыточных сочетаний значений простых условий.
Воспользуемся идеей сокращенной схемы вычисления — элементы выражения вычисляются до тех пор, пока они влияют на значение выражения. При тестировании необходимо выявить ошибки переключения, то есть ошибки из-за булева оператора, оперируя значениями простых условий (булевых переменных). При таком инженерном подходе справедливы следующие выводы:
q для условия типа И (а & b) варианты 2 и 3 поглощают вариант 1. Поэтому ограничивающее множество имеет вид:
ОМ& = {(false, true), (true, false), (true, true)};
q для условия типа ИЛИ (а or b) варианты 2 и 3 поглощают вариант 4. Поэтому ограничивающее множество имеет вид:
ОМor = {(false, false), (false, true), (true, false)}.
Рассмотрим шаги способа тестирования ветвей и операторов отношений.
Для каждого условия в программе выполняются следующие действия:
1) строится ограничение условий ОУ;
2) выявляются ограничения результата по каждому простому условию;
3) строится ограничивающее множество ОМ. Построение выполняется путем подстановки в константные формулы ОМ& или OMOR выявленных ограничений результата;
4) для каждого элемента ОМ разрабатывается тестовый вариант.
Пример 2. Рассмотрим составное условие С 1вида:
В1 &(E 1, E 2),
где В1 — булево выражение, E 1, Е2 — арифметические выражения.
Ограничение составного условия имеет вид
ОУ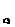 
=(d 1, d 2),
где ограничения простых условий равны
d 1 = (true, false), d 2 = (=, <, >).
Проводя аналогию между С1 и С& (разница лишь в том, что в С1 второе простое условие — это выражение отношения), мы можем построить ограничивающее множество для С1 модификацией
ОМ& = {(false, true), (true, false), (true, true)}.
Заметим, что true для (E 1 = E 2) означает =, a false для (E 1 = E 2) означает или <, или >. Заменяя (true, true) и (false, true), ограничениями (true, =) и (false, =) соответственно, a (true, false) — ограничениями (true, <) и (true, >), получаем ограничивающее множество для С1:
ОМ 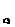= {(false,=),(true,<),(true,>),(true,=)}.
Покрытие этого множества гарантирует обнаружение ошибок булевых операторов и операторов отношения в С1.
Пример 3. Рассмотрим составное условие С2 вида
(E 3 > E 4)&(E 1 = E 2),
где E 1, Е2, Е3, Е4 — арифметические выражения. Ограничение составного условия имеет вид
ОУ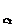 
=(d 1, d 2),
где ограничения простых условий равны
d 1=(=,<,>), d 2 =(=,<,>).
Проводя аналогию между С2 и С1 (разница лишь в том, что в С2 первое простое условие — это выражение отношения), мы можем построить ограничивающее множество для С2 модификацией ОМ :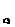
ОМ = {(=, =), (<, =), (>, <),(>, >),(>, =)}.
Покрытие этого ограничивающего множества гарантирует обнаружение ошибок операторов отношения в С2.
