Школьный тур
Класс
1. Торговец купил на оптовом рынке партию ручек и предлагает покупателям либо одну ручку за 10 рублей, либо три ручки за 20 рублей. При этом он в обоих случаях получает одинаковую прибыль (разницу между покупкой товара и его продажей). Какова оптовая цена ручки?
2. В треугольнике ABC угол A равен 40o, угол B равен 20o, а AB - BC = 4. Найдите длину биссектрисы угла C.
3. Найдите сумму двух различных чисел a и b, удовлетворяющих равенству
а ² + в = в ² + а
4. Три ученика A, B и C участвовали в беге на 100 м. Когда A прибежал на финиш, B был позади него на 10 м, также, когда B финишировал, C был позади него на 10 м. На сколько метров на финише A опередил C?
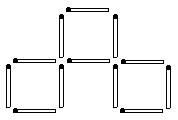
5. Снежная Королева предпочитает идеальные фигуры, поэтому она так любит квадраты. Она дала Каю крест (см. рисунок), чтобы тот разделил его на равные части и собрал из них квадрат. Как это можно сделать?

Математическая олимпиада школьников
Школьный тур
Класс
1. Найдите площадь квадрата, все вершины которого лежат на двух прямых:
x + y = 0 и x+ y = 2.
2. На маленьком острове 2/3 всех мужчин женаты и 3/5 всех женщин замужем. Сколько жителей острова состоят в браке, если всего там проживает 1900 человек?
3. На окружности с диаметром AB и центром O выбрана точка C так, что
биссектриса угла CAB перпендикулярна радиусу OC. В каком отношении
прямая CO делит угол ACB?
4. Найдите количество трехзначных чисел, в десятичной записи которых участвует ровно одна цифра 3.
5. Мама хочет наказать Петю за двойку по математике. Они договорились о
следующем. Петя задумывает двузначное число с разными цифрами
и сообщает его маме. После этого мама называет свое двузначное число
Пете. Петя прибавляет мамино число к своему числу, затем к полученной
сумме, затем к вновь полученной сумме и т.д. до тех пор, пока у него не
получится сумма, оканчивающаяся на две одинаковые цифры. Сможет ли
мама не позволить Пете в этот день поиграть в футбол?
Математическая олимпиада школьников
Школьный тур
Класс
1. Натуральное число n умножили на сумму его цифр и получили 1000. Найдите все такие числа n.
2. При каких значениях параметра a уравнения 2х + a² - 4=0 и 2х² + (а² -4) · х + а =0 будут иметь общий корень? Найдите этот корень.
3. В прямоугольном треугольнике ABC из вершины прямого угла проведена высота CD. Найдите углы треугольника ABC, если известно, что площадь треугольника DBC в 3 раза больше площади треугольника ADC.
4. В школьном турнире по волейболу каждая команда встречается с каждой по одному разу. Перед началом турнира в нем решила принять участие еще одна команда, в результате чего количество встреч, необходимых для проведения турнира, увеличилось на 20%. Сколько команд участвовало в первенстве?
5. Сумма нескольких целых чисел равна 100. Может ли сумма кубов этих чисел равняться 800?
Математическая олимпиада школьников
Школьный тур
Класс
1. Найдите количество четырехзначных чисел, у которых первая цифра в два раза больше последней.
2.
 |
Решите систему уравнений:
3. На велотреке одновременно уходят со старта 5 велосипедистов. Скорость первого равна 50 км/час, второго – 40 км/час, третьего – 30 км/час, четвертого – 20 км/час, пятого – 10 км/час. Первый велосипедист считает количество велосипедистов, которых он обогнал. Какого велосипедиста он посчитал 21-м?
4. В треугольнике ABC проведена высота BD (точка D лежит на стороне AC). Оказалось, что, AB =2 CD и CB =2 AD. Найдите углы треугольника ABC.
5. Три товарища играют друг с другом в настольный теннис по следующему правилу: проигравший отдыхает в следующей партии. Оказалось, что один из них сыграл 21 партию, другой – 10 партий. А сколько партий сыграл третий из них? (Объясните свой ответ).
Ответы и решения 5 класс
1. Ответ: одно из решений: 879 + 426 = 1305.
 |
2.
Ответ. Борис.
В первый и третий день мальчик либо должен был сказать оба раза
правду, либо неправду, так как это дни одной четности. Но в эти дни он
дал разные ответы, значит – сказал неправду. Итак, он сказал правду во
второй день, значит, его зовут Борис.
Ответ. 24 минуты.
Каждые 7 минут гусеница поднимается на 5 ·10 - 2 ·10 =30 см, поэтому за 21 минуту она поднимется на 3 · 30= 90 см. После этого она вновь начинает ползти вверх и за 3 минуты поднимется на оставшиеся 30 см.
Комментарий. Ошибочным является ответ 28 минут, получаемый формальным
подсчетом: (120 см: 30 см) 7 мин, так как он дает второй момент времени, когда гусеница поднимется на высоту 120 см (точнее, в этот момент она спустится до
этого уровня).
5. Ответ: 503 таблетки
Решение: Пока звери не съели лекарство, заберём одну таблетку у носорога, две у бегемота и три у слона. Теперь у всех четверых поровну. Забрали мы 6 таблеток, то есть осталось их 2000 — по 500 у каждого. У слона забрали 3 таблетки, то есть Айболит прописал слону 503 таблетки.
Ответы и решения 6 класс
1. Да. Решение
1 + (2 + 3 + 4). (5 + 6) = 100. Есть и другие решения.
2. Ответ: Синяя ручка, оранжевый карандаш, красный ластик.
Решение
В четвёртом пенале должны лежать предметы, которые уже встречаются в первых трех пеналах, но только по одному разу. Это синяя ручка, оранжевый карандаш и красный ластик.
Ответ. 160 яблок.
Когда из ящика забирается половина яблок, то в нем остается половина от того
количества, которое было перед этим. Значит, перед этим было вдвое больше яблок. Поэтому вначале в ящике было 10х2х2х2х2 = 160 яблок.
4. Ответ: 19 рыжиков и 11 груздей.
Так как среди любых 12 грибов хотя бы один – рыжик, то груздей не больше 11. Так как среди любых 20 грибов хотя бы один – груздь, то рыжиков не больше 19. А так как всего в корзине 30 грибов, то груздей ровно 11, а рыжиков ровно 19.
5. Ответ:
 |  | ||
а) б)
Ответы и решения 7 класс
1. Ответ:
Например, 2 × 2 – 2: 2 = 5 – 5: 5 – 5: 5 или 22: 22 = 55: 5 – 5 – 5.
Или так 2: 2 + 2 + 2 = 5 + 5 –5 + 5 – 5.
2. Ответ: 1760 м.
Решение:
Суммарное расстояние, пройденное паромами к моменту первой встречи, равно ширине реки, а расстояние, пройденное к моменту второй встречи равно утроенной ширине реки. Следовательно, до второй встречи каждый из паромов прошел втрое большее расстояние, чем до первой встречи. Так как один из паромов до первой встречи прошёл 720 м, то до второй встречи он прошёл расстояние 720·3 = 2160 м. При этом он прошёл путь, равный ширине реки, и ещё 400 м. Следовательно, ширина реки равна
2160 − 400 = 1760 м.
3. Ответ: х = 9
Упрощать уравнение необходимо «снаружи», а не изнутри.
4. Ответ: Володя Семенов, Миша Иванов, Петя Герасимов.
Володя учится в 6 классе, а Герасимов в 5 классе, следовательно, Володя не Герасимов; отец Иванова – учитель, отец Володи – инженер, следовательно, Володя не Иванов. Значит, Володя Семенов, Миша Иванов, Петя Герасимов.
5. Ответ: 320 спичек
Решение
Первый способ. Подсчитаем количество треугольников со стороной в одну спичку, у которых спичка в основании расположена горизонтально (см. рис.).

Каждый такой треугольник является верхней половинкой маленького ромбика со стороной в одну спичку. В ромбе со стороной 10 таких ромбиков 10·10 = 100.
Так как никакие два из рассматриваемых треугольников не имеют общих спичек, то на них уйдёт 100·3 = 300 спичек. Если убрать все такие треугольники, то останутся только спички, составляющие две нижние стороны большого ромба. Их – 20, значит, всего потребуется
300 + 20 = 320 спичек.
Второй способ. Ромб со стороной в 10 спичек состоит из 100 маленьких ромбиков. На каждый из маленьких ромбиков уходит 5 спичек, поэтому на 100 ромбиков потребовалось бы 500 спичек, если бы некоторые из спичек не были границей двух ромбиков, а, значит, учтены дважды.
Найдем количество спичек, которые принадлежат только одному ромбику. Это – 40 спичек, образующих контур большого ромба, и 100 спичек, лежащих горизонтально. Следовательно, было 500 – 140 = 360 "двойных" спичек. Таким образом, потребуется 140 + 360: 2 = 320 спичек.
Третий способ. Подсчитаем по отдельности спички, расположенные в каждом из трёх направлений. Параллельно двум сторонам ромба расположено ещё 9 отрезков, каждый из них (включая эти стороны), состоит из десяти спичек, итого: 110 спичек. Ещё 110 спичек лежат параллельно двум другим сторонам ромба. И ещё 100 спичек лежат горизонтально (это видно из предыдущих способов подсчёта, но можно сосчитать и непосредственно:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1).
Ответы и решения 8 класс.
1. Ответ: 5 руб.
Если x – оптовая цена ручки, то при продаже одной за 10 руб. продавец получает прибыль 10 – x (руб.). Продавая три ручки за 20 руб. он получает прибыль 20 – 3 x (руб.). По условию 10 – x = 20 – 3 x, откуда x = 5 (руб.)
2. Ответ: 4
Отложим на стороне AB отрезок BD, равный BC. Тогда треугольник BCD - равнобедренный с углом при вершине 20o, поэтому углы при основании равны 80o (см. рис.). Пусть CE - биссектриса треугольника ABC. Из условия следует, что ACE = 60o, поэтому AEC = 180o - (40o + 60o) = 80o. Таким образом, в треугольнике DEC равны два угла, поэтому он равнобедренный. Тогда угол при его вершине C равен 20o, поэтому ACD = 60o - 20o = 40o. Значит, треугольник ACD также равнобедренный, следовательно, CE = CD = AD = AB - BC = 4.
 |
3. Ответ: 1
Преобразуем данное равенство: a² – b² - (a- b) = 0 или (a - b)(a+ b - 1)= 0. По
условию данные числа различны. Поэтому первая скобка не равна нулю. Значит,
a +b - 1 =0, откуда a+ b = 1.
Ответ. На 19 м.
Из условия следует, что скорость ученика B составляет 0,9 от скорости ученика A, а скорость ученика C составляет 0,9 от скорости ученика B. Из этого следует, что скорость ученика C составляет 0,81 от скорости ученика A. Значит, когда A пробежит 100 м, ученик C пробежит 81 м.
5. Ответ. Пусть длина каждой стороны креста равна 1. Тогда необходимо так разрезать крест на части, чтобы из этих частей можно было собрать квадрат площади 5.
Соединим середины противоположных сторон, как на рисунке. Из четырех полученных фигур сложим искомый квадрат.

Ответы и решения 9 класс
Ответ. 2.
Длина стороны этого квадрата – расстояние между прямыми x + y = 0 и
x + y = 2, так как на каждой из прямых – по две вершины квадрата. А это расстояние равно расстоянию от начала координат до прямой x + y = 2, пересекающей оси координат на расстоянии 2 от начала координат. Значит, искомое расстояние – высота в равнобедренном прямоугольном треугольнике с катетами длины 2, которая равна √2.
Ответ. 1200 человек.
Пусть x – количество мужчин, y – количество женщин на этом острове. Из условия следует, что 2/3 х = 3/5 у, кроме того, х + у = 1900.
Решая эту систему, получаем: x = 900, y = 1000. Отсюда количество женатых мужчин равно 2/3 ∙ 900= 600, а общее количество людей, состоящих в браке, равно 1200.
3. Ответ: 2: 1
Биссектриса угла CAO является высотой треугольника CAO, поэтому
CA = AO. Но OA = OC – как радиусы, значит, треугольник CAO – равносторонний. Тогда угол ACO = 60º. Кроме того, в равнобедренном треугольнике OCB (OC = OB) угол COB = 120º, поэтому угол OCB = 30º (иначе это можно получить, воспользовавшись тем, что угол ACB – опирающийся на диаметр, равен 90º).
Ответ. 225.
Если у трехзначного числа на первом месте стоит цифра 3, то две другие цифры – произвольные, отличные от 3. Значит, на втором месте может стоять любая из 9 других цифр, и на третьем – любая из 9 других цифр – всего 9х9 = 81 вариант. Если тройка стоит на втором месте, то на первом месте может стоять любая цифра, кроме 3 и 0, а на последнем – любая, кроме тройки. Всего получается 8х9 = 72 варианта. Столько же вариантов мы получим, если тройка будет стоять на последнем месте. Итого: 81 + 72 + 72 = 225 вариантов.
Ответ. Сможет.
Если Петя задумает число с двумя цифрами разной четности, то маме нужно назвать, например, число 20. Тогда четность каждой из двух последних цифр после каждого прибавления будет сохраняться, и эти цифры никогда не совпадут. Если же цифры Петиного числа будут одной четности, то маме достаточно назвать число 50. После каждых двух прибавлений последние две цифры будут повторяться, т.е. не будут совпадать, а после первого (третьего, пятого и т.д.) прибавления эти цифры будут иметь разную четность, т.е. тоже не совпадут.
Ответы и решения 10 класс.
Ответ. 125 и 1000.
Решение: Раскладывая 1000 в произведение двух множителей: 1000х1, 500х2, 250х4, 200х5, 125х8, 100х10, 50х20, 40х25 мы получаем два варианта ответа.
2. Ответ. а = 0, x = 2.
Если x – корень уравнения 2 х + а² - 4 =0 , то он также и корень уравнения х (2 x+ a ² - 4) = 0, то есть 2 x ² + (a ² - 4) x = 0. Кроме того, по условию, x – корень уравнения 2 x ² + (a ² - 4) x + a= 0. Значит x – корень уравнения (2 x ² + (a ² -4) x+ a) – (2 x ²+ (a ² – 4) x) = 0, то есть a= 0 Осталось проверить, что при таких a оба уравнения имеют общий корень x = 2.
3. Ответ. Угол CAB = 60 º, угол CBA = 30 º.
Заметим, что треугольник CBD подобен треугольнику ACD (свойство высоты прямоугольного треугольника). Но в подобных треугольниках отношение площадей равно квадрату отношения соответственных сторон. Поэтому отношение гипотенуз CB и CA этих треугольников равно √3. Значит, tg CAB= √ 3, откуда угол CAB = 60º.






