Рассмотрим нечеткие ориентированные графы. Они также, как и нечеткие неориентированные графы могут быть двух видов. К первому виду относят графы, имеющие нечеткое множество ребер. Ко второму виду относят графы, имеющие, кроме того, нечеткое множество вершин.
Зададим нечеткий ориентированный граф первого рода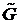 
= (X, 
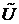). При этом X = { xi }, i Î I = {1, 2,..., n }, а 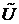= {< m U< х i, х k >/< х i, х k >>},< х i, х k > Î Х2, m U< х i, х k > – степень принадлежности ориентированного ребра < х i, х k > нечеткому множеству ориентированных ребер .
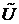Нечеткий ориентированный граф первого рода можно также удобно задавать в виде 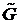= (Х,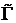 
), где X = { xi }, i Î I = {1, 2,..., n }, а 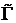- нечеткое многозначное отображение множества вершин X в себя, т.е. 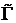: X → X, задаваемое в виде системы нечетких образов элементов x Î X при этом отображении, т.е. 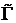(xi) = {< m Г (xj)/ xj >}, xj Î Г(xi), здесь Г(xi) - четкое множество образов вершины xi Î X.
Как нечеткий неориентированный, так и ориентированный графы удобно задавать в виде нечетких матриц смежности R x = || rik || n, где rik = m U(х i, х k) для неориентированных графов и m U< х i, х k > для ориентированных графов.
Нечетким ориентированным графом второго вида называется граф = (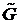
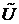, ), где – множество вершин является нечетким множеством в некотором универсальном множестве А, т.е. = {< m x (x)/ x >}, x Î А, | | = n, 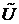– нечеткое множество ориентированных ребер определяется как 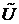= {< m U< х i, х k >/< х i, х k >>}, < х i, х k > Î X2, где X – носитель множества .
Нечеткий ориентированный граф второго вида 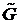= (, 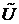) при необходимости можно однозначно преобразовать в нечеткий ориентированный граф первого вида G' = (X, 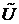') следующим образом. В качестве множества вершин X принимается носитель множества , а нечеткое множество ориентированных ребер 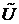' принимает вид: 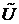' = {< m U'< х i, х k >/< х i, х k >>}, < х i, х k > Î X2, где функция m U'< х i, х k > = m U< х i, х k > & m X(х i) & m X(х k), в минимаксном базисе – m U'< х i, х k > = min(m U< х i, х k >, m X(х i), m X(х k)), и в вероятностном базисе – m U'< х i, х k > = m U< х i, х k > ´ m X(х i) ´ m X(х k). Графы 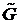и G' будем называть сопряженными.
Каждому ориентированному нечеткому графу второго вида соответствует единственный ориентированный нечеткий граф первого вида, в то же время каждому ориентированному нечеткому графу первого вида соответствует бесконечно много нечетких графов второго вида.
Аналогичные преобразования можно выполнить и для преобразования нечеткого неориентированного графа второго вида к нечеткому неориентированному графу первого вида.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Пусть задан орграф D, изображенный на рис. 17.21, а. Построить основание, матрицу смежности и матрицу инцидентности заданного графа.
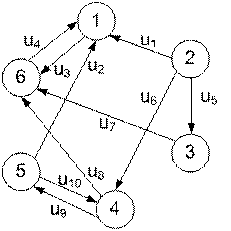
Рис. 17.21, а. Ориентированный граф D
Решение: основание исходного графа D, полученное путем замены дуг соответствующими им ребрами, показано на рис. 17.21, б.
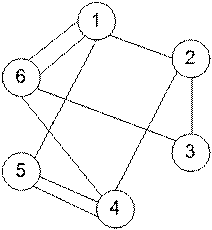
Рис. 17.21, б. Основание графа D
Матрица смежности исходного графа D будет иметь следующий вид:
| 1 | 2 | 3 | 4 | 5 | 6 | r +(xj) | . | ||
| R(D) = | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 2 | 1 | 0 | 1 | 1 | 0 | 0 | 3 | ||
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | |||
| 4 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | ||
| 5 | 1 | 0 | 0 | 1 | 0 | 0 | 2 | ||
| 6 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| r –(xj) | 3 | 0 | 1 | 2 | 1 | 3 |
Таким образом, для вершины x 1, например, полустепень исхода r +(x 1) равна единице, а полустепень захода r –(x 1) равна трем.
Матрица инцидентности для того же графа запишется следующим образом:
| u 1 | u 2 | u 3 | u 4 | u 5 | u 6 | u 7 | u 8 | u 9 | u 10 | |||
| I(D) = | х 1 | – 1 | – 1 | + 1 | – 1 | 0 | 0 | 0 | 0 | 0 | 0 | . |
| x 2 | + 1 | 0 | 0 | 0 | + 1 | + 1 | 0 | 0 | 0 | 0 | ||
| х 3 | 0 | 0 | 0 | 0 | – 1 | 0 | + 1 | 0 | 0 | 0 | ||
| x 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | + 1 | + 1 | – 1 | ||
| x 5 | 0 | + 1 | 0 | 0 | 0 | 0 | 0 | 0 | – 1 | + 1 | ||
| x 6 | 0 | 0 | – 1 | + 1 | 0 | 0 | – 1 | – 1 | 0 | 0 |
Пример 2. Пусть задан ориентированный граф D = (X, U) (рис. 17.22). Построить дерево, используя вышеописанный алгоритм.
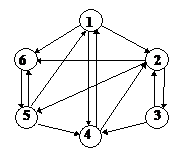
Рис. 17.22. Орграф D
Решение: 1. Выбираем вершину x 1. Находим смежные ей вершины и получаем подмножество X’ = { x 1, x 2, x 4, x 6}. Поскольку êX’ï ¹ X, переходим к пункту 2.
2. Из подмножества X’ выбираем произвольную вершину, например x 2. Находим смежные ей вершины. Это вершины x 3, x 5, x 6. Добавляем в подмножество X’ вершины x 3, x 5. Вершина х 6 уже входит в подмножество X’, поэтому дугу < x 2, x 6> мы игнорируем.
3. После выполнения пункта 2 настоящего алгоритма получим подмножество X’ = { x 1, x 2, x 3, x 4, x 5, x 6}, таким образом, условие êX’ï = êХï, выполнено, переходим к пункту 4.
4. Построено дерево Т = {< x 1, x 2>, < x 1, x 4>, < x 1, x 6>, < x 2, x 3>, < x 2, x 5>}. Алгоритм окончен.
Ответ: Построено дерево Т (рис. 17.23.).
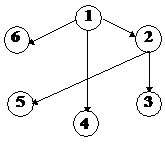
Рис. 17.23. Дерево T
Пример 3. Разбить граф G = (X,U), изображенный на рис. 17.24, на максимально связные подграфы и построить его конденсацию.
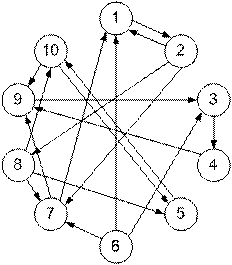
Рис. 17.24. Граф G
Решение: Используем алгоритм Мальгранжа.
Выбираем произвольную вершину. Пусть это будет вершина х 1. Строим матрицу смежности заданного графа.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| R = | 1 | 1 | |||||||||
| 2 | 1 | 1 | 1 | ||||||||
| 3 | 1 | ||||||||||
| 4 | 1 | ||||||||||
| 5 | 1 | ||||||||||
| 6 | 1 | 1 | 1 | ||||||||
| 7 | 1 | 1 | |||||||||
| 8 | 1 | 1 | 1 | ||||||||
| 9 | 1 | ||||||||||
| 10 | 1 | 1 |
По матрице смежности определяем вершины, достижимые из вершины х 1:
Г+(x 1) = { х 1} È { х 2}.
Теперь определяем вершины, достижимые из х2:
Г+(x 1) = { х 1} È { х 2} È { х 1, х 7, х 8}.
Определяем вершины, достижимые из х7 и х8:
Г+(x 1) = { х 1} È { х 2} È { х 1, х 7, х 8} È { х 1, х 9, х 5, х 7, х 10}.
Определяем вершины, достижимые из вершин х 5, х 9, х 10:
Г+(x 1) = { x 1} È { x 2} È { x 1, х 7, х 8} È { х 1, х 5, х 7, х 9, х 10} È { х 3, х 5, х 9, х 10}.
Определяем вершины, достижимые из вершины х 3:
Г+(x 1) = { х 1} È { х 2} È { х 1, х 7, х 8} È { х 2, х 5, х 7, х 9, х 10} È { х 3, х 5, х 9, х 10} È { х 4}.
Поскольку из вершины х 4 достижима только вершина х 9, а она уже включена в список рассмотренных вершин, то в итоге, после выполнения операции объединения данных подмножеств вершин, получим Г+(x 1) = { х 1, х 2, х 3, х 4, х 5, х 7, х 8, х 9, х 10}.
Теперь нам необходимо найти вершины, из которых достижима вершина х 1:
Г -(x 1) = { х 1} È { х 2, х 6, х 7} È { х 1} È { х 2, х 6, х 8} È { х 2} = { х 1, х 2, х 6, х 7, х 8}.
Теперь для того, чтобы выделить максимально связную компоненту, нам необходимо найти пересечение данных множеств:
Г+(х 1) Ç Г-(х 1) = { х 1, х 2, х 7, х 8}; Х1* = { х 1, х 2, х 7, х 8}.
Исключаем эти вершины из рассмотрения и продолжаем процесс выделения максимально связных компонент. Берем вершину х 3 и определяем для нее прямое и обратное транзитивное замыкание:
Г+(x 3) = { x 3} È { x 4} È { x 9} È { x 3} = { x 3, x 4, x 9};
Г -(x 3) = { x 3} È { x 6, x 9} È { x 4, x 10} È { x 3, x 5} È { x 10} = { x 3, x 4, x 5, x 6, x 9, x 10}.
Тогда сильная компонента:
Х2* = Г+(x 3) Ç Г -(x 3) = { x 3, x 4, x 9}.
Продолжаем процесс. Выбираем из оставшихся вершин х 5, х 6, х 10 вершину х 5:
Г+(x 5) = { x 5} È { x 10} È { x 5} = { x 5, x 10};
Г -(x 5) = { x 5} È { x 10} È { x 5} = { x 5, x 10}.
Таким образом, получена сильная компонента:
Х3* = { x 5, x 10}.
У нас осталась всего одна невыделенная вершина - это вершина х 6. Следовательно, вершина х 6 образует последнюю сильную компоненту в графе G: X4* = { x 6}.
Итак, мы выделили в заданном графе все возможные сильные компоненты.
Теперь строим конденсацию графа G. В качестве вершин графа конденсации выступают сильные компоненты, при этом вершины, составляющие каждую сильную компоненту, стягиваются в одну. Все ребра, соединяющие стягиваемые вершины с вершинами, принадлежащими другим сильным компонентам, сохраняются. Таким образом, мы построили конденсацию D* (рис. 17.25) исходного графа G.
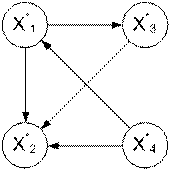
Рис. 17.25. Конденсация D*
Пример 4. Для графа D = (X, U) на рис. 17.26 определить прямое и обратное транзитивные замыкания для вершины х 7.
Решение:
Г+ х 7 = { х 7} È Г+ х 7 È Г+2 х 7 È Г+3 х 7;
Г+ х 7 = { х 7, х 4, х 6};
Г+2 х 7 = Г+{Г+ х 7} = Г+{ х 7, х 4, х 6} = { х 7, х 4, х 6, х 2, х 5};
Г+3 х 7 = Г+{Г+2 х 7} =Г+{ х 7, х 4, х 6, х 2, х 5} = { х 7, х 6, х 4, х 5, х 1, х 2, х 3};
Г– х 7 = { х 7} È Г–1 х 7 È Г–2 х 7;
Г– х 7 = { х 7, х 2};
Г–2 х 7 = Г–{Г– х 7} = { х 7, х 2, х 4};
тогда Г– х 7 = { х 2, х 4, х 7};
а Г х 7 = { х 1, х 2, х 3, х 4, х 5, х 6, х 7} = Х.
Пример 5. Построить разбиение на основе метода Мальгранжа ориентированного графа D = (X, U), заданного матрицей смежности R.
| х 1 | х 2 | х 3 | х 4 | х 5 | х 6 | х 7 | Г+ х 1 | . | |||
| R = | х 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ||
| х 2 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | – | |||
| х 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |||
| х 4 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | – | |||
| х 5 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | – | |||
| х 6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | – | |||
| х 7 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | – | |||
| Г– х 1 | 0 | 1 | 1 | 2 | 2 | 3 | 3 |
Решение: Столбец Г+ х 1 строится следующим образом. В клетке столбца против стрелки х 1 ставится 0. В клетку столбца против строки х 3 ставится 1, так как строка х 1 содержит 1 на месте х 3. Строка х 3 содержит 1 только на уже отмеченном месте х 1. Тогда в оставшиеся клетки столбца Г+ х 1 проставляются знаки «–». Числа в клетках Г+ х 1 — это количество путей из вершины х 1 в другие вершины графа D. Тогда Г+ х 1 = { х 1, х 3}.
Аналогично заполняются клетки строки Г– х 1. Против столбца х 1 в клетке Г– х 1 ставится 0. В клетках строки Г– х 1 против х 2 и х 3 ставится 1, так как столбец имеет 1 против х 2 и х 3. В столбце х 2 имеется 1 против строки х 4, следовательно, в клетку Г– х 1 против х 4 записывается 2. В столбце х 3 имеем единицы против строк х 1 и х 5. Строка х 1 уже рассмотрена, а в клетке Г– х 1, расположенной против х 5, ставится 2. Далее аналогично заполняются оставшиеся клетки Г– х 1. Тогда Г– х 1 = { х 1, х 2, х 3, х 5, х 6, х 7}, С(х 1) = Г+ х 1 Ç Г– х 1 = { х 1, х 3}. Теперь удалим из графа D вершины х 1 и х 3. Получим матрицу R' оставшегося графа D'.
| х 2 | х 4 | х 5 | х 6 | х 7 | Г+ х 2 | . | |||
| R' = | х 2 | 0 | 0 | 0 | 0 | 1 | 0 | ||
| х 4 | 1 | 1 | 0 | 0 | 0 | 2 | |||
| х 5 | 0 | 0 | 0 | 1 | 0 | 3 | |||
| х 6 | 0 | 0 | 1 | 0 | 0 | 2 | |||
| х 7 | 0 | 1 | 0 | 1 | 1 | 1 | |||
| Г– х 2 | 0 | 1 | – | – | 2 |
Аналогично, заполняя клетки Г+ х 2 и Г– х 2, определяем Г+ х 2 = { х 2, х 4, х 5, х 6, х 7}, Г– х 2 = { х 2, х 4, х 7}. Тогда С(х 2) = Г+ х 2 Ç Г– х 2 = { х 2, х 4, х 7}. Снова удалим из D' вершины х 2, х 4, х 7, получим граф D". Запишем его матрицу смежности.
| х 5 | х 6 | Г+ х 5 | . | |||
| R'' = | х 5 | 0 | 1 | 0 | ||
| х 6 | 1 | 0 | 1 | |||
| Г– х 5 | 0 | 1 |
Получим Г+ х 5 = { х 5, х 6}, Г– х 5 = { х 5, х 6}, C(х 5) = { х 5, х 6}. Следовательно, в результате работы алгоритма получили разложение графа на три части, показанные на рис. 17.26 штриховыми линиями.
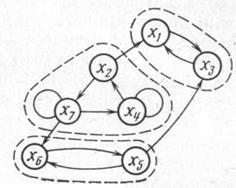
Рис. 17.26. Разложение графа на максимально связные подграфы
Пример 6. Зададим нечеткий ориентированный граф первого рода 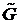= (X, 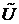), где X = { х 1, х 2, х 3, х 4, х 5}, а 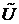= {<1/< х 1, х 4>>, <0,5/< х 1, х 5>>, <0,1/< х 2, х 2>>, <0,9/< х 2, х 3>>, <0,8/< х 4, х 2>>, <0,2/< х 4, х 1>>, <0,6/< х 5, х 5>>}.
Граф 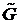показан на рис. 17.28.
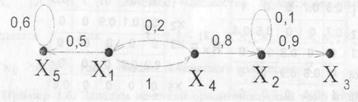
Рис. 17.28. Нечеткий ориентированный граф первого рода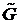
Пример 7. Зададим нечеткий граф из примера 1 в виде 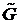= (Х, ).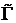
Решение: Получим X = { х 1, х 2, х 3, х 4, х 5}, 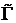(x 1) = {<1/ х 4>,<0,5/ х 5>}, 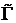(x 2) = {<0,1/ х 2>,<0,9/ х 3>}, 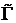(x 3) = Æ, 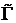(x 4) = {<0,2/ x 1>, <0,8/ х 2>}, 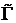(x 5) = {<0,6/ х 5>}.
Пример 8. Записать матрицу смежности R x 2 графа, рассмотренного в примере 1.
Решение: Матрица смежности запишется следующим образом:
| x 1 | x 2 | x 3 | x 4 | x 5 | |||
| R x 2 = | x 1 | 0 | 0 | 0 | 1 | 0,5 | . |
| x 2 | 0 | 0,1 | 0,9 | 0 | 0 | ||
| x 3 | 0 | 0 | 0 | 0 | 0 | ||
| x 4 | 0,2 | 0,8 | 0 | 0 | 0 | ||
| x 5 | 0 | 0 | 0 | 0 | 0,6 |
Пример 9. Задать нечеткий ориентированный граф второго вида 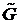= (, 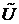), = {<0,9/ x 1>, <0,8/ х 2>, <0,7/ х 3>, <0,6/ x 4>, 0,4/ х 5>}, 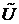= {<0,4/< x 1, х 2>>, <0,8/< x 1, х 3>>, <1/< x 1, x 4>>, <0,5/< х 3, x 4>>, <0,9/< х 3, х 5>>}.
Решение: Граф 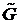= (, 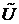) приведен на рис.17.29.
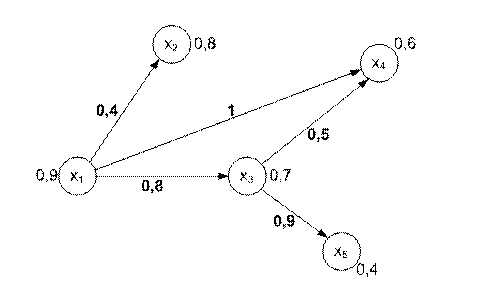
Рис. 17.29. Нечеткий ориентированный граф второго вида = (, )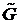
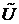ВОПРОСЫ
1. Дайте определение ориентированного графа.
2. Что понимается под достижимостью?
3. Что такое основание орграфа?
4. Что называется сильной компонентой орграфа?
5. Поясните принцип формирования матриц достижимости и контрдостижимости.
6. В каком случае говорят, что вершины орграфа взаимнодостижимы?
7. Как определяется прямое и обратное транзитивное замыкания?
8. Что такое конденсация графа?
9. Опишите алгоритм разбиения графа на максимально связные подграфы.
10. Определите полустепени исхода и захода.
