СТІЙКІСТЬ АВТОМАТИЧНИХ СИСТЕМ КЕРУВАННЯ
План
1. Стійкістьлінійних систем автоматичного керування.
2. Алгебраїчнікритерії стійкості.
3. Частотнікритеріїстійкості.
Стійкістьлінійних систем автоматичного керування.
Точністьвиконаннятехнологічногопроцесузалежитьвідроботоздатності АСК, щовизначаєтьсяїїстійкістю.
При прикладені до АСК будь-якої дії її рух може бути різним, але з умов стійкості роботи він буде стійким, не стійким і на межі стійкості.
АСК є стійкою, якщо вона повертається до усталеного режиму, післяприпиненнядіїзбурення, щовивелоїї з цього стану.
Нестійка система не повертається до усталеного стану рівноваги, з якого вона вийшла. Вихідна величина такоїсистемибезперервнозбільшуєтьсяабоздійснюєнедопустимівеликіколивання.
О.М.Ляпуновзапропонувавоцінюватистійкістьсистеми на основіаналізурівняннядинаміки, щоописує систему.
Рівняння системи в період Т характеризується диференційним рівнянням при x (t)=0, тобто однорідним рівнянням (із сталими коефіцієнтами):
В операторнійформі
Загальнимрозв’язкомданогодиференційногорівняння буде:
де l i – корені характеристичного рівняння;
ci – стала, щовизначаєтьсяпочатковимиумовами.
Кореніможуть бути дійсними та комплексними.
 |
Аналізотриманогорішенняпоказує, що
- при l = - a (негативнийкорінь) – процесзатухає (крива 1) – стійка система;
- при l = a (позитивнийкорінь) – процесрозходиться (крива 2) – система нестійка;
- при l = 0 –процес не змінюєсвого стану (лінія 3) – система знаходиться на межістійкості.
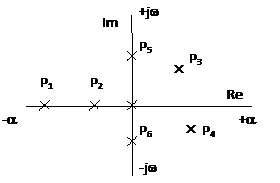
При одержанікомплекснихкоренів: l = ± a ± j w (y (t)= ce a t sin (w t + j)
- l = -a± j w- затухаючіколивання (крива 1) – система стійка;
- l = a± j w- коливаннярозходяться (крива 2) – система нестійка;
- l = ± j w- коливання з сталоюамплітудою, не затухають (крива 3) – система на межістійкості.
 |
В загальномувипадку:
стійка – кореніповинні бути від’ємними, а комплекснікоренімали б від’ємнудійснучастину;
нестійка – хоча б один корінь буде позитивний;
на межістійкості – при наявностінульовогокореняабо пари чисто умовнихкоренів, що лежать на умовнійвісі.
Труднощівиникають при розв’язуванніхарактеристичнихрівняньвисокихпорядків (при n > 4), тому булирозроблено ряд принципів, що дозволили визначитистійкістьавтоматичних систем не обчислюючикоренів характеристичного рівняння. Ціпринципиназиваютьсякритеріямистійкості.
Алгебраїчні критерії стійкості.
Критеріїстійкості - це математичнаформуліровка умов, якимзадовольняютькоефіцієнти характеристичного рівняннясистеми автоматичного керування.
Існуєдекількакритеріїв, але з математичної точки зорувонивсіеквівалентні.
Всікритеріїподіляються на двігрупи:
- алгебраїчні;
- частотні.
Алгебраїчнікритеріївизначаютьсукупністьалгебраїчнихнерівностей, щоописуютьзв’язкиміжкоефіцієнтами характеристичного рівняннясистеми.
КритерійРауса (1877р.)
Хай є характеристичнерівняннясистеми:
Складаєтьсятаблиця (матриця) Рауса:
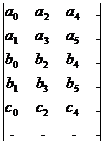
Число строчок матрицідорівнює n+1.
Коефіцієнтиутворюються за наступним правилом:
а0; а1; а2 ... ап – коефіцієнти характеристичного рівняння.
b 0 = а2 - а0 а3/ а1 = а2 - l 1 а3; b 2 = а4 - l 1 а5 і т.д.
b 1 = а3 – а1 b 0 / b 2 = а3 - l 2 b 2; b 3 = а5 - l 2 b 4; b 5 = а7 – l 2 b 6 і т.д.
с0= b 2 - b 0 b 3 / b 1 і т.д.
Критерійформулюється таким чином: для стійкостісистеминеобхідно і достатньо, щобкоефіцієнтипершогостовпчикатаблицібулипозитивними.
Приклад:
4р4 + 7р3 + 5р2 + 3р + 1 = 0
кількість строчок п+1=4+1=5
b0=5-4×3/7=23/7; b2=1-4×0/7=1; b1=3-7×1/23/7=20/23; b3= 0-0×49/23=0; C0 =1- 0×23/7 / 20/23=1
Дана система стійка.
КритерійГурвіца (1895р.)
Базується на визначенні табличного записукоефіцієнтів характеристичного рівняння:
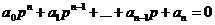
і формулюєумовустійкості в залежностівідзнаківвизначників.
ВизначникГурвіцаскладається таким чином: коефіцієнтивід а1 до ап розташовуються за головною діагоналею в порядку зростання. Вверх відголовноїдіагоналі в стовпчикахзаписуютькоефіцієнти з послідовнозростаючимиіндексами, а вниз – з індексами, щозменшуються. На місцяхкоефіцієнти, індексияких > n та < 0 проставляють 0.
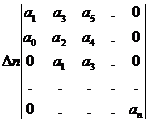
Критерійвстановлює, що система стійкатоді та тількитоді, коли всідіагональнімінорибільше нуля, тобтоспівпадають за знаком з першим коефіцієнтом а0.
D 0 =а0 > 0; D 1 =а1 > 0; 
; 
;...
D п > 0.
Приклад:
р5 +3р4 + 5р3 + 7р2 + 2р + 2 = 0
а0 = 1 > 0; D1=3> 0; 
; 
D5=2D4=32> 0.
Система стійка.
КритерійГурвіцазастосовують для рівнянь до п’ятого порядку.
ПорівняннякритеріївРауса та Гурвіцапоказує,що перший маєалгоритмічний характер (елементиз’являються в результатірозрахунку), а другий – замкнуту форму. РанішечастішевикористовувавсякритерійГурвіца. Зпоявоюцифровихобчислювальних машин, для лінійних систем високого порядку, застосовуютькритерійРауса.
