Ф.1 Модуль линейной деформации 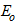 и коэффициент нелинейной деформации
и коэффициент нелинейной деформации  определяют по зависимости, устанавливающей связь между относительными продольными деформациями
определяют по зависимости, устанавливающей связь между относительными продольными деформациями 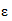 , напряжениями
, напряжениями 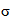 и временем действия нагрузки t
и временем действия нагрузки t
 , (Ф.1)
, (Ф.1)
где  - функция напряжений
- функция напряжений 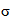 для времени
для времени 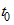 их действия, равного 1 ч,
их действия, равного 1 ч, 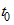 которую принимают в виде:
которую принимают в виде:
 - для модели линейно деформируемого основания;
- для модели линейно деформируемого основания;
 - для модели нелинейно деформируемого основания,
- для модели нелинейно деформируемого основания,
где 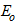 и
и  - параметры функции
- параметры функции  ;
;
m - коэффициент нелинейности по напряжениям.
Ф.2 Предельно длительные значения Е и А вычисляют по формулам:
 ; (Ф.2)
; (Ф.2)
 , (Ф.3)
, (Ф.3)
где  - время, равное сроку службы сооружения, или принимаемое равным 50 лет =
- время, равное сроку службы сооружения, или принимаемое равным 50 лет =  ч;
ч;
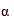 - коэффициент нелинейности во времени.
- коэффициент нелинейности во времени.
Ф.3 Для установления зависимости (Ф.1) исходные данные испытаний (см. 6.3.5) обрабатывают в соответствии с теорией наследственной ползучести. Используя кривую ползучести (см. 6.3.5.7), последовательно вычисляют ряд значений  , имеющих смысл деформаций, которые развились бы под действием постоянного напряжения (i=1, 2,...), соответствующего напряжению i-й ступени нагружения, за время
, имеющих смысл деформаций, которые развились бы под действием постоянного напряжения (i=1, 2,...), соответствующего напряжению i-й ступени нагружения, за время  . Вычисления проводят по формуле
. Вычисления проводят по формуле
 , (Ф.4)
, (Ф.4)
где  - полная относительная продольная деформация предшествующей ступени нагружения в момент времени
- полная относительная продольная деформация предшествующей ступени нагружения в момент времени  , вычисленная по этой формуле ранее при
, вычисленная по этой формуле ранее при  =0;
=0;
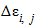 - приращение относительной деформации, определяемое по кривой ползучести (см. 6.3.5.7) и представляющее собой разность между деформацией, накопленной к моменту, когда i-я ступень нагрузки действовала в течение времени
- приращение относительной деформации, определяемое по кривой ползучести (см. 6.3.5.7) и представляющее собой разность между деформацией, накопленной к моменту, когда i-я ступень нагрузки действовала в течение времени  , и деформацией, накопленной к началу действия i-й ступени нагрузки.
, и деформацией, накопленной к началу действия i-й ступени нагрузки.
Моменты времени  назначают одинаковыми для каждой ступени нагружения с учетом требований 6.1.4.3.
назначают одинаковыми для каждой ступени нагружения с учетом требований 6.1.4.3.
Результаты представляют в виде семейства кривых ползучести при постоянных напряжениях 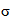 (см. рисунок Ф.1).
(см. рисунок Ф.1).
Ф.4 Для определения параметра 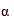 и набора значений
и набора значений 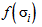 полученные значения представляют в виде семейства параллельных прямых в координатах: In t - ось абсцисс, ln
полученные значения представляют в виде семейства параллельных прямых в координатах: In t - ось абсцисс, ln  - ось ординат (см. рисунок Ф.2). Далее значения
- ось ординат (см. рисунок Ф.2). Далее значения 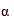 и
и 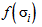 вычисляют по формулам:
вычисляют по формулам:
 ; (Ф.5)
; (Ф.5)
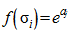 , (Ф.6)
, (Ф.6)
где  и b - параметры, определяемые графически (см. Ф.8) или способом наименьших квадратов.
и b - параметры, определяемые графически (см. Ф.8) или способом наименьших квадратов.
Ф.5 Для модели линейно деформируемого основания набор значений 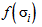 аппроксимируют прямой в координатах:
аппроксимируют прямой в координатах:  - ось абсцисс,
- ось абсцисс, 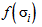 - ось ординат (см. рисунок Ф.3) и вычисляют значение
- ось ординат (см. рисунок Ф.3) и вычисляют значение 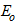 по формуле
по формуле
 , (Ф.7)
, (Ф.7)
где с - параметр, определяемый графически (см. Ф.9) или способом наименьших квадратов.
Ф.6 Для модели нелинейно деформируемого основания набор значений 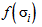 аппроксимируют прямой в координатах In
аппроксимируют прямой в координатах In  - ось абсцисс, In
- ось абсцисс, In 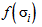 - ось ординат (см. рисунок Ф.4) и вычисляют значения
- ось ординат (см. рисунок Ф.4) и вычисляют значения  и m по формулам:
и m по формулам:
 ; (Ф.8)
; (Ф.8)
 , (Ф.9)
, (Ф.9)
где а и b - параметры, определяемые графически (см. Ф.10) или способом наименьших квадратов.
Ф.7 Коэффициент поперечного расширения  определяют из зависимости, устанавливающей связь между относительными продольными
определяют из зависимости, устанавливающей связь между относительными продольными 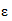 и поперечными
и поперечными 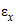 деформациями
деформациями
 . (Ф.10)
. (Ф.10)
Для определения  экспериментальные данные (относительные продольные и поперечные деформации) в конце каждой ступени нагружения представляют в координатах
экспериментальные данные (относительные продольные и поперечные деформации) в конце каждой ступени нагружения представляют в координатах 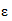 - ось абсцисс,
- ось абсцисс, 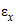 - ось ординат и аппроксимируют прямой, проходящей через начало координат. Значение
- ось ординат и аппроксимируют прямой, проходящей через начало координат. Значение  равно тангенсу угла наклона этой прямой к оси абсцисс.
равно тангенсу угла наклона этой прямой к оси абсцисс.
Ф.8 При графическом способе определения параметров  и b уравнения семейства параллельных прямых (см. рисунок Ф.2) эти параметры равны:
и b уравнения семейства параллельных прямых (см. рисунок Ф.2) эти параметры равны:
 - в масштабе чертежа равен отрезку, отсекаемому на оси ординат j-й из семейства параллельных прямых наилучшего приближения к экспериментальным точкам;
- в масштабе чертежа равен отрезку, отсекаемому на оси ординат j-й из семейства параллельных прямых наилучшего приближения к экспериментальным точкам;
b - в масштабе чертежа равен тангенсу угла наклона семейства параллельных прямых к оси абсцисс.
Ф.9 Параметр с при графическом способе определения в масштабе чертежа равен тангенсу угла наклона к оси абсцисс прямой наилучшего приближения к экспериментальным точкам, проходящей через начало координат (см. рисунок Ф.3).
Ф.10 При графическом способе определения параметров а и b (см. рисунок Ф.4) эти параметры равны:
а - в масштабе чертежа равен отрезку, отсекаемому на оси ординат прямой наилучшего приближения к экспериментальным точкам;
b - в масштабе чертежа равен тангенсу угла наклона этой прямой к оси абсцисс.
Ф.11 Исходные данные и результаты расчета записывают в таблицу Ф.1.




Таблица Ф.1 - Исходные данные и результаты расчета характеристик деформируемости
| Номер ступени нагружения j | Напряжение  , МПа , МПа
| Время отсчета деформаций t, ч | Относительные продольные деформации 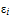
| Приращение относительных продольных деформаций 
| Относительные продольные деформации от постоянных напряжений 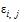
| Относительные поперечные деформации 
| Приращение относительных поперечных деформаций 
| Относительные поперечные деформации от постоянных напряжений 
| Функции напряжений 
|
Окончание таблицы Ф.1
Коэффициент нелинейности во времени 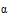
| Модуль линейной деформации 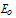 , МПа , МПа
| Коэффициент нелинейной деформации  , , 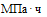
| Модуль предельно длительной деформации E, МПа | Коэффициент предельно длительной нелинейной деформации A, МПа | Коэффициент нелинейности по напряжениям m | Коэффициент поперечного расширения 
| Условно-мгновенное сопротивление  , МПа , МПа
| Предел длительной прочности  , МПа , МПа
| Примечание |
Приложение X
(рекомендуемое)






