Упражнение 1. Определение плотности твердых тел пикнометром
Пикнометр представляет собой стеклянный сосуд определенного объема. Наиболее распространенный тип пикнометра имеет вид колбочки с узким горлышком, на котором нанесена метка. Жидкость наливается до указанной метки. Это контролирует постоянство объема наливаемой жидкости. Из формулы (1) следует, что для вычисления плотности необходимо определить массу и объем исследуемого тела. Массу тела можно определить взвешиванием, а для определения объема тела произвольной формы используют пикнометр.
Пусть общая масса дробинок 
, масса пикнометра, заполненного до метки водой 
. При погружении в пикнометр с водой дробинок, уровень воды поднимается выше метки. Удалим лишнюю воду, доведя ее уровень до метки пикнометра. Массу пикнометра с водой и опущенными дробинками обозначим 
.
Тогда масса вытесненной воды будет равна
Объем пикнометра до метки будет равен
, (1)
где 
- плотность воды.
Поскольку объем вытесненной воды равен объему дробинок, то плотность твердого тела равна
(2)
Последняя формула описывает приближенное значение плотности, так как не учитывает потери веса при взвешивании в воздухе за счет силы Архимеда. С учетом этой поправки плотность определяется формулой
(3)
В этой формуле 
- плотность воздуха.
В данном методе плотность твердого тела вычисляется по формуле, в которую в качестве параметров входят величины 
. Поэтому для вычисления погрешности измерений находим частные производные по каждому из параметров и рассчитываем абсолютные погрешности измерений соответствующих величин:
(4)
(5)
(6)
(7)
Используя закон сложения случайных ошибок, определим суммарную ошибку измерения плотности твердого тела по формуле
. (8)
В результате плотность твердого тела запишется как 
Порядок выполнения работы
1. С помощью весов определите массу пикнометра с водой .
2. С помощью весов определите массу кусочков исследуемого твердого тела (дробинок).
3. Опустите в пикнометр с водой все дробинки. Проследите, чтобы на дробинках не осталось пузырьков воздуха. Избыток воды уберите с помощью пипетки и фильтровальной бумаги. Определите массу пикнометра с водой и дробинками .
4. Из таблицы найдите значение плотности воды, соответствующее температуре воздуха в комнате .
5. Пользуясь формулами (2) и (3), вычислите значение плотности твердого тела.
6. С помощью формул (4) – (7) вычислите погрешность измерения плотности твердого тела.
7. Результаты измерений занесите в таблицу 1.
Таблица 1
| Масса, г |
| |||
|
|
|
|
| |
Упражнение2. Определение плотности твердого тела методом гидростатического взвешивания
Предварительно взвешенный образец покрывают пленкой из парафина. Затем образец охлаждают и взвешивают, сначала на воздухе, затем на гидростатических весах в воде (рис. 4).
Среднюю плотность материала вычисляют по формуле:
, г/см3 (7)
где ρ воды - плотность воды, 1 г/см 3;
ρ пар - плотность парафина, 0,93 г/см;
m - масса образца, г;
m1 - масса парафинированного образца на
воздухе, г;
m2 - масса парафинированного образца
в воде, г;
m1 - m2 - потеря массы в воде, равная
массе вытесненной воды, г
Результаты определения средней плотности материала заносят в табл. 5.
Таблица 5
Определение средней плотности образцов неправильной формы
| Номер опыта | Масса образца, m, г | Масса парафинированного образца на воздухе, m 1, г | Масса парафинированного образца в воде, m 2, г | Средняя плотность, ρ, г/см3 | ||
| полученное значение | среднее значение | по справочным данным | ||||
Приборы и принадлежности: весы с разновесами, сосуд с водой (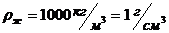
), твердые тела.
Чтобы определить плотность тела, необходимо знать массу тела (ее можно узнать, взвешивая тело на весах) и объем тела (в данной лабораторной работе его определяют методом гидростатического взвешивания). Для того, чтобы понять суть метода гидростатического взвешивания, решим следующую задачу.
Задача. Твердое тело произвольной формы, находящееся в состоянии покоя, взвешивают два раза. Один раз тело взвешивают в воздухе (обычным образом), второй раз – в жидкости (например, в воде), предварительно полностью погрузив в нее тело (см. рис.). Вес тела в воздухе равен 
, в жидкости – 
. Определить объем тела V, если плотность жидкости 
известна.
Дано: 
, 
, .
Найти: 
Решение.
Во втором случае весы показывают вес1) тела  , погруженного в жидкость. При этом на само тело действуют следующие силы:
1.  – сила тяжести, обусловленная гравитационным притяжением со стороны Земли и направленная вниз (здесь – масса тела,  – ускорение свободного падения);
2.  - сила Архимеда (равнодействующая сил давления на тело со стороны жидкости), направленная вверх2);
3.  - сила натяжения нити, направленная вверх и, согласно третьему закону Ньютона, численно равная показанию весов  , т.е.  .
|
|
Если тело покоится, то, согласно первому закону Ньютона, сумма этих сил равна нулю:
или в алгебраическом виде:
.
Откуда 
.
При взвешивании тела в воздухе на него действуют аналогичные силы, но силой Архимеда можно пренебречь ввиду малой плотности воздуха. Поэтому
.
Таким образом, необходимо решить следующую систему уравнений:
,
откуда 
(2)
При использовании рычажных весов с разновесами 
, 
, где 
и 
- массы разновесов при взвешивании тела в воздухе в жидкости. Тогда, объем тела:
(3)
Ответ: объем любого тела, полностью погруженного в жидкость с известной плотностью, можно определить с помощью формул (2) или (3).
Тогда плотность вещества, из которого сделано тонущее тело, можно определить по формуле:
(4)
Полученную плотность следует исправить, учитывая действие выталкивающей силы при взвешивании тела в воздухе. Если при температуре взвешивания плотность воздуха равна 
, (5)
где 
- объем тела, равный объему вытесненной воды. Подставляя выражение для объема в формулу (4), получим
(6)
Поправкой на потерю веса проволоки в воде ввиду ее малости можно пренебречь.
Абсолютную погрешность измерения плотности найдем по формуле
,
где 
Порядок выполнения работы
1. Определите взвешиванием массу исследуемого тела в воздухе.
2. Подвесив тело на тонкой проволоке необходимой длины на крючок чашки весов, определите его массу вместе с проволокой .
3. Установите штатив возле чашки весов, на нем укрепите стакан с
4.
1) Вес тела – это сила, с которой тело действует на опору или подвес. Согласно третьему закону Ньютона, вес тела, приложенный к опоре, по модулю равен силе реакции опоры, действующей на тело, в данном случае – силе натяжения нити.
| 2) Закон Архимеда: | На тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и численно равная весу вытесненной телом жидкости или газа. |
Если система горизонтальна и покоится, то вес вытесненной жидкости численно равен ее силе тяжести (докажите это утверждение). Тогда:
где - плотность жидкости, - объем вытесненной жидкости (в нашем случае он совпадает с объемом тела), - масса вытесненной жидкости (следствие из определения плотности жидкости).
