Раздел1 Теоретическая механика
Номер задачи каждого раздела соответствует четности последней цифры шифра, а исходные данные – последним двум цифрам
Задача 1.1. Определить опорные реакции фермы и силы в стержнях 4,5,6 способом сечений. Данные своего варианта взять из таблицы 1 и схемы на рис.1
Задача 1.2. Определить опорные реакции балок. Данные для задачи взять из таблицы 2 и схемы на рис. 2 согласно своему варианту
Рис.1
| Схема на рисунке 1 | Вариант | F1 | F2 | h1 | h2 | l | Схема на рисунке 1 | Вариант | F1 | F2 | h1 | h2 | l |
| кН | м | кН | м | ||||||||||
| 1 | 00 | 18 | 20 | 4 | - | 4 | V | 05 | 30 | 15 | 1,0 | 2,5 | 2,5 |
| 11 | 20 | 25 | 2,5 | - | 3 | 15 | 25 | 15 | 1,5 | 2,5 | 3,0 | ||
| 21 | 20 | 15 | 3 | - | 2,5 | 25 | 15 | 30 | 1,2 | 2,0 | 3,5 | ||
| 31 | 25 | 18 | 3,5 | - | 2,5 | 35 | 15 | 25 | 0,8 | 2,0 | 4,0 | ||
| 49 | 30 | 30 | 2,5 | - | 2 | 44 | 18 | 30 | 0,5 | 2,5 | 3,0 | ||
| 58 | 15 | 35 | 3 | - | 2 | 54 | 40 | 15 | 1,5 | 2,0 | 3,5 | ||
| 63 | 18 | 25 | 3,5 | - | 3 | 67 | 30 | 25 | 1,2 | 2,5 | 3,0 | ||
| 71 | 40 | 15 | 4 | - | 2,5 | 73 | 15 | 35 | 1,0 | 3,0 | 2,0 | ||
| 81 | 30 | 20 | 3,0 | - | 3,0 | 83 | 25 | 35 | 0,8 | 2,5 | 3,0 | ||
| 91 | 25 | 35 | 3,5 | - | 2,5 | 95 | 20 | 15 | 0,5 | 3,0 | 2,0 | ||
| II | 01 | 15 | 20 | 0,5 | 2 | 2,0 | VI | 04 | 30 | 15 | 1,2 | 2,0 | 2,5 |
| 10 | 20 | 25 | 0,7 | 2 | 2,0 | 14 | 25 | 15 | 1,5 | 2,5 | 3,0 | ||
| 20 | 20 | 15 | 1,0 | 2 | 2,0 | 24 | 15 | 30 | 0,5 | 2,0 | 2,0 | ||
| 30 | 25 | 18 | 1,2 | 2 | 2,5 | 34 | 15 | 25 | 0,8 | 2,5 | 2,0 | ||
| 39 | 30 | 30 | 0,5 | 2,5 | 2,5 | 43 | 18 | 30 | 1,0 | 3,0 | 2,5 | ||
| 59 | 15 | 35 | 0,7 | 2,5 | 3,0 | 55 | 40 | 15 | 1,0 | 2,0 | 4,0 | ||
| 61 | 18 | 25 | 1,0 | 2,5 | 3,5 | 65 | 30 | 25 | 1,2 | 2,5 | 3,5 | ||
| 74 | 40 | 15 | 1,2 | 2,5 | 3,5 | 76 | 15 | 35 | 1,5 | 2,5 | 3,5 | ||
| 84 | 30 | 20 | 0,5 | 3,0 | 3,5 | 86 | 25 | 35 | 0,5 | 3,0 | 2,0 | ||
| 90 | 25 | 35 | 0,7 | 3,0 | 3,0 | 94 | 20 | 15 | 0,8 | 3,0 | 2,5 | ||
| III | 02 | 20 | 20 | 0,5 | 2,5 | 2,5 | VII | 07 | 20 | 4 | 1,2 | 2,5 | 3,0 |
| 12 | 15 | 35 | 0,7 | 2,5 | 2,5 | 17 | 25 | 15 | 1,0 | 2,5 | 2,0 | ||
| 23 | 40 | 15 | 1,0 | 2 | 2,0 | 27 | 15 | 35 | 0,7 | 3,0 | 2,5 | ||
| 33 | 20 | 15 | 1,2 | 2,0 | 2,0 | 37 | 30 | 15 | 0,5 | 3,5 | 3,0 | ||
| 42 | 30 | 25 | 1,5 | 2,5 | 3,0 | 46 | 30 | 20 | 1,5 | 3,0 | 3,5 | ||
| 56 | 18 | 30 | 1,2 | 2,5 | 3,0 | 52 | 20 | 30 | 1,0 | 2,5 | 3,0 | ||
| 62 | 10 | 25 | 1,0 | 2,5 | 2,5 | 66 | 15 | 30 | 1,2 | 2,0 | 2,5 | ||
| 70 | 15 | 30 | 0,7 | 2,0 | 2,5 | 72 | 35 | 15 | 0,5 | 1,5 | 3,0 | ||
| 80 | 25 | 30 | 0,5 | 2,0 | 2,0 | 82 | 15 | 25 | 1,5 | 1,5 | 4,0 | ||
| 93 | 10 | 30 | 1,0 | 2,5 | 2,0 | 97 | 40 | 20 | 1,0 | 2,0 | 2,0 | ||
| IV | 03 | 20 | 20 | 2,0 | - | 2,5 | VIII | 06 | 20 | 40 | 2,5 | - | 3,5 |
| 13 | 15 | 35 | 2,5 | - | 2,0 | 16 | 25 | 15 | 2,0 | - | 2,0 | ||
| 22 | 40 | 15 | 3,0 | - | 3,5 | 26 | 15 | 35 | 3,0 | - | 2,5 | ||
| 32 | 20 | 15 | 4,0 | - | 2,5 | 36 | 30 | 15 | 3,5 | - | 2,0 | ||
| 41 | 30 | 25 | 4,0 | - | 3,5 | 45 | 30 | 20 | 4,0 | - | 3,0 | ||
| 57 | 18 | 30 | 3,5 | - | 2,0 | 53 | 20 | 30 | 4,0 | - | 2,5 | ||
| 60 | 10 | 25 | 3,0 | - | 2,5 | 64 | 15 | 30 | 3,5 | - | 2,0 | ||
| 77 | 15 | 30 | 2,5 | - | 4,5 | 79 | 35 | 15 | 3,0 | - | 2,5 | ||
| 87 | 25 | 30 | 2,0 | - | 3,0 | 89 | 15 | 25 | 2,5 | - | 3,0 | ||
| 92 | 10 | 30 | 4,0 | - | 3,0 | 96 | 40 | 20 | 2,0 | - | 3,5 | ||
| Схема на рисунке 1 | Вариант | F1 | F2 | h1 | h2 | l | Схема на рисунке 1 | Вариант | F1 | F2 | h1 | h2 | l |
| кН | м | кН | м | ||||||||||
| IX | 09 | 20 | 35 | 1,5 | 3,0 | 3,5 | X | 08 | 20 | 35 | 0,5 | 3,0 | 3,5 |
| 19 | 15 | 35 | 1,2 | 2,5 | 3,0 | 18 | 15 | 35 | 0,8 | 2,5 | 3,0 | ||
| 29 | 40 | 15 | 1,0 | 2,0 | 3,0 | 28 | 40 | 15 | 1,0 | 2,5 | 3,5 | ||
| 38 | 20 | 15 | 0,8 | 2,5 | 25 | 40 | 20 | 15 | 1,2 | 3,0 | 3,0 | ||
| 50 | 25 | 30 | 1,5 | 2,0 | 2,5 | 51 | 25 | 30 | 0,5 | 3,0 | 2,5 | ||
| 68 | 15 | 20 | 1,2 | 2,0 | 3,0 | 69 | 15 | 20 | 0,8 | 2,0 | 2,5 | ||
| 75 | 15 | 40 | 1,0 | 2,5 | 3,0 | 78 | 15 | 40 | 1,0 | 3,0 | 3,0 | ||
| 85 | 35 | 15 | 0,8 | 3,0 | 3,5 | 88 | 35 | 15 | 1,2 | 2,5 | 3,5 | ||
| 99 | 35 | 20 | 0,5 | 2,5 | 2,5 | 98 | 35 | 20 | 1,5 | 2,5 | 4,0 | ||
| Рис. 2 |
Таблица 2
| Схема на рис.2 | Вариант | а1 | а2 | а3 | F,кН | gкН/м | М, кН*м | Схема на рис.2 | Вариант | а1 | а2 | а3 | F,кН | gкН/м | М, кН*м |
| м | м | ||||||||||||||
| I | 00 | 0,7 | 0,8 | - | 80 | 15 | 10 | V | 05 | 0,7 | 1,5 | - | 65 | 18 | 25 |
| 11 | 0,5 | 1,0 | - | 120 | 10 | 20 | 15 | 1,0 | 2,0 | - | 40 | 25 | 40 | ||
| 21 | 0,5 | 1,3 | - | 50 | 25 | 30 | 25 | 0,8 | 1,2 | - | 35 | 10 | 20 | ||
| 31 | 0,8 | 1,2 | - | 40 | 30 | 35 | 35 | 0,6 | 1,8 | - | 50 | 8 | 15 | ||
| 49 | 0,6 | 1,0 | - | 60 | 18 | 40 | 44 | 0,5 | 2,3 | - | 80 | 12 | 25 | ||
| 58 | 1,0 | 0,4 | - | 75 | 10 | 25 | 54 | 0,9 | 1,6 | - | 25 | 15 | 35 | ||
| 63 | 0,6 | 0,8 | - | 100 | 12 | 15 | 67 | 0,4 | 2,1 | - | 55 | 20 | 18 | ||
| 71 | 0,5 | 1,0 | - | 125 | 10 | 10 | 73 | 0,8 | 2,2 | - | 40 | 18 | 20 | ||
| 81 | 0,8 | 0,7 | - | 80 | 20 | 25 | 83 | 0,7 | 1,5 | - | 30 | 10 | 15 | ||
| 91 | 0,7 | 1,1 | - | 60 | 15 | 40 | 95 | 0,4 | 1,6 | - | 20 | 12 | 10 | ||
| II | 01 | 1,5 | 0,7 | 0,8 | 15 | 10 | 40 | VI | 04 | 1,5 | 0,7 | 0,8 | 60 | 15 | 35 |
| 10 | 2,0 | 0,5 | 1,0 | 35 | 25 | 18 | 14 | 2,0 | 0,5 | 1,0 | 25 | 8 | 25 | ||
| 20 | 1,2 | 0,5 | 1,3 | 80 | 15 | 20 | 24 | 1,2 | 0,5 | 1,3 | 40 | 10 | 15 | ||
| 30 | 1,0 | 1,2 | 0,8 | 25 | 12 | 15 | 34 | 1,0 | 1,2 | 0,8 | 30 | 20 | 15 | ||
| 39 | 1,4 | 0,6 | 1,0 | 40 | 8 | 20 | 43 | 1,4 | 0,6 | 1,0 | 10 | 25 | 40 | ||
| 59 | 1,6 | 1,0 | 0,4 | 60 | 25 | 10 | 55 | 1,6 | 1,0 | 0,4 | 15 | 20 | 40 | ||
| 61 | 1,8 | 0,8 | 0,6 | 50 | 18 | 25 | 65 | 1,8 | 0,8 | 0,6 | 35 | 18 | 20 | ||
| 74 | 1,5 | 0,5 | 1,0 | 100 | 15 | 18 | 76 | 1,5 | 1,0 | 0,5 | 55 | 12 | 20 | ||
| 84 | 2,0 | 0,8 | 0,7 | 60 | 10 | 25 | 86 | 2,0 | 0,8 | 0,7 | 60 | 10 | 15 | ||
| 90 | 1,2 | 1,1 | 0,7 | 30 | 14 | 10 | 94 | 1,2 | 1,1 | 0,7 | 80 | 15 | 35 | ||
| III | 02 | 1,5 | 0,7 | - | 20 | 15 | 20 | VII | 07 | 0,8 | 1,5 | 0,7 | 35 | 12 | 20 |
| 12 | 0,5 | 2,0 | - | 35 | 10 | 40 | 17 | 1,0 | 2,0 | 0,5 | 80 | 18 | 35 | ||
| 23 | 0,5 | 1,2 | - | 15 | 20 | 35 | 27 | 1,3 | 1,2 | 0,5 | 120 | 15 | 10 | ||
| 33 | 0,8 | 1,0 | - | 40 | 12 | 30 | 37 | 1,2 | 1,0 | 0,8 | 60 | 30 | 25 | ||
| 42 | 0,6 | 1,4 | - | 60 | 20 | 18 | 46 | 1,0 | 1,4 | 0,6 | 50 | 25 | 15 | ||
| 56 | 1,0 | 1,6 | - | 100 | 18 | 20 | 52 | 0,4 | 1,6 | 1,0 | 40 | 10 | 25 | ||
| 62 | 0,6 | 1,8 | - | 35 | 12 | 25 | 66 | 0,8 | 1,8 | 0,6 | 55 | 15 | 40 | ||
| 70 | 0,5 | 1,5 | - | 25 | 10 | 30 | 72 | 1,0 | 1,5 | 0,5 | 70 | 18 | 35 | ||
| 80 | 0,8 | 2,0 | - | 70 | 18 | 15 | 82 | 0,7 | 2,0 | 0,8 | 100 | 12 | 15 | ||
| 93 | 0,7 | 1,2 | - | 120 | 15 | 25 | 97 | 1,1 | 1,2 | 0,7 | 50 | 25 | 10 | ||
| IV | 03 | 0,7 | 1,5 | 0,8 | 25 | 15 | 30 | VIII | 06 | 1,1 | 0,4 | 0,5 | 25 | 15 | 30 |
| 13 | 0,5 | 2,0 | 1,0 | 40 | 10 | 25 | 16 | 0,7 | 1,7 | 0,8 | 40 | 10 | 15 | ||
| 22 | 0,5 | 1,2 | 1,3 | 60 | 18 | 20 | 26 | 1,2 | 1,2 | 0,6 | 60 | 18 | 25 | ||
| 32 | 0,8 | 1,0 | 1,2 | 75 | 10 | 15 | 36 | 0,6 | 1,0 | 1,0 | 80 | 12 | 15 | ||
| 41 | 0,6 | 1,4 | 1,0 | 100 | 12 | 30 | 45 | 0,5 | 1,3 | 1,2 | 100 | 10 | 35 | ||
| 57 | 1,0 | 1,6 | 0,4 | 50 | 25 | 18 | 53 | 0,5 | 0,9 | 1,1 | 120 | 15 | 18 | ||
| 60 | 0,6 | 1,8 | 0,8 | 45 | 20 | 18 | 64 | 1,6 | 1,0 | 0,4 | 80 | 20 | 30 | ||
| 77 | 0,5 | 1,5 | 1,0 | 80 | 10 | 40 | 79 | 1,0 | 1,2 | 0,5 | 60 | 10 | 25 | ||
| 87 | 0,8 | 2,0 | 0,7 | 35 | 15 | 20 | 89 | 0,8 | 0,7 | 0,7 | 50 | 25 | 20 | ||
| 92 | 0,7 | 1,2 | 1,1 | 55 | 20 | 25 | 96 | 0,4 | 1,4 | 0,9 | 40 | 18 | 15 | ||
| 1Х | 09 | 0,8 | 0,7 | 1,5 | 25 | 18 | 40 | Х | 08 | 0,5 | 0,9 | - | 80 | 15 | 25 |
| 19 | 1,0 | 0,5 | 2,0 | 40 | 15 | 25 | 18 | 0,6 | 1,0 | - | 60 | 18 | 15 | ||
| 29 | 1,3 | 0,5 | 1,2 | 55 | 10 | 35 | 28 | 0,4 | 0,8 | - | 120 | 10 | 40 | ||
| 38 | 1,2 | 0,8 | 1,0 | 100 | 12 | 20 | 40 | 0,4 | 0,8 | - | 50 | 14 | 30 | ||
| 48 | 1,0 | 0,6 | 1,4 | 80 | 15 | 40 | 47 | 0,5 | 0,9 | - | 40 | 10 | 25 | ||
| 50 | 0,4 | 1,0 | 1,6 | 60 | 20 | 15 | 51 | 0,6 | 1,0 | - | 30 | 15 | 20 | ||
| 68 | 0,8 | 0,6 | 1,8 | 55 | 25 | 30 | 69 | 0,5 | 0,9 | - | 25 | 18 | 15 | ||
| 75 | 1,0 | 0,5 | 1,5 | 35 | 18 | 15 | 78 | 0,6 | 0,9 | - | 55 | 20 | 25 | ||
| 85 | 0,7 | 0,8 | 2,0 | 25 | 20 | 35 | 88 | 0,6 | 0,9 | - | 60 | 18 | 40 | ||
| 99 | 1,1 | 0,7 | 1,2 | 50 | 15 | 30 | 98 | 0,6 | 1,0 | - | 80 | 14 | 30 | ||
Указания к решению задач 1.1
К решению этой задачи можно приступать после проработки тем «Пара сил» и «Плоская система произвольно расположенных сил».
В задаче 1 требуется определить опорные реакции фермы и силы в стержнях 4, 5, 6 способом сквозного сечения. Ферма имеет две опоры (см. рис. 1). Опора А — шарнирно-подвижная, препятствует лишь поступательному перемещению тела по нормали к опорной плоскости и, следовательно, накладывает на него одну связь. Реакция такой опоры перпендикулярна опорной плоскости (рис.3а),
Опора В —шарнирно-неподвижная (рис.3 б) накладывает на тело две связи и препятствует поступательным перемещениям вдоль обеих координатных осей. Опорная реакция содержит составляющие.
Для решения задачи необходимо мысленно освободиться от опор, заменив их действие на ферму реакциями (рис.4). Принято обозначать реакции
Рис. 3 Рис. 4
направленные по горизонтали — Н направленные вертикально — V. Вместо опоры А прикладываем реакцию НА вместо опоры В прикладываем горизонтальную НВ и вертикальную Vb составляющие реакции. В результате получаем систему произвольно расположенных сил: F 1, F 2, На, НВ, Vb.
Необходимо твердо усвоить условия равновесия плоской системы произвольно расположенных сил и уметь составлять для такой системы уравнения равновесия в трех формах:
Σ Үi = 0 или Σ Xi = 0; Σ MA = 0; Σ МB = 0;
Σ Хi = 0; Σ Үi = 0; Σ Мо = 0;
Σ MA = 0; Σ МB = 0; Σ Мо = 0;
а для плоской системы параллельных сил — в двух формах:
Σ MA = 0; Σ МB = 0;
Σ Үi = 0; Σ Мо = 0.
Для нашей задачи наиболее удобна система уравнений
Σ Үi = 0 Σ MA = 0; Σ МB = 0.
Составим эти уравнения, расположив ось у вдоль стержня 7:
Σ Үi = Vb - F 2, - F 1 = 0
При составлении уравнений моментов необходимо помнить, что моментом силы относительно точки называется произведение модуля этой силы на плечо, т. е. на кратчайшее расстояние от точки до линии действия силы. Момент силы; считаетсяположительным если сила производит вращение по ходу: часовой стрелки и отрицательным, если — против часовой стрелки. Если линия действия седы, проходит через точку, относительно которой силы равен нулю:
Σ MA= F2, а 1 + F1l – HBh1=0
Σ MB= HAh1 + F2a1+– F1 l=0
Из первого уравнения находим
VB = F2 +F1 = 10+10 = 20 кН.
Из второго
Из третьего
Реакции НА и Нв численно равны и противоположны по направлению, что удовлетворяет уравнению ΣХi = НА+ НВ= -24+24=0. В качестве проверки найденных реакций можно составить уравнение относительно какой-либо другой точки, например Е:
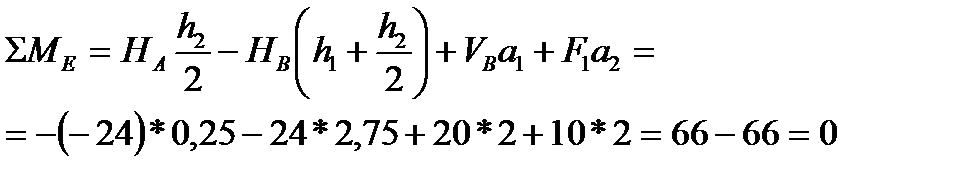
Реакции определены правильно — их значения удовлетворяют уравняю.
Для определения сил в стержнях 4,5,6 проведем сквозное сечение /—/ (рис.4), разделяющее ферму на две части. Отбросим мысленно правую часть фермы, а левую изобразим; отдельно (рис.5). Эта часть фермы находится в равновесии под действием, произвольной плоской системы шести сил: трех известных НА, НВ, VВ и трех искомых реакций R4 R5 R6. Для определения реакций R4 R5 R6 воспользуемся тремя уравнениями моментов, выбрав моментные точки так, чтобы в каждое из трех уравнений вошла одна
неизвестная сила. Такими точками являются пересечения двух стержней, так как моменты сил, линии действия которых проходят через такую точку, равняются нулю. Для данной системы сил (рис.5 а) в качестве моментных точек целесообразно выбрать:
точку В — в ней пересекаются линии сил R 5 R 4; можно определить силу R 6
точку Е — в ней пересекаются линий сил R 5 и R 6; можно определить силу. R 4 (рис.5б);
точку С, в которой пересекаются линии сил R 6 и R 4 можно определить силу R 5 (рис 5 в).
Составим уравнение моментов всех сил, приложенных к рассматриваемой части фермы относительно точки В. Для удобства разложим силу R 6 на составляющие: горизонтальную R 6 cos 7° и вертикальную R 6 cos 83 ° и возьмем момент каждой из них в отдельности.
Так как линия действия вертикальной составляющей проходит через точку В, ее момент равен нулю и в уравнение войдет момент только от горизонтальной составляющей реакции (рис. 5 а).
Σ М B = - НА h1 + R6 cos 7°* h1. =0;
| Рис.5 |
Отсюда R6=24,2 кН.
Определяем R 4, составляющие которой R 4 с os 37° — горизонтальная и R 4, cos 53° — вертикальная (рис. 3, б). Составляющие искомой реакции не обязательно показывать на рисунке, достаточно их мысленно представить и не забывать включать в уравнение.
Σ МЕ = НА.*0,5h2 - HB(h1 +0,5 h2) +VBa1+R4 cos 53° a1 -R4 cos37° (h1+0,5h2) =0.
24*0,25-24*2,5 + 20*2 +2R4*0,60 -2,75R4 *0,80 = 0.
Отсюда R4= -20 кН.
Для определения силы R 5 составляем уравнение моментов всех сил относительно точки С (рис. 5 в).
Горизонтальная составляющая R 5 cos 54°.
Вертикальная составляющая R 5 cos 36°.
Σ MC = НА h2 - HB (h1 + h2 + R5 cos 36°* l R5 cos 54° (h1 +h2) + VBl = 0
24*0,5-24-3,0 + R5* 0,81 *4,0 - R5*0,59*3,0 + 20*4,0 = 0.
Отсюда R 5 = - 13,5 кН.
Чтобы убедиться в правильности вычисленных реакций, спроецируем все силы на ось х (илиось у);
Σ Х i = - НА + Н B + R6 cos 7° + R5cos 54° + R4 cos 37° =
= -24+ 24+ 24,2*0,99 -13,5*0,588 – 20*0,809 =
=-24 + 24 + 24 - 8,10 - 16 ≈ 0.
Следовательно, реакции определены верно. Можно было отбросить левую часть фермы относительно сечения 1-1 и рассмотреть равновесие оставшейся правой части аналогичным образом. Учащимся предоставляется право самостоятельного выбора.
В итоге: стержень 4 сжат силой N 4 = R 4 = 20 кН, стержень 5 сжат силой N 5 = R 5 = 13,5 кН, стержень 6 растянут силой N 6 = R 6 = 24,2 кН.
В задаче 1.2 требуется определить значения опорных реакции балок двухопорной или жестко защемленной.
а) Двухопорная балка (рис.6 а).Обозначим шарнирно-неподвижную опору А, шарнирно-подвижную В. В предыдущей задач мы встречались с такого рода опорами. Изобразим расчетную схем, балки (рис.6 б ) Освобождаем балку от связей, заменяя их действие на балку опорными вертикальными реакциями Va. и Vb, поскольку в данной задаче, кроме сосредоточенного момента, внешние нагрузки только вертикальные. Для удобства расчета равномерно распределенную нагрузку заменяем равнодействующей Fq которая равна произведению интенсивности.q (кН/м) на длину участка ее приложения, т.е. Fq = ql = 10-3 = 30 кН. Линия действия равнодействующей проходит через середину участка, занятого равномерно распределенной нагрузкой.
На расчетной схеме балки (рис. 6 б) должны быть проставлены расстояния от сил до каждой из опор. Особое внимание обратит на расположение распределенной нагрузки на балках с консолями, чтобы избежать ошибок, часто возникающих при определении плеч силы Fq. Значение сосредоточенного момента в любое уравнении равновесия входит с тем знаком, который ему приписывается с учетом направления действия.
Для двухопорных балочных систем при определении опорных реакций самыми рациональными являются уравнения моментов относительно опор А и В. Составляем эти уравнения:
Σ MA= Fqb+M-VB(b+c)+F(b+c+d)=0
Σ MB=VA(b+c)-Fqc+M+Fd=0
Так как определение реакций - первый этап расчета балки на изгиб, то его следует считать особенно ответственным. Поэтому во избежание ошибок при вычислении необходимо производить проверку найденных значений реакций. Составим уравнение проекций всех сил на ось у.
Σ Yi = VA - Fq + VB - F = 13.3-30+31.7-15=45-45=0
Если это равенство не удовлетворяется, следовательно, при определении опорных реакций была допущена ошибка.
Рис.6 Рис.7
б) Консольная балка (рис. 7а) балка с защемленной опорой называется консолью. Защемляющая неподвижная опора лишает балку всех трех степеней свободы: линейных перемещений вдоль осей х и у и возможности поворота в плоскости этих осей. Соответственно в защемлении появляются три неизвестные реакции: VA, HA и реактивный момент заделки МА (рис 7 б). Для их определения наиболее удобными являются следующие условия равновесия:
1. Уравнение моментов сил относительно точки заделки МА=0 – для определения реактивного момента МА, так как силы VA и НА, приложенные к точке А, в уравнение не войдут (их моменты относительно точки А равны нулю)
2. ΣYi =0 –для определения вертикальной реакцииVA
3. ΣХi =0 – для определения горизонтальной реакции НА.
По расчетной схеме балки (рис 7б) составим уравнения равновесия
МА= - МА+ Fa +M+ Fq(b+a)=0
Отсюда
МА= Fa+М+ Fq(b+a)=8*0,5+10+2*1,5=17 кН*м
Значение МА ≥0; следовательно, принятое направление момента правильное.
Из уравнения ΣYi=VA-F-Fq=0 находим VA= F+Fq=8+2=10 к Н
Из уравнения ΣХi =0 следует, что НА=0
Для проверки решения удобно составить уравнение момента относительно произвольно взятой точки, например В:
ΣМВ=-МА+М+VAl-F(b+c) – Fqc= -17+10+10*2.5-8*1.5-2*0.5=-30+30=0
Раздел II Сопротивление материалов
Задача 2.1 Для ступенчатого стального бруса требуется: а) определить значение продольной силы и нормального напряжения по длине бруса; б) построить эпюры N и σ; в) определить абсолютное удлинение (укорочение) бруса. Модуль продольной упругости Е=2*105МПа. Данные для задачи своего варианта взять из табл.3 и схемы на рис.9
Задача 2.2 Построить эпюры изгибающих моментов МХ и поперечных сил Qх для балок задачи раздела «Теоретическая механика»
Исходные данные к 2-1
Рис.8
| Схема | Вариант
| F1 | F2 | A1 | A2 | A3 | a1 | a2 | a3 | a4 |
| кН | см2 | см | ||||||||
| 1 | 00 | 120 | 70 | 16 | 12 | 8 | 60 | 40 | 80 | 70 |
| 11 | 150 | 120 | 25 | 15 | 10 | 80 | 20 | 60 | 50 | |
| 21 | 200 | 150 | 20 | 16 | 10 | 70 | 50 | 100 | 800 | |
| 31 | 140 | 100 | 22 | 20 | 15 | 40 | 60 | 70 | 80 | |
| 49 | 220 | 100 | 20 | 18 | 12 | 50 | 70 | 80 | 100 | |
| 58 | 130 | 120 | 20 | 18 | 15 | 80 | 40 | 50 | 60 | |
| 63 | 180 | 50 | 18 | 15 | 8 | 90 | 30 | 50 | 40 | |
| 71 | 150 | 100 | 18 | 12 | 10 | 70 | 80 | 80 | 90 | |
| 81 | 250 | 60 | 25 | 20 | 15 | 50 | 60 | 70 | 40 | |
| 91 | 110 | 90 | 20 | 15 | 10 | 40 | 30 | 70 | 50 | |
| 2 | 01 | 130 | 120 | 12 | 16 | 8 | 80 | 40 | 50 | 60 |
| 10 | 150 | 120 | 15 | 25 | 10 | 60 | 20 | 40 | 80 | |
| 20 | 120 | 70 | 16 | 20 | 10 | 100 | 50 | 30 | 70 | |
| 30 | 220 | 100 | 20 | 22 | 15 | 70 | 60 | 20 | 50 | |
| 39 | 150 | 100 | 18 | 20 | 12 | 80 | 70 | 20 | 50 | |
| 59 | 250 | 50 | 18 | 20 | 15 | 50 | 40 | 60 | 80 | |
| 61 | 110 | 90 | 15 | 18 | 8 | 50 | 30 | 40 | 90 | |
| 74 | 140 | 100 | 12 | 18 | 10 | 80 | 80 | 30 | 70 | |
| 84 | 200 | 150 | 20 | 25 | 15 | 70 | 60 | 20 | 50 | |
| 90 | 180 | 150 | 15 | 20 | 10 | 90 | 30 | 50 | 70 | |
| Схема | Вариант
| F1 | F2 | A1 | A2 | A3 | a1 | a2 | a3 | a4 |
| кН | см2 | см | ||||||||
| 3 | 02 | 70 | 120 | 16 | 8 | 12 | 10 | 40 | 70 | 80 |
| 12 | 120 | 150 | 25 | 10 | 15 | 20 | 30 | 50 | 60 | |
| 23 | 150 | 200 | 20 | 10 | 16 | 15 | 50 | 80 | 100 | |
| 33 | 100 | 140 | 22 | 15 | 20 | 10 | 60 | 80 | 70 | |
| 42 | 100 | 220 | 20 | 12 | 18 | 15 | 70 | 100 | 80 | |
| 56 | 120 | 180 | 20 | 15 | 18 | 20 | 40 | 60 | 50 | |
| 62 | 50 | 180 | 18 | 8 | 15 | 10 | 30 | 40 | 50 | |
| 70 | 100 | 150 | 18 | 10 | 12 | 20 | 50 | 90 | 80 | |
| 80 | 50 | 250 | 25 | 15 | 20 | 15 | 30 | 40 | 70 | |
| 93 | 90 | 110 | 20 | 10 | 15 | 15 | 40 | 70 | 70 | |
| 4 | 03 | 10 | 70 | 5 | 8 | 12 | 70 | 80 | 10 | 40 |
| 13 | 20 | 120 | 8 | 10 | 15 | 50 | 60 | 20 | 30 | |
| 22 | 25 | 150 | 12 | 15 | 20 | 80 | 100 | 15 | 50 | |
| 32 | 30 | 100 | 16 | 20 | 25 | 80 | 70 | 10 | 60 | |
| 41 | 40 | 100 | 15 | 18 | 25 | 100 | 80 | 15 | 70 | |
| 57 | 45 | 120 | 18 | 25 | 30 | 60 | 50 | 20 | 40 | |
| 60 | 40 | 140 | 16 | 20 | 25 | 40 | 50 | 10 | 60 | |
| 77 | 35 | 75 | 14 | 18 | 20 | 90 | 80 | 20 | 50 | |
| 87 | 25 | 125 | 12 | 165 | 20 | 40 | 70 | 15 | 80 | |
| 92 | 20 | 80 | 10 | 15 | 18 | 50 | 70 | 15 | 60 | |
| 5 | 05 | 70 | 120 | 16 | 8 | 12 | 60 | 10 | 40 | 100 |
| 15 | 120 | 250 | 25 | 10 | 15 | 80 | 20 | 30 | 90 | |
| 25 | 150 | 200 | 22 | 15 | 20 | 70 | 15 | 50 | 80 | |
| 35 | 100 | 140 | 30 | 20 | 25 | 40 | 10 | 60 | 70 | |
| 44 | 100 | 220 | 30 | 18 | 25 | 50 | 15 | 70 | 120 | |
| 54 | 120 | 180 | 35 | 25 | 30 | 80 | 20 | 40 | 100 | |
| 67 | 50 | 180 | 30 | 20 | 25 | 50 | 10 | 30 | 90 | |
| 73 | 70 | 150 | 25 | 18 | 20 | 70 | 20 | 50 | 150 | |
| 83 | 50 | 250 | 25 | 16 | 20 | 60 | 15 | 30 | 100 | |
| 95 | 90 | 190 | 25 | 15 | 18 | 70 | 15 | 40 | 90 | |
| 6 | 04 | 70 | 120 | 16 | 8 | 12 | 80 | 60 | 40 | 50 |
| 14 | 120 | 150 | 25 | 10 | 15 | 60 | 80 | 20 | 40 | |
| 24 | 150 | 200 | 22 | 15 | 20 | 100 | 70 | 50 | 30 | |
| 34 | 100 | 140 | 30 | 20 | 25 | 70 | 40 | 60 | 20 | |
| 43 | 100 | 220 | 30 | 18 | 25 | 80 | 50 | 30 | 30 | |
| 55 | 120 | 180 | 35 | 25 | 30 | 50 | 80 | 40 | 70 | |
| 65 | 50 | 180 | 30 | 20 | 25 | 50 | 90 | 30 | 20 | |
| 76 | 70 | 150 | 25 | 18 | 20 | 80 | 70 | 30 | 50 | |
| 86 | 50 | 250 | 25 | 16 | 20 | 70 | 50 | 20 | 40 | |
| 94 | 90 | 110 | 25 | 15 | 18 | 90 | 70 | 30 | 60 | |
| Схема | Вариант
| F1 | F2 | A1 | A2 | A3 | a1 | a2 | a3 | a4 |
| кН | см2 | см | ||||||||
| 7 | 07 | 120 | 70 | 8 | 16 | 12 | 100 | 40 | 50 | 60 |
| 17 | 150 | 120 | 10 | 22 | 15 | 90 | 20 | 40 | 80 | |
| 27 | 200 | 150 | 15 | 25 | 20 | 80 | 50 | 30 | 70 | |
| 37 | 140 | 100 | 12 | 30 | 25 | 70 | 60 | 20 | 40 | |
| 46 | 220 | 100 | 8 | 20 | 15 | 120 | 30 | 20 | 50 | |
| 52 | 130 | 120 | 15 | 30 | 20 | 100 | 40 | 40 | 80 | |
| 66 | 180 | 50 | 12 | 35 | 25 | 90 | 30 | 40 | 90 | |
| 72 | 150 | 100 | 8 | 25 | 20 | 150 | 30 | 70 | 70 | |
| 82 | 250 | 50 | 10 | 30 | 25 | 100 | 20 | 60 | 50 | |
| 97 | 110 | 90 | 15 | 25 | 18 | 90 | 30 | 50 | 70 | |
| 8 | 06 | 120 | 130 | 16 | 12 | 8 | 60 | 80 | 40 | 40 |
| 16 | 150 | 120 | 22 | 15 | 8 | 50 | 60 | 30 | 30 | |
| 26 | 70 | 120 | 25 | 20 | 12 | 80 | 100 | 50 | 50 | |
| 36 | 100 | 220 | 30 | 25 | 16 | 60 | 70 | 60 | 60 | |
| 45 | 100 | 150 | 20 | 15 | 10 | 50 | 80 | 70 | 70 | |
| 53 | 50 | 250 | 30 | 20 | 16 | 30 | 50 | 40 | 40 | |
| 64 | 90 | 110 | 35 | 25 | 15 | 40 | 50 | 30 | 30 | |
| 79 | 100 | 140 | 25 | 20 | 12 | 60 | 80 | 50 | 50 | |
| 89 | 150 | 200 | 30 | 25 | 12 | 50 | 70 | 30 | 30 | |
| 96 | 150 | 80 | 25 | 18 | 10 | 70 | 90 | 40 | 40 | |
| 9 | 09 | 90 | 240 | 16 | 12 | 10 | 10 | 60 | 80 | 70 |
| 19 | 120 | 220 | 22 | 15 | 12 | 20 | 80 | 60 | 50 | |
| 29 | 50 | 180 | 25 | 20 | 15 | 15 | 70 | 100 | 80 | |
| 38 | 100 | 150 | 30 | 25 | 16 | 10 | 40 | 70 | 80 | |
| 48 | 50 | 250 | 20 | 15 | 10 | 15 | 50 | 80 | 100 | |
| 50 | 70 | 170 | 30 | 20 | 12 | 20 | 80 | 50 | 60 | |
| 68 | 100 | 180 | 35 | 25 | 12 | 10 | 50 | 50 | 40 | |
| 75 | 140 | 220 | 25 | 20 | 10 | 20 | 70 | 80 | 90 | |
| 85 | 130 | 180 | 30 | 25 | 14 | 15 | 60 | 70 | 40 | |
| 99 | 80 | 150 | 20 | 18 | 10 | 15 | 70 | 90 | 70 | |
| 10 | 08 | 100 | 230 | 8 | 12 | 10 | 80 | 50 | 40 | 50 |
| 18 | 110 | 210 | 10 | 14 | 12 | 60 | 40 | 20 | 40 | |
| 28 | 60 | 180 | 12 | 16 | 14 | 100 | 30 | 50 | 30 | |
| 40 | 90 | 140 | 14 | 18 | 16 | 70 | 20 | 60 | 20 | |
| 47 | 60 | 160 | 8 | 12 | 10 | 80 | 20 | 30 | 20 | |
| 51 | 120 | 200 | 10 | 14 | 12 | 70 | 40 | 40 | 60 | |
| 69 | 140 | 220 | 12 | 16 | 14 | 60 | 40 | 30 | 40 | |
| 78 | 100 | 180 | 14 | 18 | 16 | 80 | 30 | 30 | 30 | |
| 88 | 120 | 170 | 8 | 12 | 10 | 70 | 50 | 20 | 20 | |
| 98 | 80 | 150 | 10 | 14 | 12 | 100 | 40 | 30 | 50 | |
Указания к решению задач
Задача 2.1
Прежде чем приступить к решению задачи 1, следует изучит тему 2.2. Цель задачи: а) научить определять продольную силу и нормальные напряжения в сечении ступенчатого бруса (стержня) при действии на него нескольких внешних сил; б) научить строить эпюры N и σ, т. е. графики изменения продольной силы N и нормального напряжения σ, по длине бруса.
Условие задачи. По оси стального ступенчатого стержня (рис9 а) приложены силы F1и F2, значения которых, а также площади поперечных сечений и длины участков указаны на рисунке. Построить эпюры продольных сил и нормальных напряжений и определить полное удлинение стержня. Модуль продольной упругости материала стержня Е = 2-105 МН/м2.
Решение. Верхний конец стержня (рис. 9) жестко заделан. Нижний конец свободен. Прежде чем приступить к определению внутренних сил, разбиваем стержень, на отдельные участки начиная со свободногоконца. Границами участков являются сечения, в которых приложены внешние силы или в которых изменяются размеры поперечного сечения стержня. Рассмотрим брус по высоте.
Рис.9
Первый участок АВ от точки приложения силы F 1 т. е от нижнего торца бруса до сечения, в котором происходит изменение его размеров. Второй
участок ВС до сечения, в котором приложена сила F 2. Третий уча
сток CD от места приложения силы F 2 до заделки.
Пользуясь методом сечений, определяем значения внутренних продольных сил в сечениях стержня. Поскольку нижний конец не закреплен, удобнее начинать именно с него, не определяя реакций заделки стержня.
Проводим сечение 1—1 в пределах первого участка. Необходимо представить сечение 1—1 как бы скользящим, что позволяет просматривать участок по высоте стержня.
Мысленно отбросим верхнюю часть до сечения 1—1 (рис. 9б) и, рассматривая оставшуюся нижнюю часть в состоянии равновесия, составим уравнение проекций сил на ось у: N 1 — F 1 = 0, откуда N 1 = F 1 = 150кН=0,15МН.
Продольная сила положительна, следовательно, на участке АВ имеет место растяжение.
Проводим сечение II — II на участке ВС стержня и отбросим верхнюю часть (рис. 9,в). По аналогии с предыдущим записываем уравнение равновесия N 2 —F1 = 0 и находим из него N 2 =150 кН= 0,15 МН. Участок ВС также растянут.
Проводим сечение III - III на участке CD и отбрасывая верхнюю часть стержня (рис. 9, г), запишем уравнение равновесия нижней части: N 3 + F 2 - F 12 =0, отсюда N 3 = F 1 — F 2 =150- 200=-50 кН = -0,05 МН.
Продольная сила отрицательна, а следовательно, третий участок стержня сжат.
Зная продольную силу на каждом из трех участков, определим значения нормальных напряжений, имея в виду, что А1 =18 см 2=0,0018 м2; А2 = 12 см2-0,0012 м2:
По найденным значениям N и а строим их эпюры, (рис.9 е). Для этого проводим две прямые (базовые линии), параллельные оси стержня. Каждой точке этой прямой соответствует определенное сечение стержня. Считая прямые за нулевые линии, откладываем вправо и влево от них соответственно положительные и отрицательные значения N и σ. Знаки на эпюрах ставятся обязательно. Подписываем значения отложенных ординат. Эпюры штрихуются линиями, перпендикулярными нулевой линии. Длина каждого штриха выражает значение той или другой величины в соответствующем сечении стержня бруса.
Определяем полное удлинение стержня
Подсчитав числовое значение, получим
Задача 2.2
Условие задачи. Построить эпюры внутренних силовых факторов (Мх и Qx) для балок, изображенных на рисунке 10 а, 11 а.
Схемы балок взяты из примера к задаче 1.2 первого раздела (см. рис 6 и 7), где были определены опорные реакции и выполнена проверка правильности их определения (первая стадия расчета балочных систем). На втором этапе выполняется построение эпюр изгибающих моментов Мх и поперечных сил Q х. Основываясь на расчете, выполненном в предыдущей контрольной работе, решение данной задачи следует начинать сразу со второго этапа.
Решение. Сначала построим эпюру Q х
Из теоретического курса известно» что на участке балки с равномерно распределенной нагрузкой эпюра Qx ограничивается наклонной прямой, а на участке, на котором нет распределенной нагрузки, — прямой, параллельной оси, поэтому для построения эпюры поперечных сил достаточно определить значения Qx в начале и конце каждого участка. В сечении, соответствующем точке приложения сосредоточенной силы, поперечная сила должна быть вычислена чуть левее этой точки (на бесконечно близком расстоянии от нее) и чуть правее ее; поперечные силы в таких местах обозначаются соответственно 
и 
Рис.10
Строим эпюру Qx методом характерных точек, ходом слева: а) Для двухопорной балки такими точками будут С и D —начало.и конец распределенной нагрузки, а также А и В — точки приложения опорных реакций, Е — точка приложения сосредоточенн
