1. Определить внешний скручивающий момент М, Н×м, по формуле
М = 
,
где Р – мощность, Вт;
w- угловая скорость, с -1.
2. Определить уравновешивающий момент, используя уравнение равновесия Σ М кz = 0, так как при равномерном вращении вала алгебраическая сумма приложенных к нему внешних скручивающих (вращающих) моментов равна нулю.
3. Пользуясь методом сечений, построить эпюру крутящих моментов по длине вала.
4. Для участка вала, в котором возникает наибольший крутящий момент, определить диаметр вала круглого или кольцевого сечения:
а) из условия прочности
Сечение вала - круг: 
;
Сечение вала - кольцо: 
,
б) из условия жесткости
Сечение вала - круг: 
;
Сечение вала - кольцо: 
Из двух полученных диаметров вала выбрать наибольший.
Пример решения задания 5
Для стального вала круглого поперечного сечения постоянного по длине, показанного на рисунке 12, требуется:
1) определить значения моментов М2, М3, соответствующие передаваемым мощностям Р 2 , Р 3, а также уравновешивающий момент М 1;
2) построить эпюру крутящих моментов;
3) определить требуемый диаметр вала из расчетов на прочность и жесткость, если:
[tк] = 30 МПа; [φ 0] = 0,02 рад/м; w = 20 с -1; Р 2 =52 кВт; Р 3 =50 кВт;
G = 8 × 104 МПа.
Окончательное значение диаметра округлить до ближайшего четного (или оканчивающего на пять) числа.
Решение
1 Определяем величины скручивающих моментов М 2 и М 3
;
.
2 Определяем уравновешивающий момент М 1
SМz = 0; - М 1 + М 2 + М 3 =0;
М 1 = М 2 + М 3; М 1 = 2600 + 2500 = 5100 Н ×м;
3 Строим эпюру М z в соответствии с рисунком 14.
Рисунок 12
4 Определяем диаметр вала для опасного участка, из условий прочности и жесткости (М z maх = 5100 Н ×м).
Из условия прочности:
.
Из условия жесткости:
= 75,5 мм
Ответ: Требуемый диаметр вала получился больше из расчета на прочность, поэтому его принимаем как окончательный: d = 96 мм.
Задание 6 по теме «Изгиб»
Рекомендуемая последовательностьрешения задания 6
1. Определить опорные реакции.
2. Балку разделить на участки по характерным сечениям.
3. Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюры поперечных сил.
4. Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки, вычислить изгибающие моменты в характерных сечениях и построить эпюры изгибающих моментов.
5. Для данной балки, имеющей по всей длине постоянное поперечное сечение, выполнить проектный расчет, т.е. определить Wx в опасном сече-нии, где изгибающий момент имеет наибольшее по модулю значение.
Пример решения задания 6
Для заданной консольной балки (рисунок 13) построить эпюры Q y, M x и подобрать двутавровое сечение, если:
[s] = 160 МПа, F 1 = 2 кН, F 2 = 1 кН, М = 12 кН×м.
Решение
1. Делим балку на участки по характерным сечениям А, В, С
2. Определяем значения поперечной силы Q y и строим эпюру.
1 участок: QУ1 = - F2; QУ1 = - 1 кН;
2 участок: QУ2 = - F2 + F1; QУ2 = - 1 + 2 = 1 кН.
3. Определяем значения изгибающих моментов Мх в характерных сечениях и строим эпюру Мх (рисунок 15).
Рисунок 13
1 участок:
М х 1 = 
,
при z 1 = 0; М х А = 0;
при z 1 = 3 м; М х В =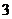 
кН×м.
2 участок:
М х 2 =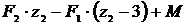 
;
при z 2 = 3 м; М х В = 15 кН×м;
при z 2 = 5 м; М х С = 13 кН×м.
4. Исходя из эпюры изгибающих моментов, определим М х maх
М х maх = 15 кН×м = 
5. Вычисляем осевой момент сопротивления сечения, исходя из условия прочности:
Wx ³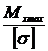 
; Wx = 
;
В соответствии с ГОСТ 8239-72 выбираем двутавр №16,W x mаб=109см 3.
Ответ: в соответствии с ГОСТ 8239-72 выбираем двутавр №16, W x mаб=109см 3.
