Смешанное соединение резисторов представляет собой комбинацию последовательного и параллельного соединений. На рис.18а показан пример смешанного соединения. В этой схеме резисторы R2 и R3 соединены параллельно. Последовательно с этими резисторами подключён резистор R1.
При решении задач на смешанное соединение требуется прежде всего, провести анализ схемы. Необходимо нарисовать схему, обозначить все её элементы, а также токи и напряжения, действующие в схеме. Следует мысленно выделить на схеме элементы соединенные параллельно или последовательно и затем, поэтапно, упростить схему.
На рис.18а показана исходная схема, а затем этапы её упрощения на рис.18б и 18в. Заметьте, что номера токов и напряжений, обозначенных на схеме, всегда совпадают с номером соответствующего сопротивления.
Прежде всего, проведено объединение параллельно соединённых резисторов R2 и R3 в одно сопротивление R2,3. В результате, схема приобрела вид, показанный на рис.18б. На этой схеме видно, что сопротивления R1 и R2,3 соединены последовательно.
Объединяя сопротивления R1 и R2,3, получим общее сопротивление, что показано на рис.18в.
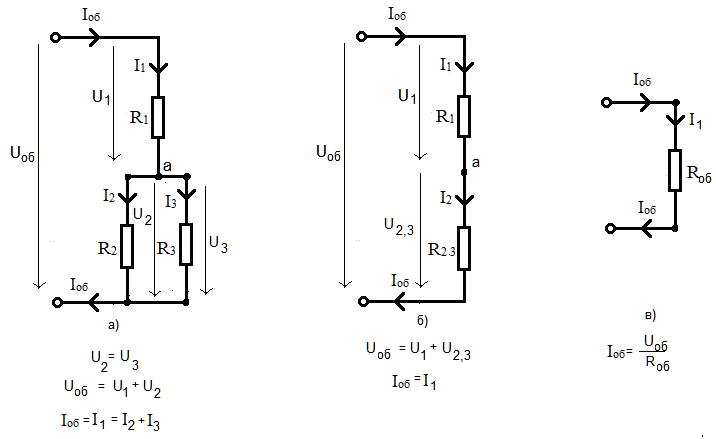
Рис. 18. Смешанное соединение резисторов: а) исходная схема; б) и в) схемы после упрощения
Далее нужно проанализировать схему, рассмотреть, как в ней протекает ток. На схеме, показанной на рис.18а общий для всей схемы ток Iоб, протекая от верхней клеммы, через резистор R1, где он же обозначен как I1, доходит до узла а (см. рис. 18а).
В узле а ток разделяется на две ветви. По первому закону Кирхгофа I1 равен сумме токов I2+I3. Далее эти токи вновь сливаются в общий ток Iоб, который идёт к нижней клемме. Напряжения на параллельно соединённых резисторах R2 и R3 одинаковы.
В схеме на рис. 18б всё уже проще. Видно, что резисторы R1 и R2,3 соединены последовательно. Через всю цепь ток, одинаковый во обоих сопротивлениях. Общее напряжение, приложенное к цепи, равно сумме напряжений на резисторах R1 и R2,3.
Совсем просто выглядит схема на рис. 18в. В этой схеме только одно сопротивление.
После упрощения схемы следует записать под каждой из них соотношения для токов и напряжений, используя свойства последовательного и параллельного соединения. Такая запись показана на рис.18. Начинать запись соотношений следует с самой простой схемы, т.е. с рис.18в.
После проведения анализа схемы и её упрощения можно приступать к решению задачи на смешанное соединение? Руководствуясь записанными выше соотношениями для каждой схемы.
Пример 9. Расчёт цепи со смешанным соединением резисторов
Для схемы, показанной на рис.18 известно общее напряжение, равное 120В
Известна величина каждого сопротивления: R1=16Ом, R2=40Ом и R3=60Ом. Найти: общее сопротивление схемы, все токи и напряжения, обозначенные на схеме.
Решение:
1. Найдём общее сопротивление цепи:
1.1. Общее сопротивление резисторов R2 и R3:
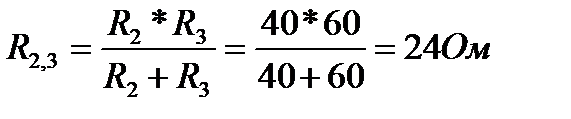
1.2. Общее сопротивление всей цепи:
Rоб= R1+R2,3=16+24=40Ом
2. Находим общий ток, потребляемый схемой:
Iоб=Uоб/ Rоб=120/40=3А= I1
3. Определяем напряжение на резисторе R1:
U1= I1• R1=3*16=48В
4. Найдём напряжение на параллельно включённых резисторах R2 и R3:
U2,3= Uоб - U1 = 120 - 48 =72В = U2= U3
5. Найдем токи в резисторах R2 и R3:
I2= U2/ R2= 72/40 = 1,8А
I3= U3/ R3= 72/60 = 1,2А






