В результате структурообразования свободнодисперсная система переходит в связнодисперсную. Появление и характер структур, как правило, определяются по изменению механических свойств, таких как вязкость, упругость, прочность, пластичность. Так как эти свойства непосредственно связаны со структурой тел, их называют структурно-механическими. Структурно-механические свойства могут быть изучены методами реологии - науки о деформациях и течении материальных систем.
Согласно закону Ньютона напряжение сдвига Р пропорционально скорости деформации 
(8.1)
Частным случаем приложения уравнения Ньютона к течению является уравнение Пуазейля, имеющее вид:
(8.2)
где V – объем жидкости, вытесненной через капилляр радиусом r и длиной l при разности давлений на концах капилляра Р за время t, r - плотность жидкости, h - вязкость.
Твердообразные дисперсные системы или пластические жидкости подразделяют на бингамовские и небингамовские. При малом напряжении сдвига в них проявляется упругость и течение отсутствует. Течение начинается при достижении предела текучести Рт.
Уравнение Бингама имеет вид
(8.3)
Скорость деформации равна 0 при 
< т, а при 
> 
т, она возрастает с увеличением напряжения.
Напряжение Р состоит из двух составляющих: напряжения, необходимого для разрушения структуры и называемого пределом текучести, и напряжения (
- т), осуществляющего собственно течение. Величина 
называется пластической вязкостью. Графически она определяется ctg угла наклона прямой, выходящей из точки, соответствующей пределу текучести.
(8.4)
По физическому смыслу ньютоновская вязкость 
отличается от пластической вязкости . Между ньютоновской и пластической вязкостью существует соотношение, которое получается комбинированием уравнения Ньютона и Бингама
;
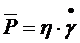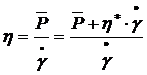(8.5)
В соответствии с уравнением Максвелла напряжение убывает со временем по закону
(8.6)
Величина 
имеет размерность времени и называется временем релаксации. Численно 
равно времени, в течение которого напряжение в образце уменьшается в е раз.
Вязкость жидких агрегативно устойчивых дисперсных систем всегда больше вязкости дисперсионной среды и увеличивается с увеличением объемной доли дисперсной фазы. Зависимость вязкости таких систем от объемной доли дисперсной фазы получена Эйнштейном. Он исходил из гидродинамических уравнений для микроскопических твердых сферических частиц, которые при сдвиге приобретают дополнительное вращательное движение. При этом рассеивается энергия, что является причиной повышения вязкости. Вязкость дисперсной системы зависит от объемной доли дисперсной фазы 
следующим образам:
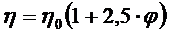(8.7)
где 
- вязкость дисперсионной среды.
При выводе уравнения предполагалось, что взаимодействие между частицами отсутствует, объемная концентрация частиц мала, частицы велики по сравнению со свободным пробегов молекул среды, но малы по сравнению с пространством, в котором происходит течение, смачивание частиц полное, распределение равномерное, течение ламинарное, силы инерции малы. Уравнение Эйнштейна было подтверждено экспериментально. Оказалось, что коэффициент при зависит от формы частиц. В общем виде уравнение имеет вид:
(8.8)
где a - коэффициент, зависящий от формы частицы.
После преобразований 
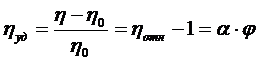(8.9)
Наиболее важный вывод из этого уравнения состоит в том, что разбавленные и устойчивые дисперсные системы являются ньютоновскими жидкостями, вязкость которых линейно увеличивается с объемной концентрацией дисперсной фазы и не зависит от дисперсности.
Уравнение Эйнштейна не учитывает наличия у частиц поверхностных слоев, таких как адсорбционные, сольватные и двойные электрические слои. Увеличение вязкости в таких случаях называют адсорбционным, сольватным и электровязкостным эффектами. Так как поверхностные слои не изменяют формы частиц, их влияние можно учесть путем увеличения объемной концентрации на величину объема слоев.
Зависимость вязкости от напряжения сдвига жидкообразных систем в логарифмических координатах показана на рис. 7. Свойства таких систем могут быть охарактеризованы тремя значениями вязкости.
Вязкость h0 называется наибольшей ньютоновской вязкостью. На этом участке течению подвергается система с неразрушенной структурой. Точнее говоря, при этих значениях напряжение сдвига
Рис. 7. Зависимость вязкости от напряжения сдвига
скорость разрушения структуры равна скорости ее восстановления. Явление течения без разрушения структуры называется ползучестью. Величина 
характеризует эффективную или пластическую вязкость, уменьшающуюся с увеличением напряжения сдвига. При этом происходит необратимое разрушение структуры дисперсной системы. Величина 
называется наименьшей ньютоновской вязкостью и характеризует течение системы с полностью разрушенной структурой. Проявление структуры и ее прочность можно охарактеризовать не только пределом текучести, но и разностью 
. Чем больше эта разность, тем прочнее структура материала.
Значения вязкости и могут отличаться на несколько порядков. Например, для 10%-ной суспензии бентонитовой глины в воде 
, 
.
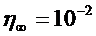
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
I. Вычислите вязкость ньютоновского коллоидного раствора по заданным величинам объемной доли твердой фазы jт а, толщины защитной оболочки d, вязкости дисперсионной среды h или одну из этих величин по известной вязкости раствора.
РЕШЕНИЕ Задача решается подстановкой известных величин в формулу Эйнштейна (8.7) или ее модификацию с учетом взаимосвязи между объемной долей твердой фазы 
и эффективной объемной долей частиц j вместе с защитной оболочкой, толщина которой равна d
Например, пусть заданы величины , а, 
и из опыта известна вязкость . По формуле (8.7) вычисляют и из сравнения j и 
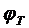находят толщину оболочки d.
2. Рассчитайте толщину гидратных оболочек 
водного золя Al2O3 если установлено, что при концентрации 12% маc. золь является ньютоновской жидкостью с вязкостью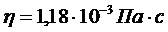 
. Радиус частиц золя равен 
; плотность частиц дисперсной фазы 
; дисперсионной среды 
; вязкость дисперсионной среды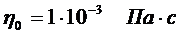 
; коэффициент формы частиц 
.
РЕШЕНИЕ По уравнению Эйнштейна 
, где
- объемная доля дисперсной фазы с учетом гидратации.
Объемная доля дисперсной фазы без гидратных оболочек равна:
Если n - число частиц в единице объема, то
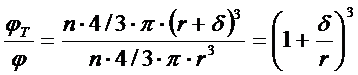
Откуда
