Электрокинетические явления, наблюдаемые в дисперсных системах, представляют собой относительное смещение фаз под влиянием внешнего электрического поля (электроосмос, электрофорез), либо возникновение разности потенциалов при относительном движении фаз, вызываемом гидродинамическими силами (потенциал течения, потенциал седиментации). Электрофорезом называется движение частиц дисперсной фазы относительно дисперсионной среды под действием внешнего электрического поля. Значение электрокинетического потенциала, возникающего при электрофорезе, можно рассчитать по уравнению Гельмгольца-Смолуховского:
 (5.1)
(5.1)
где h - вязкость среды;
u - скорость электрофореза;
e - диэлектрическая проницаемость среды;
E – напряженность внешнего электрического поля;
e0 - электрическая постоянная, равная 8,85 .10-12 ф/м.
Значения e и h, подставляемые в уравнение Гельмгольца-Смолуховского, берутся обычно для дисперсионной среды. Для воды при комнатной температуре можно с достаточной точностью принять, что e= 81, а h = 0,001 Па×с.
При электрофорезе на поверхности электрода происходит образование осадка, масса которого зависит от характера электрического поля. При осаждении в неоднородном электрическом поле, заданном системой двух соосных цилиндров, массу осадка m, образующегося на центральном электроде за время t, рассчитывают по формуле
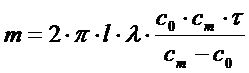 (5.2)
(5.2)
где
 (5.3)
(5.3)
где U – разность потенциалов;
x - электрокинетический потенциал;
l - длина покрытой части электрода;
c0 – концентрация суспензии;
сm- концентрация суспензии в предэлектродной зоне;
r1 и r2 – радиусы цилиндрических электодов;
e - диэлектрическая проницаемость среды;
e0 - электрическая постоянная, равная 8,85 .10-12 ф/м.
Электроосмос - это движение жидкости (дисперсионной среды) относительно неподвижной дисперсной фазы (капиллярно-пористых материалов, диафрагм) под действием внешнего электрического поля. Из условия стационарного режима электроосмотического движения жидкости в плоском капилляре Смолуховский получил уравнение, связывающее скорость течения жидкости и x-потенциал:
 (5.4)
(5.4)
где h - вязкость жидкости;
u – линейная скорость течения;
e - диэлектрическая проницаемость;
E – напряженность внешнего электрического поля;
e0 - электрическая постоянная, равная 8,85 .10-12 ф/м.
Для практического применения более удобна формула, в которую входят величины, измеряемые непосредственно в опыте. Ее можно получить, если выразить линейную скорость u через объемную v, а Е - через силу тока:
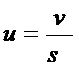 (5.5)
(5.5)
 (5.6)
(5.6)
В уравнениях (5.5) и (5.6)
r – удельное сопротивление;
U – внешняя разность потенциалов;
I - сила тока;
R – электрическое сопротивление;
L – расстояние между электродами;
c - удельная электрическая проводимость.
Подставив (5.5) и (5.6) в (5.4) получим расчетную формулу 
 (5.7)
(5.7)
Добавочная удельная электрическая проводимость жидкости в капиллярной системе по сравнению с жидкостью вне её называется поверхностной проводимостью cs. При расчете величины x с учетом поверхностной проводимости в уравнение (5.7) вводится коэффициент активности диафрагмы a:
 (5.8)
(5.8)
где
 (5.9)
(5.9)
При течении жидкости через пористую диафрагму под влиянием приложенного давления по длине диафрагмы возникает разность потенциалов, называемая потенциалом течения. Потенциал течения выражается следующим уравнением:
 (5.10)
(5.10)
где Р - давление, вызывавшее течение жидкости.
При оседании дисперсных частиц в гравитационном поле двойные электрические слои, окружающие частицу, деформируются за счет трения о слой жидкости. В результате этого диффузные ионы отстают от движущихся частиц и по высоте оседания возникает разность потенциалов, называемая потенциалом седиментации Uсед.
Связь между потенциалом седиментации и электрокинетическим
потенциалом можно установить из уравнения (5.10), заменив давление
Р силой тяжести F g, вызывающей седиментацию частиц.
Сила тяжести
 (5.11)
(5.11)
где φ - объемная доля дисперсной фазы, равная для сферических частиц радиуса r: 4/3ּπּr3ּn,
n - число частиц в единице объема;
ρ и ρ0 - плотности дисперсной фазы и дисперсионной среды;
g - ускорение свободного падения.
 (5.12)
(5.12)
Электрокинетические явления широко используются в науке и технике. Наибольшее их практическое применение связано с нанесением покрытий на различные поверхности электрофоретическим методом. Данный метод позволяет получать равномерные покрытия на деталях сложной конфигурации благодаря его высокой кроющей способности.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. Вычислите величину дзета-потенциала на границе кварцевое стекло - водный раствор КСl. Процесс электроосмоса характеризовался следующими данными: сила тока равна 4·10-4 А; время переноса 10-8 м3 раствора КС1 равно 12,4 с; удельная электропроводность среды 1,8·10-2 Ом-1 м-1; вязкость среды равна 1·10-3 Н·с/м2; диэлектрическая проницаемость среды 81.
РЕШЕНИЕ Связь дзета-потенциала с электроосмотической объемной скоростью v м3/с выражается уравнением (5.7):

Вычисляем объемную скорость электроосмоса
 м/с,
м/с,
тогда
 В.
В.
2. Под каким давлением должен продавливаться раствор КС1 через керамическую мембрану, чтобы потенциал течения был равен 4 .10-3 В? Дзета-потенциал без учета поверхностной проводимости равен 3 . 10-2 В, электропроводность – 1,3 . 10-2 Ом-1 м-1, диэлектрическая проницаемость среды 81, вязкость среды 1 . 10-3 Н . с/м2.
РЕШЕНИЕ Из формулы (5.10) без учета поверхностной проводимости

следовательно
 Н/м2 .
Н/м2 .
3. Найдите величину дзета-потенциала для суспензии кварца в воде. При электрофорезе частицы перемещаются к аноду; смещение границы составило 5 . 10-2 м за 30 мин; градиент напряжения внешнего поля равен 103 В/м; диэлектрическая проницаемость среды 81; вязкость среда 1 . 10-3 Н . с/м2.
РЕШЕНИЕ Расчет дзета-потенциала по скорости электрофореза ведется по формуле (5.1):

Рассчитываем скорость электрофореза
 м/с,
м/с,
тогда
 В.
В.
4. Рассчитайте x-потенциал диафрагмы из частиц глины в растворе хлорида натрия с учетом поверхностной проводимости по следующим данным: c = 2,5.10-2 Ом-1.м-1; n = 1,2 . 10-8 м3/c; æs = 1,65. 10-2 Ом-1. м-1; h = 1 . 10-3 Па . с; I = 1,2 .10-2 А; e = 81.
РЕШЕНИЕ По формуле (5.9) рассчитывают коэффициент эффективности диафрагмы:
 .
.
Затем по формуле (5.8) рассчитывают ξ-потенциал с учетом поверхностной проводимости:
 В.
В.
5. Рассчитайте массу осадка, полученного на цилиндрическом электроде при электрофорезе водной суспензии карбоната стронция. Длина электрода l = 2.10-2 м; радиус внутреннего электрода r2 = 1.10-3 м; радиус наружного электрода r1 = 24.10-3 м; ξ = 35.10-3 В; напряжение на электродах U = 15 B; c0 = 0,7 . 103 кг/м3; η = 1.10-3 Па.с; cm = 1.103 кг/м3; ε = 81; τ = 20 c.
РЕШЕНИЕ По уравнениям (5.2) и (5.3) рассчитывают λ и массу электрофоретического осадка (m):
 м2/c;
м2/c;
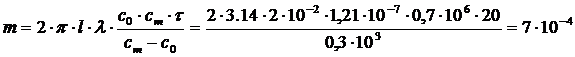 кг.
кг. 
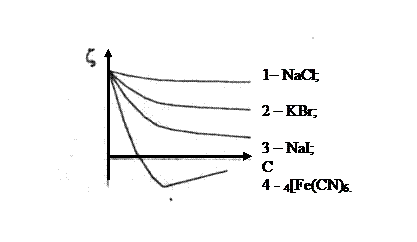
6. Напишите формулу мицеллы золя Sb2S3, cтабилизированного SbCl3 и изобразите графически зависимость x=¦(с) при введении электролитов: NaI, NaCl, K4[Fe(CN)6, KBr.
РЕШЕНИЕ Формула мицеллы золя: {m Sb2S3 n Sb3+ 3(n-x)Cl-} 3xCl-. Перечисленные электролиты являются индифферентными по отношению к данному золю.