ДИСПЕРСИОННЫЙ АНАЛИЗ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ ВЕЛИЧИН
Проверка гипотезы о нормальном распределении случайной величины при помощи модифицированного критерия χ2
Краткая теория, справочные таблицы и основные уравнения изложены в [1].
Задача №1: Имеется ряд выборочных значений случайной величины (n=100):
Ряд 1 43 76 84 91 95 101 105 114 122 129
Ряд 2 54 77 84 91 96 101 106 114 122 132
Ряд 3 56 77 85 91 96 101 107 115 122 134
Ряд 4 57 78 85 91 96 103 107 116 123 136
Ряд 5 61 78 86 92 97 103 107 116 124 136
Ряд 6 64 79 87 92 97 104 108 116 124 138
Ряд 7 67 79 87 93 98 104 111 117 125 143
Ряд 8 73 82 87 93 98 104 112 118 125 143
Ряд 9 74 82 88 93 99 104 113 118 125 145
Ряд 10 76 83 89 95 101 105 114 119 126 150
Необходимо проверить модифицированным критерием χ2 на уровне значимости α = 0,1 гипотезу нормальности распределения при оценке его параметров по негруппированным данным.
Решение
Имеем 
Из таблицы 4.1 [1] находим коэффициенты разбиения (принимаем k=10): с1=-1,2816; с4=-0,2533; с7=0,5244; с2=0,8416; с5=0; с8=0,8416; с3=0,5244; с6=0,2533; с9=1,2816. Для условий задания коэффициенты не изменятся.
Границы интервалов определяются следующим образом:
следует помнить, что с0=-∞ и сk=∞.
Определим количество членов выборки попавшее в i-й интервал. Результаты расчетов сведем в таблицу 1.
Таблица 1
Результаты обработки выборочных значений
| Границы интервалов | 
| 
|
| 1 2 3 4 5 6 7 8 9 10 | -∞  72,79
72,79 82,40
82,40 89,32
89,32 95,24
95,24 100,77
100,77 106,30
106,30 112,22
112,22 119,14
119,14 128,40
128,40 ∞
| 7 12 11 11 8 13 6 12 10 10 | 49 144 121 121 64 169 36 144 100 100 |
|
| 100 | 1048 | |
Статистика критерия равна:
χ2= 
Из таблицы 4.2 [1] находим критическое значение статистики для k=10 и α=0,1: d10(0,1)=12,384. Так как χ2=4,8<d10(0,1)=12,384, гипотеза нормальности исходного распределения вероятностей не отклоняется.
Варианты заданий
Принять ряд выборочных значений случайной величины (n=100) по примеру заменив значения величин в рядах согласно таблице 1.
Таблица 1 – Исходные данные
| № вар. | Ряд | ||||||||||
Значение случайной величины
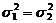против альтернативы: 
при доверительной вероятности α=0,95.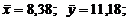
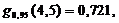нулевая гипотеза не отклоняется.
