Выражения и оператор присваивания в AnyLogic

Выражение возвращает значение некоторого типа. Выражение обычно явля­ется частью некоторой большей конструкции, чаще всего правой частью оператора присваивания. В модели AnyLogic в окне свойств объектов (ак­тивных объектов, состояний и переходов стейтчартов, элементов анимации и т. п.) существуют поля, в которые может быть помещено только выраже­ние, возвращающее значение определенного типа. Например, в поле дина­мического значения текста должно появиться выражение, возвращающее строку символов, в поле Условие перехода стейтчарта может стоять выраже­ние, возвращающее в результате своего выполнения булевское значение, в поле для указания цвета элемента анимации может стоять выражение, воз­вращающее значение типа color, и т. п. Никаких разделителей после таких выражений не нужно, их включение приведет к синтаксической ошибке.

Во всех местах, где можно написать выражение, может быть использовано и условное выражение.

В отличие от выражения, оператор присваивания (=) — это действие, со­стоящее в вычислении значения выражения, стоящего в правой части опе­ратора присваивания, объекту, стоящему в левой части оператора. Операто­ры присваивания в моделях AnyLogic обычно записываются в полях, относящихся к действиям, связанным с наступлением некоторого события. Тип объекта в левой части оператора присваивания должен совпадать с ти­пом результата, возвращаемого выражением в правой части этого оператора.

Сложные типы данных

В качестве более сложных, непримитивных типов данных в Java, мы рас­смотрим строки, тип color и массивы.

Строки

Строки — это последовательности символов, например, "Hello". Строки за-даются стандартным образом — объявлением типа и именем:

String greeting; Greeting = "Hello";

Здесь greeting — переменная типа string, которая при выполнении второ­го оператора присваивания получит значение этого типа — строку символов

"Hello". До выполнения этого оператора вновь объявленное значение этой

переменной не определено.

При объявлении типа переменной ей может быть сразу присвоено значение

String е = "";

Соединение двух строк (конкатенация) обозначается знаком +, например:

String name = "John";

String greeting = "Hello";

String message = "Hello" + ", " + name;

В результате message получит значение "Hello, John".

Если выполняется операция конкатенации строки с объектом, не являю­щимся строкой, тип этого объекта неявно конвертируется в строку. Таким образом, если delta — переменная целого типа со значением 256, то:

String message = "Delta = " + delta;

определяет строку с именем message, которая при выводе даст:

Delta = 256

Строки используются в моделях AnyLogic, в частности, для вывода текста и численных значений. Для вывода в окне анимации определяется текст, и строка записывается в поле динамических значений этого текста окна его свойств. В это поле может быть помещена любая конструкция типа string, например заданная условным выражением:

"Опасность:"+((Т>30)?"Большая":(Т>20)?"Средняя":"Малая")

Если delta — переменная нестрокового типа, то следующее определение, однако, будет ошибочным:

String message = delta;

Здесь необходимо использование пустой строки, к которой с помощью кон­катенации присоединяется нестроковый объект. Этот объект будет неявно конвертирован в строковое представление:

String message = ""+delta;

В AnyLogic при компиляции модели в программу на Java текст, находящий­ся в поле динамического значения текста, автоматически предваряется тре­мя символами, двумя кавычками и плюсом: ""+. В результате, в этом поле может быть записан и любой нестроковый объект, например число или вы­ражение, которое присоединяется операцией конкатенации к пустой строке и поэтому неявно конвертируется в символьное представление.

Отладочная печать

В качестве одного из операторов (в тексте какой-либо функции либо в поле Действие, связанном с некоторым событием) в модели может быть помещен вызов функции:

traceln(<любая строка>);

При вызове этой функции происходит печать строки в окне Глобальный журнал. Например, выполнение кода:

traceln("Переход tl, переменная s =" + s);

помещенного в поле Действие какого-либо перехода стейтчарта модели, вы­зовет печать в журнале строки:

Переход tl, переменная s = 23.99

как только данный переход действительно сработает, и при этом значение переменной s будет равно 23.99. Такими контрольными выводами можно пользоваться при отладке модели.

7.2.3. Тип Color

Color — это тип данных. В качестве констант данного типа в языке Java определены 13 базовых цветов:

black, blue, white, green, cyan, magenta, gray, lightGray, darkGray, orange, pink, red, yellow

Обратиться к базовому цвету можно обычным образом, как к константам

Класса Color, а именно: Color.black, Color.blue, Color.white И Т. П.

Задание статического значения цвета графического элемента модели

В моделях на AnyLogic цвет используется в анимации. Чтобы для графиче­ского элемента задать статический цвет его заливки или граничной линии, используется выпадающее меню окна свойств этого графического объекта.

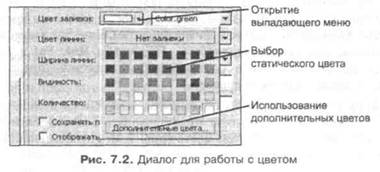
В случае если имеющиеся в появившейся палитре цвета не подходят, с по­мощью кнопки Дополнительные цвета можно открыть окно стандартного системного диалога работы с цветом (рис. 7.3).

С помощью этого окна простым щелчком мыши по выбранной клетке на палитре слева можно выбрать любой желаемый цвет для представления

в поле статического значения цвета выделенного графического элемента мо­дели на AnyLogic. Если и этих цветов не хватает, то используется двумерная палитра справа.

Существует несколько моделей для определения цвета. Диалоговое окне рис. 7.3 поддерживает две из них, модель HSL и модель RGB. Модель HSL (Hue, Saturation, Luminosity — тон, насыщенность, яркость) представлена в этом окне двумерной палитрой по координатам Hue, Saturation и отдель­ным столбцом, управляющим яркостью. Параметры Hue, Sat и Lum могут принимать целые значения в соответствии с палитрой, представленной в системном диалоговом окне справа.

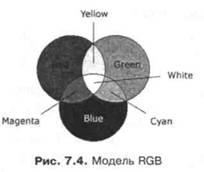
Модель RGB использует три базовых цвета, Red, Green и Blue (красный, зеленый и синий), которые могут присутствовать с определенной интен­сивностью в каждом конкретном цвете (рис. 7.4). Интенсивность каждого из трех базовых цветов ранжируется от 0 до 255 и представляется целым числом. Различные комбинации максимальной интенсивности этих базо­вых цветов позволяют представить дополнительные цвета.

Цвет, выбранный в окне диалога рис. 7.3, представляется в нижней правой части этого окна тремя параметрами как для модели HSL, так и для модели RGB. Например, интенсивности трех базовых цветов для цвета Yellow в мо­дели RGB имеют следующие значения: (255, 255, 0).

Задание динамического значения цвета графического элемента модели

Для задания динамического значения цвета (если оно отличается от стати­ческого) в соответствующее поле должно быть помещено выражение типа Color. Данное выражение может состоять из единственной константы этого типа (можно использовать любую из 13 констант, перечисленных в выпа­дающем меню). Кроме того, цвет может задаваться условным выражением. Например, пусть цвет графического элемента, который должен отображать­ся в анимации при выполнении модели, нужно сделать либо красным, либо синим в зависимости от того, превышает ли переменная power заданный порог threshold. Для этого в поле для динамического значения цвета окна свойств этого элемента нужно записать: power > threshold? Color.red: Color.blue

В качестве выражений, помещаемых в поле динамического значения цвета, можно использовать также любые функции, возвращающие зна­чение типа color. Две такие функции new color (<r>,<g>,<b>) и lerpColor(<val>,colori,color2) указаны в выпадающем меню поля динами­ческого значения цвета каждого графического элемента модели на AnyLogic.

Функция new color (< r >, < g >, < B >) порождает цвет в соответствии с моделью RGB. Как указывалось ранее, параметры <R>, <G> и < B > могут быть целыми константами в пределах от 0 до 255 либо переменными целого типа, изме-нЯЮЩИМИСЯ в этих же пределах. Выбрать эти параметры для конкретного цве-та можно с использованием показанного ранее окна стандартного системного диалога работы с цветом: для этого следует поместить указатель на двумерной палитре в координатах Hue и Sat, после чего выбрать яркость, передвигая мышью указатель столбца Luminance. Значения параметров < r >, < g > и <B> выбранного цвета появятся в правом нижнем углу диалогового окна.

Если требуется порождение графических элементов с произвольным случайно выбранным цветом, то для этого можно использовать функцию color, целые параметры которой выбираются случайно среди чисел от 0 до 255.

Построим три примера моделей, работающих с цветом.

Выбор цвета в модели RGB

Построим простую модель, в которой цвет графического элемента будет определяться тремя параметрами: Red, Green и Blue, изменяемыми поль­зователем.

Создайте новый проект ColorModel. В окне редактора корневого активного объекта Main введите три целые параметра с именами Red, Green и Blue с нулевыми начальными значениями. Введите новую анимацию, в которой постройте прямоугольник с произвольной статической начальной заливкой цветом. В поле динамического значения цвета заливки этого прямоугольни­ка введите выражение new Color (Red, Green, Blue). В поле анимации также введите три слайдера (ползунка). Каждый из них должен управлять своим па­раметром (Red, Green или Blue) в диапазоне от 0 до 255. Запустите модель на выполнение по шагам (): поскольку наша модель не динамическая, нам

достаточно только построения начального состояния анимации. В открыв­шемся окне анимации модели вы увидите результат, похожий на рис. 7.5.

Изменяя значения параметров с помощью ползунков, вы будете наблюдать соответствующее изменение цвета заливки прямоугольника. Введите подписи на анимации так, чтобы идентифицировать параметры и их значения. Срав­ните свою модель с моделью colorModel0 в папке Model Examples\Part II.

Палитра RGB

Построим другую модель, которая показывает изменение палитры цветов для RGB-модели так, что две координаты палитры, х и у, будут представ­лять значения параметров Red и Green, а значение третьего параметра Blue будем задавать с помощью слайдера. Кроме того, пусть от установленного значения при работе модели параметр Blue меняется на единицу через каж­дый шаг модельного времени.

Создайте новый проект colorModel1. В окне редактора объекта Main введите целую переменную в и статический таймер, который будет работать цикли­чески и при срабатывании увеличивать значение в на 1 по модулю 256. Для этого в поле Действие при срабатывании в окне свойств таймера поместите два оператора:B++ B %= 256;

Инкремент (в++) при каждом срабатывании таймера увеличивает в, а опера­ция B %= 2 56 дает остаток по модулю 256.

Построим в поле анимации двумерную палитру цветов так, чтобы по оси X изменялось значение параметра R, а по оси Y изменялось значение парамет­ра G. Каждому набору значений координат X и Y поставим в соответствие прямоугольник размером 1x1 пиксел с цветом, определяемым функцией new color(x, у, в), где х и у — координаты прямоугольника, а в — перемен­ная, заданная отдельно и изменяемая таймером. Введите в модель новую анимацию. В окне редактора анимации переверните ось Y, чтобы она смот­рела вверх. Для штриховой рамки, ограничивающей изображение, установи­те следующие параметры: X = -100, Y = 350, Ширина = 500, Высота = 450. Введите в поле анимации произвольный прямоугольник, который будет представлять один пиксел — минимальный графический элемент, имеющий фиксированный цвет. Для этого в полях динамического значения ширины и зысоты прямоугольника установите 1, а число таких прямоугольников в поле Количество окна свойств прямоугольника определите как 256*256 (рис. 7.6).

В поля динамических значений координат X и У окна свойств прямоуголь­ника поместите:

X: index % 2 56

Y: index / 256

При таком определении весь массив прямоугольников размером 1x1 распо­ложится в квадрате 256*256, координаты X и Y (верхних левых) углов этих

прямоугольников будут иметь следующие значения. У первых 256 прямо­угольников координата X будет меняться от 0 до 255, а их координата Y бу­дет равна 0. Следующие 256 прямоугольников будут иметь координату равную 1, а координаты X также будут пробегать значения от 0 до 255 и т. я

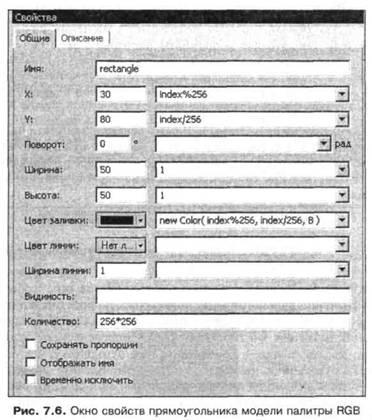
Цвет линии границы установите Нет линии, а динамическое значение цвета заливки прямоугольников определите как:

new Color(index%256, index/256, В)

Ясно, что по координате X все прямоугольники будут иметь параметр < R > функции new color (< r >,< g >,<в>), изменяющийся от 0 до 255, а по коорди­нате У все прямоугольники будут иметь значение параметра <g>, изменяю­щегося также от 0 до 255 в соответствии с координатами прямоугольника.

Для изменения начального значения переменной в введите вертикальный слайдер (ползунок), который меняет ее значение от 0 до 255. Анимация мо­дели должна выглядеть похожей на рис. 7.7.

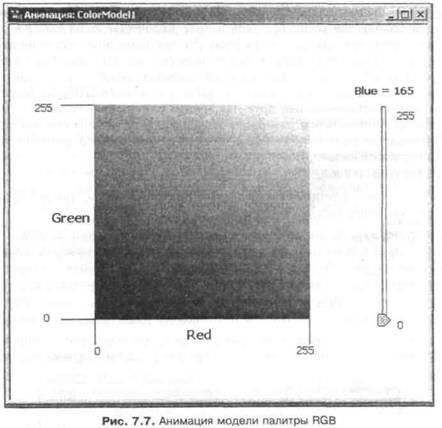
Остальные графические элементы анимации (отрезки прямых и поясняю­щие тексты) введите в соответствии с рис. 7.7. Сравните вашу модель с мо­делью ColorModel1 папки Model Examples\Part II.

Функция lerpColor

Функция:

lerpColor(<value>, color1,color2)

выдает промежуточное значение цвета, между color1 и color2, в зависимо­сти от значения вещественного параметра value. Если значение value меньше или равно 0, то результат функции — coiori, если значение value больше или равно 1, то результат функции — color2. Промежуточные зна­чения value между 0 и 1 определяют промежуточный цвет.

Для большего понимания того, как работает эта функция, построим про­стую модель. Создайте новый проект colorModel2 и введите в модель новую анимацию. В окне редактора анимации переверните ось У, чтобы она смот-

рела вверх. Далее, нарисуйте в поле анимации горизонтальный отрезок линии и количество таких отрезков в поле Количество окна свойств этого отрезка определите, например, равным 201 (их нумерация будет пробегать значения от 0 до 200). Динамическое значение координаты X введенного отрезка оставьте пустым, а динамическое значение координаты Y определи­те просто как index. Это будет означать, что в модели будет порожден 201 отрезок, расположенный друг над другом с Y-координатами 0, 1, 2,.... 200. Цвет линий выберем разным, в зависимости от номера отрезка линии (номер задается параметром index). В поле динамического значения цвета линии поставьте вызов функции: lerpColor(index/200., Color.blue, Color.magenta)

(заметьте, чтобы получить первый параметр вещественным, число 200 пред­ставлено как вещественная константа).

Создайте несколько копий определенного так графического элемента (на­пример, переместите этот элемент горизонтально при нажатой клавише <Ctrl> клавиатуры). У всех копий измените только второй и третий пара­метры функции lerpColor. Например, у одной копии поставьте color.гed И Color.green, у другой Color.orange И Color.gray И Т. П. Запустите мо­дель на выполнение по шагам (): поскольку наша модель не динамиче­ская, нам достаточно только построения начального состояния анимации. В открывшемся окне анимации модели вы увидите результат, похожий на рис. 7.8.

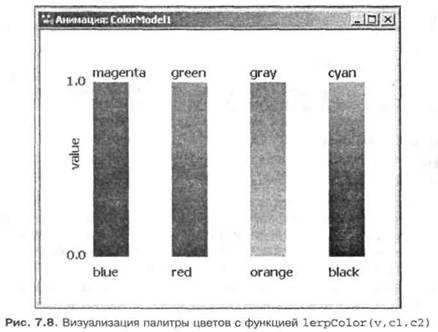
Введите подписи на анимации так, чтобы идентифицировать пары цветов. Сравните свою модель с моделью colorModel2 в папке Model Examples\ Part II.

Массивы

В модели на AnyLogic переменные вводятся с помощью кнопки панели инструментов. Введенные таким образом переменные могут представлять не только простую скалярную переменную, ее можно определить как матрицу или многомерный массив. Для прямоугольных матриц и одномерных масси­вов AnyLogic предоставляет удобные средства их определения и работы с ними как с едиными объектами. В список операций над матрицами в AnyLogic входят все основные операции линейной алгебры, для выполне­ния таких операций нет необходимости использования каких-либо управ­ляющих конструкций Java, например циклов. Операции над многомерными массивами, определенными как переменные AnyLogic матричного типа, выполняются с целым объектом, например скалярное умножение скаляр­ной величины с на матрицу а определится как с*а, сложение двух матриц а и в запишется как а+в и т. п.

В AnyLogic возможно также использование массивов языка Java. Массив в Java — это набор объектов одного и того же (произвольного) типа, на ко­торые ссылаются по общему имени, а различают отдельные элементы мас­сива по номеру (индексу). Индексация массивов начинается с нуля, поэтому последний элемент массива из N элементов будет иметь индекс n-1, а пер­вый — индекс о.

Одномерный массив — это просто список однотипных объектов. Построение массива включает два этапа. Во-первых, нужно объявить переменную мас­сива с указанием типа элементов массива. Общий формат объявления мас­сива:

<тип> <имя переменной> [ ];

Здесь <тип> объявляет базовый тип массива (т. е. тип объектов, которые данный массив будут составлять), <имя переменной> — имя переменной это­го массива, например: int count [ ];

После такого объявления массива с именем count еще не существует, поро­ждается только массив "без значения". Чтобы связать имя count с фактиче­ским массивом целых, нужно выполнить второй этап — выделение памяти для массива. Для этого используется операция new, для которой нужно ука­зать имя и число элементов массива: count = new [<размер>];

Эта операция выделит для массива память и инициализирует все элементы массива нулями. Например, после операции

count = new [10];

можно обращаться к элементам массива count по номерам, от count [о] до count [9], например, инициализировать их:

count[0] = 5; count[1] = 7;

Аналогично тому, как это делается при объявлении переменных простых типов, возможна комбинация объявлений переменной массива с выделени­ем массиву памяти. Например, объявление массива из десяти целых с выде­лением ему памяти:

int count[] = new int [10];

Альтернативно, для удобства, объявление массива может быть сделано и так:

int[ ] count;

и объявление с порождением массива так:

int [ ] count = new int [10];

Многомерные массивы

В Java многомерные массивы — это массивы массивов. Для объявления мно­гомерной переменной нужно определить каждый дополнительный индекс, используя свой набор квадратных скобок. Например, следующий оператор объявляет переменную neighbors как двумерный массив 4x5 целых:

int neighbors [] [] = new int [4] [5];

Как и в одномерном массиве, наименьшее значение индексов здесь 0, мак­симальное значение у первого индекса 3, у второго 4.

Альтернативная форма объявления многомерного массива допустима и здесь:

int[][] neighbors = new int [4] [5];

Динамические массивы

Во многих языках программирования (и в том числе, в Java) вы должны за­фиксировать размеры всех массивов в момент компиляции. Во многих слу­чаях это неудобно. Часто в моделях желательно создавать и уничтожать эк­земпляры некоторых классов динамически, во время работы модели. Например, это относится к реплицированным объектам AnyLogic. Динами­ческое создание и уничтожение объектов является одной из главных кон­цепций в многоагентном моделировании, которое мы рассмотрим в главе 15.

В языке Java существует тип vector, который позволяет создавать динамиче­ские массивы объектов любой природы, т. е. массивы, число элементов в ко-торых может меняться при выполнении программы. Фактически, экземпля­ры вектора являются контейнерами, в нем могут храниться объекты любого типа. Поэтому тип объектов, которые хранятся в векторе, является наиболее общим, предполагается, что все хранящиеся в векторе объекты имеют тип Object.

Название vector является несколько дезориентирующим, поскольку в Java векторы не имеют ничего общего с векторами, используемыми в математике и физике. Математические вектора — это упорядоченные массивы одного и того же типа. Вектора в Java — это упорядоченные списки объектов произ­вольных типов.

Создать новый вектор можно просто, даже не задавая его начальную ем-кость:

Vector v = new Vector ();

После такой инициализации вектор еще не содержит элементов. Туда их следует добавить явно. Мы рассмотрим работу с векторами далее на приме­ре манипулирования реплицированными (размноженными) объектами. Именно векторы используются для хранения реплицированных экземпляров объектов в AnyLogic.

Функции

Как и во всех языках программирования, в Java можно разбить сложную задачу выполнения вычислений на более простые подзадачи, называемые традиционно функциями. В Java, как и в других объектно-ориентированных языках, функции называются методами. Мы далее будем использовать как то, так и другое название. Как будет видно далее, классы — основные струк-турные блоки объектно-ориентированного программирования — состоят из двух видов компонентов, из переменных и методов.

Вызов методов классов

Для вызова метода указывается имя метода, после которого следуют скобки. Если метод имеет параметры, они перечисляются в скобках через запятую. Из любого места модели AnyLogic можно обращаться к методам, перечис­ленным в классе Func в справочнике классов AnyLogic. Примерами методов этого класса являются:

- математические функции: sqrt, sin, cos, tan, exp, log, round и др.; - функции для работы с матрицами: add, mul, inverse, transpose и др.; - функции-генераторы случайных чисел: uniform, exponential и др.

В ЭТОТ класс также ВХОДЯТ системные функции getTime, getOwner, getRoot

isStateActive И Т. П.

Например, выполнив оператор x=getTime() в любом месте модели, мы по­лучим в переменной х вещественное значение текущего времени.

7.3.2. Функции: методы класса, определенные пользователем

При создании нового класса пользователь может добавить свои методы. В AnyLogic есть несколько способов определения функций как составных частей активных объектов. В каждый активный объект можно добавить но­вые функции с помощью иконок: табличную функцию (), арифметиче­скую функцию () и алгоритмическую функцию (). Кроме того, в каж­дом объекте AnyLogic, который компилируется в класс (кроме активных объектов это порты, анимация, стейтчарты и т. п.), можно также определить функции в общей форме. Рассмотрим все их по порядку.

Табличная функция

Этот вид функции используется в случаях, когда зависимость от аргумента задается с помощью конечной таблицы соответствия оначение аргумента, значение функции>. AnyLogic предоставляет удобные средства для задания этих пар, а также для определения типа интерполяции функции (способа определения функции в промежутках между заданными значениями аргу­мента) и экстраполяции их (закона определение значений функции вне ин­тервала определения аргументов). Функция вводится с помощью кнопки  панели инструментов при выделенном активном объекте или выбором команды Новая табличная функция в контекстном меню активного объекта.

Математическая функция

Математическая функция в активном объекте используется в случаях, когда зависимость от аргументов задается одним арифметическим выражением, включающим обычные математические функции, а также переменные, па­раметры и функции, определенные пользователем в данном активном объ­екте. Здесь нельзя использовать условное выражение. В AnyLogic математи­ческая функция вводится с помощью кнопки панели инструментов при

выделенном активном объекте либо выбором команды Новая математиче­ская функция в контекстном меню активного объекта. Использование кноп­ки Мастер позволяет при наборе кода определения функции в поле Тело функции автоматически включать уже определенные функции и параметры, а также стандартные функции.

Алгоритмическая функция

Этот вид функции используется в случаях, когда зависимость от аргументов нельзя выразить одним простым арифметическим выражением, а требуется использовать более сложные конструкции. В AnyLogic такая функция вво­дится с помощью кнопки панели инструментов при выделенном актив­ном объекте либо выбором команды Новая алгоритмическая функция в кон­текстном меню активного объекта. В поле Тело функции записывается алгоритм, в котором должны встретиться операторы вида: return <выражвние>

Этот опрератор выполняется последним, возвращая как результат выполне­ния функции значение выражения.