Из общих условий термодинамического равновесия (1-20), (1-21) следует, что сосуществование двух фаз чистого вещества (твердой и жидкой, твердой и газовой, жидкой и газовой1) осуществляется вдоль соответствующей кривой сосуществования p е (Т) − парообразования р s (Т), плавления рпл (Т)или сублимации рс (Т), уравнение которой
1 Обычно газ, находящийся при Т<.Ткр, когда он может быть сконденсирован путем изотермического сжатия, называют паром. В гл. 1 и 2 мы пользуемся только первым из этих двух терминов, поскольку оба они обозначают одно и то же состояние вещества.
41
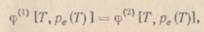(1-57)
где 
−удельная или мольная свободная энергия Гиббса фазы a. Уравнение (1-57) определяет также условие фазового равновесия между различными аллотропическими модификациями твердого вещества, если таковые имеются. Из (1-57) с учетом (1-10)нетрудно получить дифференциальное уравнение для кривой сосуществования − уравнение Клапейрона−Клаузиуса [3]:
(1-58)
где
(1-59)
− разность удельных (мольных) объемов сосуществующих фаз, а
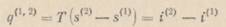(1-60)
− теплота фазового перехода: 
− теплота парообразования;
− теплота плавления; 
- теплота сублимации. Все эти три величины, разумеется, существенно положительны. Положительны и разности объемов 
и 
при парообразовании жидкости и сублимации твердого тела. Что касается величины 
, то, как уже указывалось, она положительна для нормальных (к ним относятся все криоагенты) и отрицательна для аномальных веществ.
Точка, в которой сосуществуют одновременно три фазы, называется тройной. Наиболее известна тройная точка сосуществования твердой, жидкой и газовой фаз:
(1-61)
В этой точке 
. Если твердое тело может находиться в различных аллотропических модификациях, возможны и тройные точки, отвечающие сосуществованию двух твердых фаз и жидкости или газа либо трех твердых фаз.
Кривая сублимации рс (Т)начинается в точке T =0, рс (0)=0 и заканчивается в тройной точке T тр, р тр. Из нее же исходят кривая плавления p пл (Т)и кривая парообразования р s (Т). Последняя заканчивается критической точкой Т к, рк, в которой свойства жидкости и газа становятся тождественными:
(1-62)
Вид типичных кривых сосуществования и характер изменения термодинамических свойств сосуществующих фаз вдоль этих кривых иллюстрируются в [3, 12].
На рис. 1-5 в качестве примера изображены кривые сосуществования фаз для вещества, претерпевающего в твердой фазе полиморфные превращения между аллотропическими модификациями a, b и g. Подобный характер имеет фазовая диаграмма важного криоагента − кислорода.
Уравнение Клапейрона−Клаузиуса (1-58) можно приближенно, проинтегрировать и найти явную зависимость упругости насыщенных паров над жидкостью р s (Т)и над твердой фазой р c (Т)от температуры. С этой целью будем считать, что r и l не зависят от Т, а 
и соответственно 
. Тогда получим:
(1-63)
где р о− стандартное давление, а T н.к − соответствующая ему нормальная температура кипения, и
(1-64)
Заметим, что условия фазового равновесия (1-57) можно было бы записать, используя летучести фаз (1-41):
| 
|
| Рис. 1-5. Кривые сосуществования фаз вещества с полиморфными превращениями в твердой фазе. | Рис. 1-6. Кривые сосуществования фаз Не4. |
В частности, если одна из фаз − идеальный газ, то с учетом (1-44) получим выражения для летучестей жидкости и твердого тела в точке равновесия:
(1-65)
Неидеальность газа легко учесть с помощью (1-45). При p >ре (Т),используя (1-42) и полагая, что объем у жидкости или газа не зависит от р, получаем приближенное выражение для летучести вещества в конденсированной фазе:
(1-66)
Существенной особенностью обладает фазовая диаграмма Не4, показанная на рис. 1-6. Это вещество остается жидким при 
МПа вплоть до Т= 0К. Причина этого эффекта чисто квантовая и связана с тем, что амплитуда «нулевых колебаний» атомов жидкого гелия превышает межатомные расстояния в узлах кристаллической решетки твердого Не4, так что она оказывается неустойчивой даже при Т= 0К. По той же причине остается жидким при р <3 МПа вплоть до T =0 К и другой изотоп гелия − Не3. Однако у этого изотопа имеется и другая интересная особенность − минимум на кривой плавления. Левее минимума теплота плавления Не3 оказывается отрицательной. Это явление носит название эффекта Померанчука [22].
Наряду с фазовыми переходами 1-го рода, которые мы выше анализировали, могут происходить и фазовые превращения, не сопровождающиеся объемным (1-59) и тепловым (1-60) эффектами, − фазовые переходы 2-го рода [3, 14]. Для таких превращений
(1-67)
однако в точке перехода ре (Т)скачкообразно меняются теплоемкость, изотермическая сжимаемость и термическое расширение.
Рис. 1-7. «l -точка» на кривой зависимости теплоемкости Не4 от температуры. Левая ветвь кривой (температура ниже Т) относится к
Не II, правая (температура выше Т l) − к Не I.
К фазовым переходам 2-го рода относятся переходы магнетиков из ферромагнитного в парамагнитное состояние; диэлектриков из сегнето-электрического в «обычное» состояние; проводников из «нормального» в сверхпроводящее состояние. К этой же категории относится переход жидкого Не4 из «нормального» состояния Не I в сверхтекучее состояние Не II. Линия этого фазового перехода (T =2,18 К при ре=р 0)показана на рис. 1-6.
Сосуществующие в равновесии фазы при фазовом переходе 2-го рода отличаются не типом молекулярной структуры, как при переходах 1-го рода, а лишь характером ее упорядоченности, чем и объясняются соотношения (1-67). Теория фазовых переходов 2-го рода была предложена Л. Д. Ландау [14]. Отметим, что точки фазовых переходов 2-го рода часто называют l -точками вследствие специфической формы температурной зависимости с Р, (д v /дТ)р и аналогичных свойств вещества вблизи температуры перехода Т l (р). Такова, в частности, зависимость теплоемкости Не4 в окрестности температуры перехода Не I − Не II (рис. 1-7).
Термодинамическое поведение вещества в однофазных областях и в областях сосуществования фаз принято иллюстрировать разнообразными диаграммами состояния, которые обычно подробно изучаются в курсах технической термодинамики [3, 23] и используются для анализа всевозможных процессов и циклов как в области высоких, так и низких температур.
В криогенике наиболее часто применяют диаграммы в координатах Т, s; h, s; h, Т; они не имеют существенных отличий от тех, которые используются в теплотехнике. Некоторые из этих диаграмм имеют, однако, специфический вид в низкотемпературной области. В качестве примера на рис. 1-8 приведена Т, s -диаграмма Не4 в окрестности l -точки, отвечающая фазовой диаграмме рис. 1-6, а на рис. 1-9 − Т, s -диаграмма вещества, фазовая диаграмма которого анализировалась ранее (см. рис. 1-5).
ТЕРМОДИНАМИЧЕСКОЕ ПОДОБИЕ
Представим потенциальную энергию межмолекулярного взаимодействия Ф2(г) (см. § 1-3 и рис. 1-2) в виде
(1-68) где ф{г*) −безразмерный потенциал взаимодействия, зависящий от безразмерного расстояния между молекулами г*. Введем также безразмерные температуру Т*, плотность р* и давление р*:
(1-69)
45
Выразим теперь через безразмерные переменные (1-69) параметры газа, входящие в вириальное разложение давления (1-36):
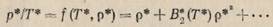(1-70)
Здесь 
−безразмерный второй вириальный коэффициент,
формула для вычисления которого следует из (1-37) и (1-68):
(1-71)
Как видно из (1-71), зависимость В\ от Т* и безразмерное уравнение состояния (1-70) одинаковы для разных газов, если у них совпадает безразмерный потенциал взаимодействия 
[15]. Сами же потенциалы взаимодействия Фг(г), точнее, их параметры еио могут при этом как угодно отличаться. Этот результат известен как закон соответственных состояний [под соответственными подразумеваются состояния разных веществ, в которых одинаковы безразмерные термодинамические переменные (1-69)], а вещества, у которых одинаково безразмерное уравнение состояния, называются термодинамически подобными.
Поскольку критические точки подобных веществ обязательно являются их соответственным состоянием, то вместо безразмерных параметров (1-69) на практике обычно пользуются приведенными параметрами:
(1-72)
так что приведенное уравнение состояния, одинаковое для всех подобных веществ, имеет вид:
(1-73)
Его определяют по экспериментальным данным о термодинамических свойствах детально изученных веществ. Тогда для расчета свойств какого-либо малоизученного вещества достаточно располагать лишь его критическими параметрами Т к, р к, v к:
(1-74)
Хорошо известно, что если бы вещества описывались уравнением Ван-дер-Ваальса (1-50), то приведенное уравнение состояния всех таких веществ 
было бы одинаковым [3]:
В действительности не все реальные вещества термодинамически подобны друг другу: подобие имеет место лишь для веществ, межмолекулярное взаимодействие в которых однотипно, − это и является причиной совпадения безразмерных потенциалов ф (r *). В частности, с достаточной точностью подобны друг другу вещества, состоящие из «сферически-симметричных» молекул, − инертные газы Аг, Кг, Хе, метан СН4, шестифтористая сера SF6 и т. д., а вещества, состоящие из полярных молекул, − водяной пар, аммиак, не могут описываться тем же самым приведенным уравнением состояния, поскольку механизм межмолекулярного взаимодействия у них существенно иной.
Чтобы включить в единый закон соответственных состояний более широкий круг веществ, вместо (1-73) используют [21] приведенное уравнение состояния в форме
(1-75) где 
Р\ и /*2 − функции, одинаковые для всех веществ, а параметр а, учитывающий тип межмолекулярного взаимодействия, одинаков для веществ, термодинамически подобных друг другу. В качестве такового можно использовать сжимаемость в критической точке 2к=РкУк/КТн или фактор Питцера [21].
Вещества, на поведение которых при низких температурах оказывают существенное влияние квантовые эффекты (гелий, неон, водород и его изотопы), отклоняются от закона соответственных состояний: для их подобия помимо совпадения безразмерных потенциалов ф (r *)требуется еще и равенство параметров де Бура 
где 
− постоянная Планка, а т − масса молекулы [15]. Поэтому, в частности, в этой области температур свойства изотопов водорода Н2, НD, D 2 и т. д. заметно отличаются, хотя с точки зрения классической физики можно было бы ожидать, что их уравнения состояния окажутся вообще идентичными.
