Расчет неармированных конструкций

Тема 17. РАСЧЕТ ЭЛЕМЕНТОВ КАМЕННЫХ КОНСТРУКЦИЙ

 

Предельные состояния и особенности расчета

 

● Расчет каменных и армокаменных конструкций ведут по методу предельных состояний. При этом учитывают две группы предельных состояний: первая — по несущей способности (прочности и устойчивости), вторая — по образованию и раскрытию трещин и по деформациям. Расчет по первой группе выполняют всегда и для всех видов конструкций. Расчет по второй группе выполняют для конструкций, где не допускаются трещины (облицовка резервуаров) или требуется ограничение их раскрытия (внецентренно сжатые элементы с большими эксцентриситетами), ограничиваются деформации по условиям совместной работы смежных конструкций (стеновые заполнения каркасов зданий) и др. Целью расчета являются подбор сечений элементов конструкций или проверка имеющихся сечений. Вычисленные напряжения, деформации и ширина раскрытия трещин не должны превышать предельных значений, установленных в [5]. Расчет по несущей способности производят из условия, что расчетное усилие F меньше или равно расчетной несущей способности элемента F_u. Расчетное усилие вычисляют при действии нагрузок, взятых с коэффициентом надежности по нагрузке γ_f (см. гл. 2) при неблагоприятном их сочетании. Расчетную несущую способность определяют в зависимости от геометрических размеров сечения, расчетного сопротивления кладки R и коэффициентов условий работы. Расчетное сопротивление, учитывающее возможность снижения прочности, связанное с естественным разбросом механических свойств, учитывается коэффициентом надежности γ и определяется по формуле R=R_u/γ, где R_u — временное сопротивление кладки; γ — принимается для всех видов кладок, работающих на сжатие, равным 2, на растяжение — 2,25. Другие обстоятельства, влияющие на несущую способность и деформативность, учитываются коэффициентом условий работы γ_с, на который умножается величина R. Например, при расчете прочности каменных и армокаменных конструкций площадью сечения 0,3 м² и менее расчетное сопротивление умножается на γ_c = 0,8.

 

 

Расчет неармированных конструкций

 

■ Расчет прочности центрально-сжатых элементов.

Расчет неармированных центрально-сжатых элементов по несущей способности производят в предположении равномерного распределения напряжений по сечению по формуле (рис. 17.1, а)

где N — расчетная продольная сила; m_g — коэффициент снижении несущей способности вследствие ползучести кладки, определяемый по формуле (17.3) при e_0g=0; φ — коэффициент, учитывающий снижение несущей способности элемента за счет продольного изгиба, зависящий от гибкости элемента λ и упругой характеристики кладки α; R — расчетное сопротивление кладки сжатию; А — площадь поперечного сечения элемента.

●Гибкость элемента любой формы представляет собой отношение расчетной длины к радиусу инерции сечения λ_i = l₀/i, а прямоугольного сечения λ_h = l₀/h, где h — наименьший размер сечения.

В элементах, имеющих неподвижные горизонтальные опоры (в стенах и столбах многоэтажных зданий), расчетная длина l₀ равна их фактической длине — высоте этажа H; в элементах, имеющих упругую верхнюю опору (стенах и столбах одноэтажных промзданий), l₀=1,25 Н для многопролетных зданий; l₀=1,5 H для однопролетных зданий; l₀=2Н в свободно стоящих стенах и столбах.

Рис. 17.1. К расчету элемента на центральное и внецентренное сжатие

 

Значение коэффициентов φ и m_g для стен и столбов, опирающихся на неподвижные шарнирные опоры, при расчете сечений, расположенных в средней трети высоты l₀, принимают постоянными и равными их значениям, определенным для данного элемента. При расчете сечений на участках в крайних третях l₀ коэффициенты φ и m_g увеличиваются по линейному закону до единицы на опоре. При других условиях защемления концов элемента φ и m_g определяют согласно [5].

Подбор сечений сжатых элементов производят путем последовательных приближений. Задавшись маркой и видом камня и раствора, находят по нормам расчетные сопротивления кладки сжатию. Приняв m_g = 1 и φ=0,9, по формуле (17.1) вычисляют размеры столба или стены. По найденным размерам определяют гибкость элемента, уточняют по [5] значения m_g и φ и производят повторный расчет.

■ Расчет прочности внецентренно сжатых элементов.

На внецентренное сжатие работают конструкции каменных зданий, в которых продольная сжимающая сила N приложена с эксцентриситетом. Если в сечении одновременно действует центрально-приложенная сила N и изгибающий момент М, то, как уже отмечалось (см. гл. 5), это эквивалентно одной силе N, приложенной с эксцентриситетом относительно центра тяжести сечения е₀ = M/N. Характер напряженного состояния каменной кладки в основном зависит от величины эксцентриситета продольной силы е₀.

При небольших эксцентриситетах все сечение сжато, эпюра напряжений имеет криволинейное очертание (рис. 17.1, б). По мере увеличения эксцентриситета сжимающие напряжения со стороны, удаленной от силы, уменьшаются, а затем меняют знак, т. е. возникает растяжение (рис. 17.1, в). Когда растягивающие напряжения превысят прочность шва на растяжение, образуется трещина, распространяющаяся на некоторую глубину t (рис. 17.1, г). После образования трещины продолжает работать под нагрузкой только часть сечения высотой h—t. Эксцентриситет приложения продольной силы N для этой части сечения оказывается уменьшенным (на величину t/2), т. е. сечение работает в условиях, приближающихся к центральному сжатию. Поскольку сжимающие напряжения распределены по сечению неравномерно, временное сопротивление кладки сжатию достигается первоначально в краевых участках. Однако при этом несущая способность не исчерпывается, так как в наиболее нагруженных участках вследствие ползучести развиваются значительные деформации, и тогда включаются в работу менее загруженные участки, которые сдерживают поперечные деформации сжатой зоны и тем самым повышают ее временное сопротивление по сравнению с временным сопротивлением при центральном сжатии. Это явление учитывается при расчете коэффициентом со, величина которого для кирпичной кладки прямоугольного сечения находится из выражения ω = 1+е₀/h≤1,45; при е₀=0 (центральное сжатие) ω=1.

Вследствие сложности напряженного состояния внецентренно сжатых элементов при расчете их прочности исходят из эмпирических формул, основанных на следующих допущениях: растянутая зона, если она имеется, исключается из работы; напряжения в сжатой зоне считаются распределенными равномерно (рис. 17.1, д); неравномерность распределения напряжений по сечению учитывается коэффициентом ω≥l.

Согласно нормам расчет внецентренно сжатых элементов производится по формуле

где m_g — коэффициент, учитывающий снижение несущей способности элемента при длительном действии нагрузки вследствие ползучести; φ₁ - коэффициент продольного изгиба; А_с — площадь сжатой части сечения при прямоугольной эпюре напряжений (рис. 17.1, д).

 

Коэффициент

где η — коэффициент, принимаемый по нормам в зависимости от гибкости элемента и вида кладки; для кладки из керамического кирпича при λ≤10 η = 0; N_g — расчетная продольная сила от длительных нагрузок; e_og — эксцентриситет от действия длительных нагрузок.

Коэффициент продольного изгиба φ₁ определяют как среднее арифметическое между коэффициентом продольного изгиба φ для всего сечения высотой h и коэффициентом продольного изгиба для сжатой части сечения элемента, высота которой для прямоугольного сечения h_c = h—2е₀. При расчете несущих и самонесущих стен толщиной 25 см и менее следует учитывать случайный эксцентриситет e_v, который должен суммироваться с эксцентриситетом продольной силы. Величину случайного эксцентриситета следует принимать: для несущих стен 2 см, для самонесущих 1 см.

Площадь сжатой части сечения А_с определяют из условия, что ее центр тяжести совпадает с точкой приложения расчетной продольной силы N.

В этом случае для прямоугольного сечения размер сжатой зоны будет h_c = 2 (h/2 — е₀), тогда А_с = h_cb = 2 (h/2—e₀)b=A(l—2e₀/h); при е₀=0 А_c=А.

Опыты показывают, что в элементах таврового сечения при эксцентриситетах е₀≤0,7y (рис. 17.1, е) (или прямоугольного сечения при е₀≤0,35h) может быть допущено небольшое раскрытие трещин в горизонтальных швах. Такое раскрытие не вызывает появления видимых трещин в облицовке и штукатурке стен. Однако при е₀>0,7у раскрытие швов становится заметным. Через образовавшиеся трещины в стену может проникать влага, вызывающая ее разрушение. В этом случае помимо расчета прочности необходим расчет кладки по раскрытию трещин.

Следует отметить, что во внецентренно сжатых конструкциях без продольного армирования в растянутой зоне наибольшая величина эксцентриситета (с учетом случайного) не должна превышать для основных сочетаний нагрузок 0,9у, для особых сочетаний — 0,95у, а при стенах толщиной 25 см и менее соответственно 0,8у и 0,85у. При этом расстояние от линии действия силы до более сжатого края сечения для несущих стен и столбов должно быть не менее 2 см.

■ Расчет на местное сжатие (смятие). Местное сжатие или смятие возникает в кладке при действии нагрузки на ограниченную область, т. е. только на часть сечения (рис. 17.2). В этом случае ненагруженная или менее нагруженная часть оказывает сопротивление поперечным деформациям, что приводит к повышению предела прочности кладки, подвергнутой местному сжатию.

Несущая способность сечения при местном сжатии

N_c≤ψdR_cA_c,                                         (17.4)

где N_c — величина местной нагрузки; ψ — коэффициент полноты эпюры давления от местной нагрузки: при равномерном распределении ψ=1, при треугольной эпюре давления ψ=0,5; d — коэффициент, учитывающий пластическую работу материала, для кирпичной и виброкирпичной кладки d = 1,5—0,5ψ; R_c = ξR — расчетное сопротивление кладки при местном смятии; А_с — площадь смятия, на которую непосредственно передается нагрузка.

Рис. 17.2. К определению расчетных площадей при местном смятии

 

Расчетное сопротивление кладки при местном смятии

R_c = ξR,

где ξ= ≤ξ₁; R — расчетное сопротивление кладки сжатию; А — расчетная площадь сечения кладки, включая площадь смятия и площадь соседних участков, установленную нормами [5]; ξ₁ — коэффициент, учитывающий максимально допустимое увеличение R_c по отношению к R; в зависимости от вида кладки и схемы расположения площади смятия ξ₁ = 1...2.

Если под опорами изгибаемых элементов не требуется установка распределительных плит, то для кладок из кирпича и бетонных камней допускается принимать ψd=1.

■ Расчет прочности изгибаемых элементов. Проектирование неармированных конструкций, работающих на изгиб, допускается только для кладок, работающих по перевязанному сечению. К таким конструкциям относятся подпорные стенки с вертикальными контрфорсами, стены здания между колоннами и т. п. Расчет сечений производят на действие изгибающего момента М и поперечной силы Q. При этом кладку условно рассматривают как упругий материал. Тогда по аналогии с известными положениями сопротивления материалов расчетные формулы примут вид:

■ при действии изгибающего момента

где R_tb — расчетное сопротивление кладки растяжению по перевязанному шву; W — момент сопротивления кладки при упругой ее работе;

●при действии поперечной силы

где R_tw — расчетное сопротивление кладки главным растягивающим напряжениям при изгибе, численно равное R_tb; b — ширина сечения; z — плечо внутренней пары, для прямоугольного сечения z=2h/3.

■ Расчет по образованию и раскрытию трещин. Расчет внецентренно сжатых неармированных элементов при е₀>0,7у помимо прочности производят по образованию и раскрытию трещин.

При расчете по раскрытию трещин (швов кладки) определяют краевые напряжения в сечении по неперевязанному шву в предположении упругой работы кладки, которые в целях ограничения ширины раскрытия трещин не должны превышать расчетного сопротивления кладки по неперевязанному сечению R_tb, умноженному на коэффициент условий работы γ_r:

где N — расчетная продольная сила; W — момент сопротивления сечения.

Коэффициент γ_r зависит от предполагаемого срока службы конструкции, характеристики и условий работы кладки. Так, для неармированной кладки внецентренно нагруженных конструкций при сроке их службы до 50 лет γ_r=2, а для конструкций при том же сроке службы, но испытывающих гидростатическое давление жидкости и снабженных гидроизоляцией, γ_r =1,5.

Полагая, что в выражении (17.7) M=Ne₀, и производя преобразования, получают

где I—момент инерции сечения; (h—у) — расстояние от центра тяжести сечения до наиболее удаленной растянутой грани.

Конструкции, в которых по условию эксплуатации не может быть допущено появление трещин в штукатурных и других покрытиях, должны быть проверены по допустимым деформациям растянутых поверхностей. Эти деформации для неармированной кладки следует определять при нормативных нагрузках, которые будут приложены после нанесения штукатурки или других покрытий. Расчет по деформациям растянутых поверхностей каменных конструкций из неармированной кладки производится по формулам:

●при осевом растяжении

●при внецентренном сжатии

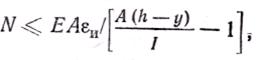
где Е — модуль деформаций кладки Е=0,8Е₀; е_u — предельная деформация кладки, при которой еще не происходит появление трещин; назначается в зависимости от вида штукатурки.

 

Армокаменные конструкции

 

Для повышения несущей способности каменные конструкции армируют: поперечной арматурой в виде сеток, укладываемых в горизонтальных швах кладки (рис. 16.1, а); продольной арматурой, устанавливаемой внутри кладки (рис. 16.1, б) или с внешней стороны в слое раствора и соединенной поперечными хомутами (рис. 16.1, г).

■ Сетчатое армирование (рис. 17.3). Это армирование получило наибольшее распространение, так как престо в производстве работ и эффективно применяется в кирпичных столбах и простенках малой гибкости l₀/h≤15 при небольших эксцентриситетах е₀≤0,17h. Усиление каменных сжатых элементов поперечным армированием происходит благодаря тому, что арматурные стержни, работая на растяжение, препятствуют расширению кладки в поперечном направлении, повышая ее несущую способность. Опыты показывают, что в центрально-сжатой кладке сетчатое армирование значительно эффективнее, чем продольная арматура, взятая в том же количестве.

Рис. 17.3. Косвенное армирование каменной кладки:

а — прямоугольными сетками; б — сетками «зигзаг»

 

Поперечную арматуру применяют в виде прямоугольных сеток (рис. 17.3, а) и сеток типа «зигзаг» (рис. 17.3, б) из сталей классов A-I и Вр-I. Прямоугольные сетки требуют для своей укладки большой толщины шва и применяются при диаметре проволоки 3...6 мм. Сетки «зигзаг» укладывают в двух смежных горизонтальных швах так, чтобы направление стержней в них было взаимно перпендикулярным. Две такие сетки равноценны одной прямоугольной, наибольший диаметр проволоки в них 8 мм. Расстояние между стержнями (с₁, с₂) должно быть не более 12 см и не менее 3 см. С увеличением расстояния между сетками по высоте кладки s эффективность их работы падает, поэтому сетки укладывают не реже чем через 5 рядов кладки из обыкновенного кирпича или 40 см для других видов камней. Степень насыщения кладки сетчатой арматурой характеризуется процентом μ армирования кладки по объему. Для сеток с квадратными ячейками для арматуры сечением A_st с размером ячейки с

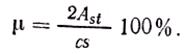
Минимальный процент армирования μ=0,1%, максимальный μ = 1,0%. Марка раствора для армокаменных конструкций должна быть не ниже 50.

Расчет элементов с поперечным армированием при центральном сжатии производят аналогично расчету неармированых элементов по формуле

где N — расчетная продольная сила; m_g — коэффициент снижения несущей способности вследствие ползучести (17.3); φ — коэффициент продольного, изгиба, определяемый в зависимости от приведенной гибкости и упругой характеристики кладки с сетчатым армированием [5]; R_sk — расчетное сопротивление при центральном сжатии для армированной кладки из кирпича при растворе марки 25 и выше

а для кладки на растворах марки ниже 25

 

где R₁ — расчетное сопротивление сжатию неармированной кладки в рассматриваемый срок твердения раствора; R_s — расчетное сопротивление арматуры, определяемое согласно [1] с учетом коэффициента условий работы γ_cs; для арматуры класса A-I γ_cs = 0,75, для Вр-I γ_cs=0,6; R₂₅ — расчетное сопротивление кладки при марке раствора 25.

■ Продольное армирование. Цель продольного армирования каменных конструкций (см. рис. 16.1, б) — повысить сопротивляемость кладки растягивающим усилиям и обеспечить монолитность и устойчивость отдельных конструкций и всего сооружения в целом. Продольная арматура может быть установлена внутри кладки или снаружи, в пазах или на поверхности в слое раствора (см. рис. 16.1, г). Марку раствора в целях защиты арматуры применяют не ниже 50. Во всех случаях продольная арматура связывается с кладкой хомутами, расстояние между которыми в сжатых элементах при расположении арматуры снаружи кладки должно быть не более 15d, а при расположении арматуры внутри кладки — не более 20d. Для армирования кладки применяют арматурную сталь классов A-I...A-III и обыкновенную арматурную холоднотянутую проволоку класса Вр-I. Работа армокаменных конструкций с продольным армированием аналогична работе железобетонных конструкций такого же типа, поэтому расчет их производят по той же методике, что и железобетонных. Однако в отличие от последних в центрально-сжатых и изгибаемых элементах к моменту достижения в стали предела текучести сопротивление кладки используется лишь на 85%, после чего совместная работа арматуры и кладки нарушается и начинается разрушение элемента. В связи с этим сопротивление кладки вводят в расчет с коэффициентом работы, равным 0,85. Расчетная формула для центрально-сжатых элементов с продольным армированием имеет вид

В центрально-сжатых элементах продольная арматура применяется в виде исключения, выгоднее и проще увеличивать сечение неармированной кладки или армировать кладку сетками.

Наряду с армированием усиление кладки может выполняться с помощью железобетона (см. рис. 16.1, в). При возведении такой комплексной конструкции кладка служит опалубкой для бетона. Применяют бетон класса В7,5...В10, продольную арматуру классов А-II и A-III. Площадь сечения продольной арматуры должна быть не менее 0,2% и не более 1,5% площади сечения бетона. Расчет комплексных конструкций аналогичен расчету элементов с продольным армированием. Центрально-сжатые элементы комплексных конструкций рассчитываются по формуле

Комплексные конструкции ввиду их повышенной трудоемкости применяются редко, например при строительстве в сейсмических районах.

 

 

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ:

1. Какие напряжения испытывает камень в кладке при сжатии?

2. Расчетные предельные состояния кладки.

3. Расчет прочности центрально-сжатых элементов.

4. Работа кладки при внецентренном сжатии и ее расчет.

5. Как влияет длительность действия нагрузки на несущую способность сжатых элементов?

6. Расчет прочности кладки при местном сжатии.

7. Расчет кладки по образованию и раскрытию трещин.

8. Виды армокаменных конструкций.

9. Сетчатое армирование. Особенности работы кладки и ее расчет.

10. Расчет кладки с продольным армированием.

11. Особенности работы комплексных конструкций.