| № п/п | Измеряемые и расчетные величины | Опыты | |
| 1 | 2 | ||
| 1 | Диаметр отверстия d, см | ||
| 2 | Площадь отверстия ω, см2 | ||
| 3 | Коэффициент расхода μ * | ||
| 4 | Начальный напор Н 1, см | ||
| 5 | Конечный напор Н 2, см | ||
| 6 | Объем воды в мензурке W, см3 | ||
| 7 | Время истечения от Н 1до Н 2(замеренное) t оп, с | ||
| 8 | Время истечения от Н 1до Н 2, вычисленное по формуле t расч, с
 **
| ||
| 9 | Относительная ошибка
| ||
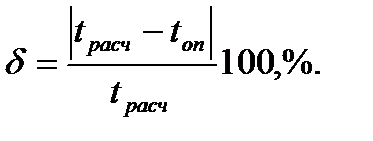
| Примечания: *Взять из работы 1.7 **При вычислении учесть, что g =981 см/с2 | |||
Часть 2. «ИССЛЕДОВАНИЕ ДИНАМИКИ ПОТОКОВ СЖИМАЕМОЙ ЖИДКОСТИ (ГАЗА)»
Лабораторная работа № 2.1
«Тарирование ротаметра»
Цель работы.
Тарирование (определение цены деления) ротаметра.
Общие теоретические сведения.
Расходом потока газа называется количество вещества, протекающее через живое сечение потока в единицу времени. Различают объемный Q [м3/с], и массовый G [кг/с] расходы.
Объемный расход потока Q в данном сечении равен произведению площади живого сечения на среднюю скорость потока
Массовый расход G определяется зависимостью
Взаимосвязь массового G и объемного Q расхода жидкости определяется формулой
Существует множество приборов различных типов для измерения расхода жидкости.
Измерение расхода сужающими устройствами.
В основе принципа действия этих устройств лежит закон сохранения энергии. Как было показано при изучении уравнения Бернулли, увеличение скорости приводит к снижению давления. Другой причиной падения давления могут быть потери напора при движении газа в канале или трубе. Чем выше скорость, тем эти изменения будут более значительными.
Сужающие устройства стандартизированы и имеют вполне определенную конструкцию, определенную требованиями нормативов. Схема сужающегося устройства представлена на рис. 2.1.1.
Как видно из рисунка, при прохождении отверстия диафрагмы происходит сужение живого сечения. Более того, за счет сил инерции жидкость еще некоторое время продолжает двигаться к центру. Таким образом, наибольшая скорость наблюдается на расстоянии D l от отверстия. Для измерения скорости необходимо иметь разность давлений между невозмущенным потоком в трубе перед диафрагмой и после. Именно для этого до- и после диафрагмы, подключается дифференциальный манометр (см. схему лабораторной установки).
Рис. 2.1.1. Схема сужающегося устройства (диафрагмы)
Зависимость между расходом и разностью давления устанавливается с помощью двух основных уравнений гидродинамики – Бернулли и уравнения сплошности
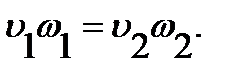
Потери напора происходят на относительно небольшом участке, в связи с чем учитываем только местные потери
С учетом этого, уравнение Бернулли примет вид
Как видно из рис. 2.1.1,а, центры живых сечений расположены на одинаковой высоте, в связи с чем, z 1 = z 2.
Разность давлений D р в сечениях измеряется специально устанавливаемым дифференциальным манометром.
С учетом сказанного, а также выразив скорость в первом сечении через скорость во втором сечении из уравнение сплошности
получим уравнение Бернулли в следующем виде
Т.к. в экспериментальной установке разность давлений представлена в виде разностей высот столба жидкости, а давление численно равно p = g h, получим
Выразим скорость из полученных уравнений
Введем величину, получившую название коэффициент сжатия струи
Учитывая, что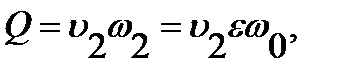 
получим зависимость для расхода
Безразмерный множитель получил название коэффициента расхода диафрагмы
Таким образом, для расхода получена формула
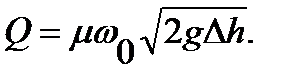
Коэффициент расхода зависит от диаметра отверстия, скорости течения и физических свойств газа. Физический смысл коэффициента расхода заключается в том, что он показывает во сколько раз расход через отверстие реального газа меньше, чем при истечении идеальногогаза. Поэтому в газе, не имеющем вязкости, а, следовательно, и потерь энергии (напора) на трение коэффициент расхода имеет значение μ=1.
Измерение расхода при помощи ротаметра.
Измерение расхода газа при помощи ротаметра основано на использовании силы динамического давления, действующей на тело, помещенное в поток. Сила динамического давления движущегося газа на тело, помещенное в этот поток, определяется по формуле
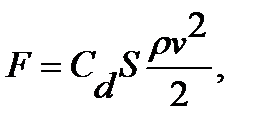
где С d коэффициент сопротивления трения; S –поперечная площадь обтекаемой поверхности.
Принципиальная схема ротаметра представлена на рис. 2.1.2.
Основные конструктивные элементы ротаметра: коническая, расширяющаяся вверх трубка, внутри которой снизу вверх пропускается воздух, расход которого мы измеряем; поплавок.
Рис. 2.1.2. Схема ротаметра
На поплавок действуют: сила тяжести, Архимедова сила, равная весу вытесненногогаза, а также сила динамического сопротивления. Из трех сил только сила динамического сопротивления зависит от скорости течения жидкости. Если поплавок неподвижен – силы уравновесили друг друга.
Как видно из формулы, сила динамического сопротивления пропорциональна квадрату скорости. Это значит, что даже небольшое изменение скорости приведет к ее существенному росту. Поплавок начнет перемещаться вверх. Так как трубка имеет форму конуса, расширяющегося вверх, подъем поплавка приведет к увеличению зазора между поплавком и трубкой, что, в свою очередь, приведет к снижению скорости движения потока (см. уравнение сплошности). Сила гидродинамического сопротивления также начнет уменьшаться. В какой то момент равновесие сил восстановится, а поплавок вновь остановится, но уже выше. Таким образом, по положению поплавка внутри трубки можно судить о величине расхода газа.
Экспериментальная установка.
Схема экспериментальной установки изображена на рис. 2.1.3.
Рис. 2.1.3.Схема лабораторной установки «Тарирование ротаметра».
Выполнение лабораторной работы.
Перед выполнением работы запишите диаметр отверстия диафрагмы. Измерив температуру в помещении, определите физические свойства газа, пользуясь справочными данными.
Включается насос и полностью открывается вентиль, регулирующий подачу газа (на выходе из насоса). Измеряются показания D Н дифференциального манометра. При помощи секундомера измеряют время t, за которое через расходомер пройдет 0,02 м3газа.
Полученные значения заносят в таблицу 2.1.1 отчета по лабораторной работе.
Прикрывая вентиль, уменьшают подачу газа. Замеры выполняют повторно и т.д. Замеров должно быть 5-6 до нулевой подачи включительно.
Таблица2.1.1
w0 = ___________ T = ____ 0C
| № | Опытные данные | Расчетные параметры | ||||||
| D Н, мм | V, м3 | t, сек | ν, м2/с | Q, м3/с | v, м/с | Re | m | |
| 1 | 0,02 | |||||||
| 2 | 0,02 | |||||||
| 3 | 0,02 | |||||||
| 4 | 0,02 | |||||||
| 5 | 0,02 | |||||||
| 6 | 0,02 | |||||||
Лабораторная работа № 2.2
«Исследование процесса истечения воздуха черезсуживающееся сопло»
Цель работы.
Экспериментальное изучение процесса адиабатного истечения воздуха через суживающееся сопло. Опытным путем определить зависимость скорости и расхода газа через суживающеесясопло и коэффициента истечения через него от величины перепада давлений на входе и выходе из сопла, характеризуемой отношением давлений р 2/ р 1.
Общие теоретические сведения.
Процессы течения газов по каналам осуществляются во многих машинах и аппаратах, поэтому изучение этих процессов и связанных с ними преобразований энергии в движущемся потоке газа имеетважное практическое значение. Основной задачей термодинамического анализа применительно к газовому потоку является определение скорости истечения, секундного расхода газа, а также установлениеусловий, существенно влияющих на процесс истечения и его эффективность.
При проведении исследований считаем, что течение газового потока установившееся и изоэнтропное.
При адиабатном установившемся течении газа увеличение кинетической энергии происходит засчет уменьшения его энтальпии, а, следовательно, и внутренней энергии. Увеличение скорости газа происходит при уменьшении его давления и температуры, а, следовательно, и при уменьшении местнойскорости звука. Теоретически массовый расход газа G т через сопло определится по выражению
(1)
где ω– площадь выходного сечения сопла, м2; k – показатель адиабаты для вытекающего газа; ρ1 – плотность газа на входе в сопло, кг/м3, ρ1=1/ v 1; v 1 – удельный объем газа на входе в сопло, м3/кг; р 1 и р 2 – абсолютные давления перед соплом и посленего, Па.
Выражение, находящееся под знаком корня, представляет собой удельный ток газа через сопло q тi– так называют массовый расход газа через единицу выходной площади, кг/(м2·с). В соответствии сзаконом сохранения массы, при установившемся течении величина массового расхода в любом i -м сечении сопла одна и та же: G i= G т= q тiωi= const.
Теоретическая скорость истечения из сопла для случая адиабатного истечения идеального газа при w 1=0 определяется формулой
(2)
Для водяного пара ее определяют через располагаемый теплоперепад
где h 1 и h 2 – энтальпии пара на входе в сопло и выходе из него. Конечно же, эта формула применима и для расчета скорости истечения газа, следует лишь рассчитать предварительно значения h 1 и h 2.
Если по формулам (1) и (2) рассчитать зависимость G т и w т от перепада давлений р 1– р 2, величинукоторого удобно характеризовать отношением давлений β= р 2/ р 1, то получим известные графики, приведенные на рис.2.2.1. Еще раз подчеркнем, что это чисто теоретические зависимости, поскольку помере увеличения перепада давлений (уменьшения отношения р 2/ р 1) скорость газа w увеличивается, достигает скорости звука а, и течение становится критическим. При этом дальнейшее увеличение перепададавлений уже не приводит к увеличению скорости газа на выходе из сопла.
Рис. 2.2.1.Графики зависимости w т=β(p 2/ p 1) и G т=β(p 2/ p 1) для воздуха
Преодолеть кризис течения и получить сверхзвуковые скорости газа, как известно, можно только спомощью сопла Лаваля, которое состоит из суживающейся части (конфузор), где скорость w может достичь скорости звука a, и расширяющейся части (диффузор), где происходит дальнейший разгон газа досверхзвуковой скорости w > a.
Известно, что критическое отношение давлений βкр, при котором скорость w достигает скоростизвука а, зависит от свойств газа и определяется соотношением
где k = c p/ c v– показатель адиабаты для данного газа. Для воздуха k =1,4 и βкр=0,528.
При критическом течении газа его теоретический расход G т и теоретическую скорость w т можнорассчитывать по тем же формулам (1) и (2), подставляя в них вместо отношения р 2/ р 1 значение βкр. Ряднесложных преобразований в этом случае позволяет несколько упростить названные формулы:
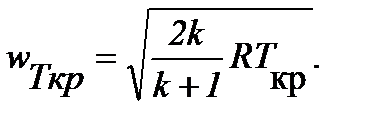
Здесь R = 287 Дж/(кг·К) – газовая постоянная сухого воздуха.
Для двухатомных газов (например, воздуха) k =1,4 и приведенные формулы можно записать так
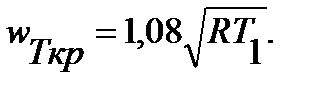
Следует заметить, что расчетные зависимости, приведенные на рис. 2.2.1, полученыдля равновесных адиабатных процессов, т.е. без учета потерь энергии газа на преодоление внутреннеготрения в системе.
В действительности процессы истечения через сопла и отверстия всегда неравновесные, необратимые.Они сопровождаются потерями работоспособности, увеличением энтропии и энтальпии газа и поэтому искорость w, и расход газа G всегда несколько ниже, чем теоретические w д< w т, G д< G т.
В расчетах это учитывают введением соответствующих коэффициентов
• коэффициент скорости φ= w д/ w т;
• коэффициент истечения μ= G д/ G т.
Значения этих коэффициентов находится опытным путем, и в этом состоит одна из целей работы. Обычно с увеличением скорости w д величины коэффициентов увеличиваются, а их численныезначения существенно зависят от ряда факторов, в том числе, от качества обработки поверхности канала, его формы и геометрических размеров.
Экспериментальная установка.
Схема экспериментальной установки изображена на рис. 2.2.2.
Рис. 2.2.2. Схема экспериментальной установки « Исследование процесса истечения воздуха черезсуживающееся сопло»
1 – ротаметр; 2 – счетчик газовый; 3 – диафрагма; 4, 8 – вентили регулировочные; 5, 7 – вакуумметры; 6 – сопло; 9 – ресивер; 10 – вакуум-насос; 11 – термометр; 12 – барометр: 13 – микроманометр
При включении вакуумного насоса 10, воздухоткачивается из ресивера 9, сглаживающего циклические колебания давления при работе насоса. Наружный воздух, засасываемый в ресивер, проходит предварительно через измерительные приборы (ротаметр 1, газовый счетчик 2 и диафрагму 3, подключенную к спиртовому микроманометру 13), иперетекает через суживающееся сопло 6 в ресивер 9. Вакуум перед соплом и после него измеряется техническими вакуумметрами 5 и 7 с трубкой Бурдона в качестве чувствительного элемента. Вентилями 4 и 8 можно изменять степень разряжения на входе и выходе исследуемого сопла, произвольно устанавливая различные перепады давления p 1– p 2 и, соответственно, разные отношения p 2/ p 1.
Выполнение лабораторной работы.
Перед началом экспериментов следует проверить, а при необходимости и поправить, «установкунуля» на микроманометре, убедившись, что спиртовые столбики в обоих капиллярах микроманометрарасполагаются против нулевого деления шкалы.
Экспериментальное исследование выполняется в две стадии. Сначала исследуют влияние изменения давления р 2 на расход газа при постоянстве давления р 1. Для этого перекрывают вентилем 8 выходиз ресивера, включают вакуум-насос и откачивают воздух из ресивера в течение 3-5 минут. После этого полностью открывают вентиль 8, выжидают 2-3 минуты для наступления установившегося режима(показания вакуумметра 7 перестанут изменяться), и записывают в таблицу исходных опытных данныхпоказания вакуумметров, ротаметра и микроманометра. Записывают показания газового счетчика, одновременно включая секундомер, и фиксируют продолжительность работы установки, пока через счетчик не пройдет ровно 10 литров воздуха. Продолжительность опыта тоже заносят в таблицу.
Далее, прикрывая вентиль 8, уменьшают проходное сечение для воздуха, тем самым уменьшая егорасход. В результате вакуум за соплом станет меньше (р 2вак≈0,6 кг/см2). Когда режим работы установится, записывают показания всех приборов и продолжительность перетекания 10 литров воздуха. Вентилем 8 еще раз уменьшают вакуум за соплом (р 2вак≈0,5 кг/см2) и проводят измерения. Аналогично проводят замеры при р 2вак≈0,4 кг/см2, р 2вак≈0,3 кг/см2, р 2вак≈0,2 кг/см2 и р 2вак≈0,1 кг/см2.
Другая серия опытов позволяет исследовать влияние изменения давления р 1 на расход воздуха. Дляэтого вновь полностью открывают вентиль 8, после чего прикрывают вентиль 4 так, чтобы вакуумметр 5 показывал разряжение р 1вак≈0,2 кг/см2. Дождавшись установившегося режима, опять записывают показания всех приборов и продолжительность перетекания 10 литров воздуха через газовый счетчик. Далее проводятся аналогичные опыты при р 1вак≈0,3 кг/см2, р 1вак≈0,4 кг/см2 и р 1вак≈0,5 кг/см2.
На основании калибровочных измерений заполняется таблица 2.2.1.
Таблица 2.2.1
Таблица исходных опытных данных*
| № п/п | р 1вак, кг/см2 | р 2вак, кг/см2 | z 1сч, см | z 2сч, см | N МК, мм | N рот, дел | τ, с |
| 1 | 0 | 0,56 | 1,614 | 1,624 | 214 | 96 | 131 |
| 2 | |||||||
| 3 |
* В качестве примера в таблице приведен один из результатов калибровочного опыта: барометрическое давление р к = 754 мм рт. ст. и температура t к = 18,9 oC.
По показаниям барометра и термометра фиксируем барометрическое давление и температуру в помещении (для всех опытов):
барометрическое давление р = _____ мм рт. ст.,
температура t = _____ oC.
Обработка опытных данных.
По результатам измерений для каждого из опытов находим:
1. Объемный расход при действительных параметрах воздуха р и t в помещении
2. Объемный расход, определенный по калибровочному графику микроманометра Q мкм и объемныйрасход по калибровочному графику ротаметра Q рот. Сопоставляем эти величины, делая заключение обих сравнительной точности.
3. Объемный расход, пересчитанный на параметры воздуха в помещении, отличающиеся от условий калибровки. Для этого запишем основное уравнение газовых состояний для условий калибровкии условий проведения наших опытов
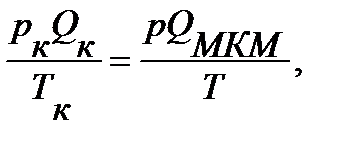
откуда находим
где Q к – объемный расход воздуха через сопло, отнесенный к егопараметрам, зафиксированным прикалибровке мерной шайбы, м3/с; р и р к – барометрическое давление во время опытов и во время калибровки, мм рт. ст.; Т и Т к – абсолютная температура воздуха во время опытов и во время калибровки, К.
4. Действительный массовый расход воздуха через сопло определяем из уравнения Клапейрона
или, по пересчитанному на условия калибровки расходу,
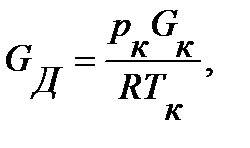
где R = 287 Дж/(кг·К) – газовая постоянная сухого воздуха.
5. Находим абсолютные давления р 1 и р 2, их отношение р 2/ р 1 и делаем заключение о характере течения (докритическое или критическое).
6. Рассчитываем теоретический массовый расход воздуха через сопло, учитывая, размер выходного сечение сопла будет определяться по формуле
7. Рассчитываем коэффициент истечения μ
μ= G д/ G т.
8. Рассчитываем теоретическую скорость истечения воздуха из сопла.
9. По действительному расходу газа G д рассчитываем действительную скорость истечения
где V 2д – удельный объем воздуха в выходном сечении сопла, определяемый давлением р 2 и температурой Т 2д газа в нем
Подчеркнем, что при критическом течении р 2= р 1βкр.
При отсутствии трения удельный объем V 2 и температура Т 2 на выходе из сопла легко рассчитываются по известным соотношениям:
и 
Ту же действительную скорость w 2д можно рассчитать и по другой формуле
где с р – средняя удельная теплоемкость воздуха при температуре 20-30оС. С высокой степенью точности с р=1003 Дж/(кг·К).
Приведенные формулыпредставляют собою систему из двух уравнений с двумя неизвестными w 2д и Т 2д,решать которую удобно методом последовательных приближений, задавая в качестве первого приближения значение Т 2д на 2-2,5 К больше, чем величина Т 2, рассчитанная по формуле
С такой температурой рассчитывают значения w 2д, целенаправленно подбирая величину Т 2д так, чтобы получаемые значения w 2д совпадали с точностью до2-3 %. Только тогда задача считается решенной.
10. Рассчитываем коэффициент скорости
11. Результаты расчетов для каждого из режимов заносятся в сводную таблицу 2.2.2.
Таблица 2.2.2
Сводная таблица результатов расчета *
| № п/п | p 1, МПа | p 2, МПа | p 2/ p 1 | Q, м3/с *105 | w Т, м/с | G Т, кг/с *105 | w 2д, м/с | G д, кг/с *105 | φ | μ |
| 1 | ||||||||||
| 2 | ||||||||||
| 3 |
* Для примера приведены результаты обработки одного из режимов.
12. Проводится оценка максимальных погрешностей определения коэффициентов μ и φ(как результатов косвенных измерений) для одного из режимов истечения.
13. Работа заканчивается анализом полученных зависимостей и формулированием выводов ирекомендаций.
14. На основании данных расчетов на рис. 2.2.3 строятся графики зависимости коэффициент скорости φикоэффициент расходаμ от отношения (p 2/ p 1), т. е. строятся графикиφ= f (p 2/ p 1)и μ= f (p 2/ p 1).
| φ, μ | |||||||||||||||||||
| β= р 2/ р 1 | |||||||||||||||||||
Рис. 2.2.3. Графики зависимости коэффициента скорости φ= f (p 2/ p 1)
икоэффициентарасходаμ= f (p 2/ p 1)
СПИСОК ЛИТЕРАТУРЫ
Основная литература:
1. Штеренлихт Д.Б. Гидравлика. Учебник. - М.: Колосс, 2009.
2. Кузьминский Р.А. Гидрогазодинамика. Учебное пособие. – М.: МИИТ, 2011.
Дополнительная литература:
3. Бекнев В.С. и др. Сборник задач и упражнений по газовой динамике. - М.: Машиностроение, 1992.
4. Альтшуль А. Д. Гидравлика и аэродинамика. - М.: Стройиздат, 1987.
5. Бондарев Е.Н. и др. Аэрогидродинамика. - М.: Машиностроение, 1993.
6. Давидсон В.Е. Основы газовой динамики в задачах. - М.: Высшая школа, 1987.
7. Самойлович Г.С. Гидрогазодинамика. - М.: Машиностроение, 1990.
8. Большаков В.А., Константинов Ю. М. и др. Справочник по гидравлике. - Киев: Вища школа, 1977.
9. Шевелев Ф.А., Шевелев А.Ф. Таблицы для гидравлического расчета водопроводных труб. Справочное пособие. - М.: Стройиздат,1987.
10. Журнал. Водоснабжение и санитарная техника.
