Методика ознакомления с геометрическими фигурами, их простейшими свойствами.
Основной задачей изучения геометрического материала в начальных классах является формирование у учащихся четких представлений и понятий о таких геометрических фигурах, как точка, прямая линия, отрезок прямой, ломаная линия, многоугольник, круг и т.д.
Одной из задач изучения геометрического материала является выработка у учащихся практических умений измерений и построения геометрических фигур с помощью чертежных и измерительных инструментов.
Ознакомление с геометрическими фигурами и их свойствами происходит постепенно на протяжении всех лет обучения в начальной школе.
С точкой учащиеся знакомятся с первых шагов обучения в 1-ом классе. Готовясь к письму цифр, дети по образцу учителя, ставят точки в середине клеточки, в нижнем углу клеточки, в середине одной из сторон клеточки и т.п.
После знакомства с линией и прямой линией, ставят точки на прямой, проводят прямые линии через одну, две точки. Определяют, какие точки принадлежат прямой, а какие - нет.
Таким образом, у учащихся накапливаются представления о том, что если прикоснуться карандашом (стержнем) к листу бумаги или мелом к доске, то получим точку.
В 3-ем классе (1 часть, с.14) учащиеся знакомятся с обозначением точек латинскими буквами.
Учитель сообщает, что точки на чертеже обозначаются заглавными большими буквами: A, B, C, D, E, K и др.
Чтобы назвать отрезок, обозначают точки, которые являются его концами. Например, отрезок ОМ. О ●---------------------------● М
В многоугольнике обозначают буквами его вершины. В С
Например, квадрат АВСD
А D
Дети упражняются в обозначении фигур буквами и чтении, обозначенных буквами, фигур.
В первом классе учащиеся знакомятся с прямой и кривой линией. При ознакомлении полезно использовать практический метод.
Например, натягивая нить (шнур, шпагат), дети подмечают, что получили прямую линию,
Ослабляя нить (шнур, шпагат) подмечают, что получили кривую линию.
Рассматривая рисунки на странице учебника, выясняют, какая получилась линия – прямая или кривая (Красная линия - прямая, так как шнур натянут, синяя линия - кривая, так как шнур провисает).
Затем учитель предлагает детям провести через точку а) кривые линии
б) прямые линии (с помощью линейки)
- Сколько прямых линий можно
● провести через одну точку?
● (множество).
Дети подмечают,
Что через точку можно
провести множество прямых.
На доступном уровне учитель знакомит учащихся с основным свойством прямой - ее бесконечностью.
Чтобы ученики смогли понять такое абстрактное понятие, как бесконечность прямой. Для этой же цели можно использовать длинную нить, натянутую на две катушки. (Нить яркая, толстая). Учитель вызывает двух учеников. Каждый из них берет катушку. Затем они расходятся в стороны на небольшое расстояние, туго натягивая нить.
– Какая получилась линия? (прямая)
– Можно ли ее продолжить и как? (Дети с катушками расходятся дальше до тех пор, пока не дойдут до стен класса).
Затем полезно выполнить такие задания, в процессе которых дети научились различать такие понятия, как «точка пересечения двух линий», «линия проходит через точку» и т. п.
На следующем этапе знакомятся с отрезком.
Ознакомление проводится практически: учитель чертит прямую, отмечает на ней две точки и поясняет, что часть прямой от одной точки до другой называют отрезком. Точки - называют концами отрезка.
● ●
Дети подмечают: у отрезка есть начало и конец.
Закреплению понятия об отрезке способствуют такие упражнения: показать отрезки прямой на окружающих предметах; соединить отрезком две точки; сравнить отрезки по длине и другие.
В дальнейшем после знакомства с единицами длины, учащиеся выполняют большое количество упражнений в измерении и черчении отрезков; решают задачи с отрезками (на увеличение и уменьшение на несколько единиц и в несколько раз, на разностное и кратное сравнение).
При работе с учебником (М - 1, с. 26) учитель знакомит учащихся с понятием "многоугольник" и частными видами многоугольников.
Ознакомить можно так:
 | |||||||
 |  | ||||||
 | |||||||
Учитель предлагает детям сравнить фигуры слева и справа.
– Что у них общего? (Они ограничены отрезками).
– Чем они отличаются? (Фигуры слева ограничены тремя отрезками, а фигуры справа - четырьмя отрезками).
– Как называются фигуры слева? (треугольники).
– Как называются фигуры справа? (четырехугольниками).
Учитель сообщает: фигуры, ограниченные отрезками, называются многоугольниками. Отрезки, которые ограничивают многоугольники, называются его сторонами.
– Сколько сторон у треугольника? (Три).
– Сколько сторон у четырехугольника? (Четыре).
Значит, мы можем сказать, что треугольник, это многоугольник, у которого три стороны.
– А как дать определение четырехугольника? (Четырехугольник, это многоугольник, у которого четыре стороны).
С целью закрепления дети находят среди фигур треугольники, четырехугольники, шестиугольники и другие, дают при этом соответствующее обоснование.
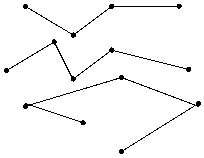
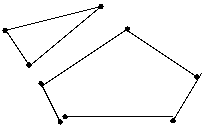
При работе по с. 35 (М - 1 1-4) знакомятся с ломаной линией и ее видами.
 | |||||
 | |||||
 | |||||
Что фигуры слева и справа состоят из отрезков, расположенных так, что конец одного является началом следующего отрезка и никакие два соседних отрезка не принадлежат одной прямой.
Учитель сообщает, что такие линии называются ломаными.
Отрезки, из которых состоят ломаные, называются звеньями.
– Чем ломаные справа отличаются от ломаных слева? (У ломаных слева - начало и конец не совпадают. У ломаных справа начало и конец совпадают).
Учитель сообщает: «Ломаные, у которых начало и конец не совпадают, называются не замкнутыми. Ломаные, у которых начало и конец совпадают, называются замкнутыми.»
Дети определяют количество звеньев в ломаной, определяют их вид.
Подмечают, что границей многоугольника является замкнутая ломаная линия.
Во 2-ом классе вводится понятие - длина ломаной линии.
На следующем этапе (2 класс) знакомятся с прямым углом.
При ознакомлении можно использовать практический метод:
Учитель предлагает детям лист бумаги произвольной формы дважды перегнуть пополам: «Мы получили модель прямого угла».
Разворачивая листы бумаги, дети подмечают, что линии сгиба (пересекающиеся прямые) образуют четыре прямых угла. Все прямые углы равны между собой.
Пользуясь моделью прямого угла, учащиеся находят прямые и не прямые углы на иллюстрациях учебника. В дальнейшем для установления вида угла используют прямой угол чертежного угольника.
Затем знакомятся с прямоугольником.
Учащиеся находят четырехугольники, у которых все углы прямые.
| |  |  | |||||||
 | |||||||||
 | |||||||||
И узнают, что четырехугольник, у которого все углы прямые, называется прямоугольником.
Выполняя упр. в учебнике узнают, что одинаковым цветом показаны противоположные стороны прямоугольника.
Дети перегибают пополам модели прямоугольников и подмечают, что противоположные стороны прямоугольника равны.
Затем из прямоугольников выделяют те, у которых все стороны равны.
Дают определение: Квадрат - это прямоугольник, у которого все стороны равны.
Для закрепления новых понятий выполняются задания: на распознавание геометрических фигур, на обобщение и классификацию фигур по различным признакам, на выделение данных фигур из сложного чертежа и другие.
В третьем классе знакомятся с периметром многоугольника.
Узнают, что периметр многоугольника - это сумма длин всех его сторон.
Измеряют стороны многоугольников и находят их периметр.
Для закрепления этого понятия выполняются задания, где используются свойства сторон прямоугольника для нахождения его периметра разными способами.
Стороны прямоугольника равны 3 см и 2 см. Объясни, почему его периметр можно найти так.
а) 2 · 2 + 3 · 2
б) Или так: (2 + 3) · 2
Ответ: 10 см
Объяснение: а) у прямоугольника противоположные стороны равны.
2 · 2 - это две ширины
3 · 2 - это две длины
2 · 2 + 3 · 2 - сумма всех сторон прямоугольника (т.е. периметр)
б) 2 + 3 - сумма ширины и длины.
Так как у прямоугольника 2-е суммы и 2-е ширины, то (2 + 3) · 2 - это сумма всех сторон, т.е. периметр прямоугольника.
Учащиеся находят периметр прямоугольника разными способами, а затем выбирают наиболее удобный.
Так как у квадрата все стороны равны, то чтобы найти периметр квадрата, надо его сторону умножить на 4.
На следующем этапе в третьем классе знакомятся с различными
видами треугольников в зависимости от длин сторон.
 |  | ||
1 2 3
Учащиеся измеряют длины сторон треугольника 1 и узнают: треугольники, у которых все стороны разной длины, называются разносторонними.
Затем измеряют стороны 2 и 3-го треугольников и узнают: треугольники, у которых две стороны равны, называются равнобедренными.
Треугольники, у которых все стороны равны, называют равносторонними.
В дальнейшем классифицируют треугольники в зависимости от длин сторон.
В четвертом классе учащиеся знакомятся с диагоналями прямоугольника и их свойствами.
В С Отрезки АС и ВD - диагонали прямоугольника.
Сравнивая по длине диагонали, приходят к выводу:
1) Диагонали прямоугольника равны
2) Отрезки, получаемые при пересечении
А D диагоналей прямоугольника, равные.
Диагонали квадрата обладают еще одним свойством:
При пересечении диагоналей квадрата всегда получаются прямые углы
На следующем этапе в 4 классе вводится определение угла и названия видов углов и классификация треугольников, в зависимости от видов углов.
 | |||
 | |||
М
1 А 2
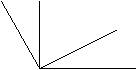
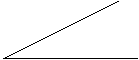
Фигура, образованная двумя лучами с одним и тем же началом, называется углом. Лучи, образующие угол – это стороны угла, а общее начало - вершина угла.
Угол может быть назван по его вершине: на чертеже 1 - это угол М, а на чертеже 2 изображено несколько углов с вершиной А. На чертеже 2 двумя красными лучами выделен прямой угол.
Угол, который меньше прямого, называют острым.
Угол, который больше прямого, называют тупым.
Учащиеся определяют виды углов на глаз и проверять при помощи угольника.
В зависимости от величины углов классифицируют треугольники на прямоугольные, остроугольные и тупоугольные
Треугольник, у которого все углы острые, называется остроугольным.
Треугольник, у которого есть прямой угол, называется прямоугольным.
Треугольник, у которого есть тупой угол, называется тупоугольным.
На следующем этапе знакомятся с окружностью и ее элементами.
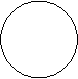А Граница круга - окружность
С D Точка О - центр окружности (круга)
В Отрезки, соединяющие центр окружности с любой ее точкой, - радиусы окружности.
В каждой окружности все радиусы равны.
Отрезок, соединяющий две точки окружности и проходящий через центр, - диаметр.
