Если непрерывная функция f (x) принимает на концах отрезка [ a, b ] значения разных знаков, то есть f (а)* f (b)<0, то внутри этого отрезка содержится, по крайней мере, один корень. Этот корень будет единственным, если производная f ¢ (x) существует и сохраняет постоянный знак внутри интервала (a, b).
Пример. Требуетсяотделить корни уравнения x 4 - x 3 - 2 x 2 +3 x – 3 = 0
Составим таблицу знаков функции f (x), полагая x равным:
a) критическим значениям функции (корням производной) или близким к ним;
b) граничным значениям (исходя из области допустимых значений неизвестного).
Вычислим: f ¢ (x) = 4 x 3 - 3 x 2 - 4 x + 3
Находим корни производной: x = -1, x = 1, x =3/4
В этих же точках, которые называются точками перегиба, функция имеет экстремумы.
Используя найденные значения корней, проверим значение функции в промежутках между ними.
| x | - ¥ | - 1 | 3/4 | 1 | + ¥ |
| знак f (x) | + | - | - | - | + |
Из таблицы видно, что функция меняет знак два раза, значит, уравнение имеет два действительных корня:
x 1 Î (- ¥, -1), x 2 Î (1, + ¥).
Уменьшим промежутки, в которых находятся корни:
| x | - 2 | - 1 | 1 | 2 |
| знак f (x) | + | - | - | + |
Следовательно, x 1 Î (- 2; -1), x 2 Î (1; 2).
Используя процедуру Поиск решения, найдем все корни уравнения x 4 - x 3 - 2 x 2 +3 x – 3= 0
Значение х запишем в ячейку А1, в ячейку В1 напишем формулу для вычисления f (x), выполним команду Сервис – Поиск решения, запишем в окне диалога ограничения на значения интервала решения.
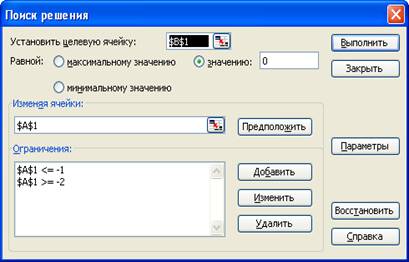
Нажав кнопку Выполнить, найдем значение первого корня.
Аналогично можно найти значение второго корня и три значения функции в точках экстремумов.
ЗАДАНИЕ:
Найти решение следующих пяти задач в табличном процессоре MS Excel согласно варианту. Решение, все его шаги и используемые формулы описать в пояснительной записке к каждой задаче домашнего задания (возможно принтование экранов Excel с решением и кратким пояснением в доступном для чтения масштабе).
ЗАДАЧА 1
1. Вычислить значения функции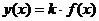 
для всех значений переменной х на отрезке [ a; b ] с шагом h при заданном значении k.
Решение должно быть получено в виде таблицы:
| № | x | k | f(x) | y(x) |
2. На основании данных таблицы построить совмещенные графики функций f (x) и y (x).
ВАРИАНТЫ
| № | a | b | h | k | f(x) |
| 1 | 1 | 1,5 | 0,05 | 5 | sin(x) - 1/x |
| 2 | -1 | 0 | 0,1 | 4 | cos(x) - 1/(x+2) |
| 3 | 1 | 1,2 | 0,02 | 3 | 4x2 - cos(x) – 4 |
| 4 | 0 | 1 | 0,1 | 2 | cos(x) + 1/(x-2) |
| 5 | -1 | 0 | 0,1 | 9 | ex + 2sin(x) |
| 6 | -1 | 0 | 0,1 | 7 | x + 1/(x2+1) |
| 7 | -1 | 0 | 0,1 | 8 | ex + x |
| 8 | -2 | -1 | 0,1 | 6 | cos(x)-1/(x-2) |
| 9 | 1 | 2 | 0,1 | 4 | e -x - ln(x) |
| 10 | 0 | 1 | 0,1 | 7 | e -x - x |
| 11 | 0 | 1 | 0,1 | 3 | cos(x) - x2 |
| 12 | -2 | 0 | 0,2 | 4 | x3 - x2 + 3 |
ЗАДАЧА 2
- Отделить корни алгебраического или трансцендентного уравнения f (x)=0, предварительно проанализировав область определения аргумента x.
- Используя процедуру Поиск решения найти:
все корни данного уравнения, все имеющиеся экстремумы (минимальные и максимальные значения) данной функции.
3. Построить график функции f (x) на конечном отрезке.
ВАРИАНТЫ
| № варианта | Уравнение f (x)=0 |
| 1 | x 3 - 3 x 2 - 4 x + 1=0 |
| 2 | x 3 – 21 x + 7=0 |
| 3 | 10 x = e - x |
| 4 | 2 x 3 + 2 x -1=0 |
| 5 | x 3 - 3 x – 1=0 |
| 6 | x3 - 3x2 +1 = 0 |
| 7 | x3 +6x2 + 9x+ 1= 0 |
| 8 | e-x = 2 – x2 |
| 9 | x3 - 12x + 5=0 |
| 10 | x3 - 2x +4=0 |
| 11 | x3 + x2 + 2 = 0 |
| 12 | x3 - x2 – 2 = 0 |
ЗАДАЧА 3
- Решить систему линейных алгебраических уравнений Ax = b с использованием математических функций для нахождения обратной матрицы A -1 и произведения матриц A -1 * b.
- Выполнить проверку найденного решения путем перемножения матриц A и x и сравнения полученного значения с b.
ВАРИАНТЫ
| № варианта | Матрица коэффициентов системы А | Столбец свободных членов b |
| 1 | 
| 
|
| 2 | 
| 
|
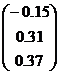
| 3 | 
| 
|
| 4 |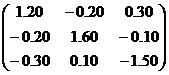 
| 
|
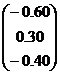
| 5 | 
| 
|
| 6 |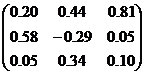 
| 
|
| 7 | 
| 
|
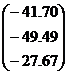
| 8 | 
| 
|
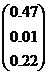
| 9 | 
| 
|
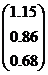
| 10 | 
| 
|
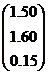
| 11 |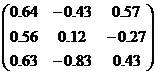 
| 
|
| 1 2 |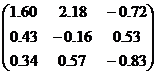 
| 
|
ЗАДАЧА 4
2. Расчет накопительного фонда для обучения производится по формуле:
S = V 0 · (1 + P) N , где V 0 - размер вклада (в рублях), который будет помещён в банк на определенный срок N (количество лет) под заданный процент P.
3. Вычислить:
