Одного уравнения движения (1.116) при математическом описании физического процесса недостаточно. Надо сформулировать условия, достаточные для однозначного определения процесса. При рассмотрении задачи о колебании струны дополнительные условия могут быть двух видов: начальные и граничные (краевые).
Сформулируем дополнительные условия для струны с закрепленными концами. Так как концы струны длины  закреплены, то их отклонения
закреплены, то их отклонения 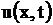 в точках
в точках  и
и  должны быть равны нулю при любых
должны быть равны нулю при любых  :
:
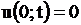 ,
, 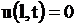
или
 , ,  . .
| (1.119) |
Условия (1.119) называются граничными условиями; они показывают, что происходит на концах струны на протяжении процесса колебания.
Очевидно, процесс колебаний будет зависеть от того, каким способом струна выводится из состояния равновесия. Удобнее считать, что струна начала колебаться в момент времени  . В начальный момент времени
. В начальный момент времени  всем точкам струны сообщаются некоторые смещения и скорости:
всем точкам струны сообщаются некоторые смещения и скорости:
 ,
, 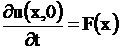
или
 , ,  , ,
| (1.120) |
где  и
и  - заданные функции.
- заданные функции.
Условия (1.120) называются начальными условиями.
Итак, физическая задача о колебаниях струны свелась к следующей математической задаче: найти такое решение уравнения (1.116) (или (1.117) или (1.118)), которое удовлетворяло бы граничным условиям (1.119) и начальным условиям (1.120). Эта задача называется смешанной краевой задачей, так как включает в себя и граничные и начальные условия. Доказано, что при некоторых ограничениях, наложенных на функции  и
и  , смешанная задача имеет единственное решение.
, смешанная задача имеет единственное решение.
Оказывается, что к задаче (1.116), (1.119), (1.120), помимо задачи о колебаниях струны, сводятся многие другие физические задачи: продольные колебания упругого стержня, крутильные колебания вала, колебания жидкостей и газа в трубе и др.
Помимо граничных условий (1.119) возможны граничные условия других типов. Наиболее распространенными являются следующие:
I.  ,
,  ;
;
II.  ,
,  ;
;
III.  ,
,  ,
,
где  ,
, 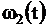 - известные функции, а
- известные функции, а  ,
,  - известные постоянные.
- известные постоянные.
Приведенные граничные условия называют соответственно граничными условиями первого, второго, третьего рода. Условия I имеют место в том случае, если концы объекта (струна, стержень и т.д.) перемещаются по заданному закону; условия II – в случае, если к концам приложены заданные силы; условия III – в случае упругого закрепления концов.
Если функции, заданные в правой части равенств, равны нулю, то граничные условия называются однородными. Так, граничные условия (1.119) – однородные.
Комбинируя различные перечисленные типы граничных условий, получим шесть типов простейших краевых задач.
Для уравнения (1.116) может быть поставлена и другая задача. Пусть струна достаточно длинная и нас интересует колебание ее точек, достаточно удаленных от концов, причем в течение малого промежутка времени. В этом случае режим на концах не будет оказывать существенного влияния и поэтому его не учитывают; струну же при этом считают бесконечной. Вместо полной задачи ставят предельную задачу с начальными условиями для неограниченной области: найти решение уравнения (1.116) для 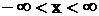 при
при  , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:
 ,
,  .
.
Эту задачу называют задачей Коши.
Если изучается процесс вблизи одной границы и влияние граничного режима на второй границе не имеет существенного значения на протяжении интересующего нас промежутка времени, то мы приходим к постановке задачи на полуограниченной прямой  . В этом случае задаются начальные условия и одно из граничных условий I-III при
. В этом случае задаются начальные условия и одно из граничных условий I-III при  .
.
К основным уравнениям математической физики относятся следующие уравнения в частных производных второго порядка.






