ВВЕДЕНИЕ В ТЕОРИЮ УРАВНЕНИЙ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Классификация дифференциальных уравнений
Многие задачи механики и физики могут быть сведены к дифференциальным уравнениям в частных производных. Математическими моделями реальных процессов являются краевые задачи для дифференциальных уравнений при определенных граничных и начальных условиях. При этом оказывается, что одно и то же уравнение может описывать совершенно различные по своей природе явления и процессы. Поэтому при исследовании довольно широкого круга задач механики и физики требуется сравнительно небольшое число различных видов дифференциальных уравнений. Изучением таких уравнений, методами их решения занимается раздел математики «Уравнения математической физики».
В нашем курсе мы будем заниматься уравнениями второго порядка. С помощью этих уравнений можно исследовать в первом приближении основные физические процессы: колебания, теплопроводность, диффузию, течение жидкостей и газа, электростатические явления.
Для решения своих проблем теория «Уравнений математической физики» использует различный математический аппарат: ряды Фурье, интегралы Фурье, интегральные преобразования (Лапласа, Фурье), функции комплексного переменного и др.
Специфическим для уравнений математической физики является то, что здесь постановка задач для уравнений в частных производных делается исходя из физических соображений. Процесс получения решения этих задач основывается на математических методах, но в каждом конкретном случае само решение той или иной задачи должно иметь определенную физическую интерпретацию.
Дифференциальные уравнения в частных производных.
Основные определения и понятия
Определение 1.40 Уравнение, связывающее неизвестную функцию нескольких переменных и ее частные производные, называется дифференциальным уравнением в частных производных.
Порядок высшей частной производной, входящей в уравнение, определяет порядок уравнения.
Для функции 
независимых переменных 
уравнение 
-го порядка имеет вид
 .
| (1.79) |
.
Обычно приходится иметь дело с уравнениями для функций двух, трех, четырех переменных.
Общий вид уравнений первого и второго порядков для функции 
двух переменных соответственно таков:
 ,
| (1.80) |
 ,
| (1.81) |
где
,,,,.
Решением уравнения в частных производных (1.79) называется всякая функция ( для уравнений (1.80), (1.81)), которая, будучи подставлена в уравнение вместо неизвестной функции и ее частных производных, обращает это уравнение в тождество по независимым переменным.
Познакомимся (без доказательства) с простейшими свойствами уравнений в частных производных на примерах некоторых их видов для функции двух переменных.
Рассмотрим для функции 
уравнение первого порядка вида
 .
| (1.82) |
Ясно, что искомая функция не зависит от переменной 
, но может быть любой функцией от 
:
 ,
| (1.83) |
поскольку, дифференцируя 
по 
, мы получим нуль, а это значит, что равенство (1.82) выполняется. Следовательно, решение (1.83) содержит одну произвольную функцию . В этом и заключается коренное отличие решения уравнения в частных производных первого порядка от общего решения обыкновенного дифференциального уравнения того же порядка, которое содержит лишь произвольную постоянную. По аналогии решение (1.83), содержащее одну произвольную функцию, будем называть общим решением уравнения (1.82).
Рассмотрим уравнение
 ,
| (1.84) |
где 
- заданная функция. Все функции , удовлетворяющие уравнению (1.84), имеют вид
 ,
| (1.85) |
где 
- произвольная функция от . Это можно проверить, дифференцируя обе части равенства (1.85) по . Найденное решение данного уравнения зависит от одной произвольной функции 
, т.е. является общим.
Рассмотрим теперь уравнение второго порядка
 .
| (1.86) |
Положим,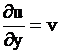 
, после чего уравнение (1.86) примет вид 
. Однако, как установлено, общее решение уравнения 
имеет вид (1.83), т.е. 
, где 
- произвольная функция. Исходное уравнение (1.86) перепишем так:
.
Согласно (1.85) его общим решением будет функция
.
Так как - произвольная функция, то интеграл от нее будет также произвольной функцией , которую обозначим через . В результате решение принимает вид
 ,
| (1.87) |
где , - произвольные дифференцируемые функции. Легко проверить, что функция вида (1.87) удовлетворяет уравнению (1.86).
Итак, решение (1.87) уравнения (1.86) второго порядка содержит уже две произвольные функции. Такое решение называется общим.
Приведенные уравнения дают основание сделать заключение: общее решение уравнения первого порядка в частных производных содержит одну произвольную функцию, а общее решение уравнения второго порядка – две произвольные функции.
Позже будет выяснено, какие дополнительные условия надо задать, чтобы с их помощью можно было выделить частное решение, т.е. функцию, удовлетворяющую как уравнению, так и дополнительным условиям.
Линейные дифференциальные уравнения
