Вопросы:
1.Постановка задачи аппроксимации функции одной переменной.
2. Метод наименьших квадратов.
3. Нахождение приближающей функции в виде основных элементарных функций
1.Постановка задачи аппроксимации функции одной переменной
Пусть в результате измерений в процессе опыта получено табличное задание некоторой функции f(х), выражающей связь между двумя переменными х и y:
| х | x1 | х2 | … | xn |
| f(x) | y1 | у2 | … | yn |
Конечно, можно найти формулу, выражающую эту зависимость аналитически, применив метод интерполяции (когда интерполирующая функция проходит через все заданные точки). Однако, совпадение значений полученного аналитического задания функции в узлах интерполяции с имеющимися эмпирическими данными часто может вовсе не означать совпадение характеров поведения исходной и интерполирующей функции на всем интервале наблюдения. Кроме того, табличная зависимость всегда получается в результате измерений различными приборами, имеющими определенную и не всегда достаточно малую погрешность измерения.
Требование точного совпадения значений приближающей и приближаемой функций в узлах является тем более неоправданным, если значения функции f(х), полученные в результате измерений уже сами являются приближенными или если х и y являются статистическими данными, что предполагает их вероятностный характер от выборки к выборке при неизменности тенденции.
Постановка задачи:
Формулировка задачи выглядит следующим образом:
Функция у= f(х) задана таблицей (1). Необходимо найти функцию заданного вида:
y=F(x) (2)
которая в точках x1, x2, …, xn принимает значения, как можно более близкие к табличным y1, y2, …, yn, при этом необязательно проходя через них.
Функция y=F(x) называется аппроксимирующей или приближающей функцией.
На практике вид приближающей функции чаще всего определяют путем сравнения вида приближенно построенного графика функции у=f(х) с графиками известных исследователю функций, заданных аналитически (чаще всего простых по виду элементарных функций). А именно, по таблице (1) строится точечный график f(x), затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек. По полученной таким образом кривой на качественном уровне устанавливается вид приближающей функции.

Рис. 1
На рисунке 1 изображены три ситуации:
· На графике (а) взаимосвязь х и у близка к линейной; прямая линия здесь близка к точкам наблюдений, и последние отклоняются от нее лишь в результате сравнительно небольших случайных воздействий.
· На графике (b) реальная взаимосвязь величин х и у описывается нелинейной функцией, и какую бы мы ни провели прямую линию, отклонение точек наблюдения от нее будет существенным и неслучайным. В то же время, проведенная ветка параболы достаточно хорошо отражает характер зависимости между величинами.
· На графике (с) явная взаимосвязь между переменными х и у отсутствует; какую бы мы ни выбрали формулу связи, результаты ее параметризации будут здесь неудачными. В частности, обе выбранные прямые одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной у по значениям переменной х.
Следует заметить, что строгая функциональная зависимость для таблицы исходных данных наблюдается редко, ибо каждая из участвующих в ней величин может зависеть от многих случайных факторов. Однако формула (2) (ее называют эмпирической формулой или уравнением регрессии у на х) интересна тем, что позволяет находить значения функции f для нетабличных значений х, "сглаживая" результаты измерений величины у, т.е. на всем интервале изменения х. Оправданность такого подхода определяется в конечном счете практической полезностью полученной формулы.
Вывод по первому вопросу: Необходимо найти аппроксимирующую функцию заданного вида y=F(x) (уравнение регрессии), которая в точках x1, x2, …, xn принимает значения, как можно более близкие к табличным y1, y2, …, yn, при этом необязательно проходя через них. Вид этой функции задается исследователем заранее.
2. Метод наименьших квадратов
Через имеющееся "облако" точек всегда можно попытаться провести линию установленного вида, которая является наилучшей в определенном смысле среди всех линий данного вида, то есть "ближайшей" к точкам наблюдений по их совокупности.
Для этого определим вначале понятие близости линии к некоторому множеству точек на плоскости. Меры такой близости могут быть различными. Однако, любая разумная мера должна быть, очевидно, связана с расстоянием от точек наблюдения до рассматриваемой аппроксимирующей линии (задаваемой уравнением y=F(x)).
Обозначим через Ui – отклонение, определяющее разность между заданной переменной yi и теоретической, рассчитанной по уравнению регрессии значений y i. (рисунок 2)
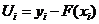
Очевидно, что чем меньше величина отклонения тем ближе точка находится к линии. Однако отклонение есть величина знаковая и при нахождении суммарной оценки отклонения могут компенсировать друг друга, давая в результате оценку, близкую к нулю. Для устранения знака каждое отклонение возводят в квадрат. Тогда в качестве критерия близости используется минимум суммы квадратов отклоненй i. Метод оценивания параметров приближающей функции, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции, называется методом наименьших квадратов (МНК) или Least Squares Method (LS).
 |
|
|
Рис.2
Вывод по второму вопросу: Задачу приближения функции f теперь можно сформулировать следующим образом: для функции f, заданной таблицей (1), найти функцию F определенного вида так, чтобы сумма квадратов отклонений была наименьшей.
 (3)
(3)
3. Нахождение приближающей функции в виде основных элементарных функций
Рассмотрим наиболее часто встречающиеся в практических исследованиях эмпирические зависимости.
3.1. Линейная функция (линейная регрессия).
Начальным пунктом анализа зависимостей обычно является оценка линейной зависимости переменных. Следует при этом учитывать, однако, что "наилучшая" по методу наименьших квадратов прямая линия всегда существует, но даже наилучшая не всегда является достаточно хорошей. Если в действительности зависимость y=f(x) является квадратичной, то ее не сможет адекватно описать никакая линейная функция, хотя среди всех таких функций обязательно найдется "наилучшая". Если величины х и у вообще не связаны, мы также всегда сможем найти "наилучшую" линейную функцию y=a0+а1х для данной совокупности наблюдений. Но в этом случае конкретные значения a0 и а1 определяются только случайными отклонениями переменных и сами будут очень сильно меняться для различных выборок из одной и той же генеральной совокупности.
Рассмотрим теперь задачу оценки коэффициентов линейной регрессии более формально. Предположим, что связь между x и y линейна и искомую приближающую функцию будем искать в виде:
 (4)
(4)
Тогда критерий близости по МНК будет иметь вид:
 (5)
(5)
Для минимизации данной функции найдем частные производные функции
2-х переменных и приравняем их к нулю:

 (6)
(6)
Получим систему 2-х уравнений с двумя неизвестными:
 (7)
(7)
После преобразования:
 (8)
(8)
Домножим первое уравнение на  , а второе на n и вычтем из второго первое уравнение:
, а второе на n и вычтем из второго первое уравнение:
 (9)
(9)
Пример: Пусть годовая производительность труда (в расчете на одного рабочего) и энерговооруженность на 14-ти предприятиях одной отрасли характеризуется данными:
 Предприятие
Предприятие
| Производительность труда, тыс.грн. на 1 рабочего (yi) | Энерговооруженность кВт на 1 рабочего (xi) | 
| 
|
| 1 | 6,7 | 2,8 | 7,84 | 18,76 |
| 2 | 6,9 | 2,8 | 7,84 | 19,32 |
| 3 | 7,2 | 3,0 | 9,00 | 21,60 |
| 4 | 7,3 | 2,9 | 8,41 | 21,17 |
| 5 | 8,4 | 3,4 | 11,56 | 28,56 |
| 6 | 8,8 | 3,9 | 15,21 | 34,32 |
| 7 | 9,1 | 4,0 | 16,00 | 36,4 |
| 8 | 9,8 | 4,8 | 23.04 | 47,04 |
| 9 | 10,6 | 4,9 | 24,01 | 51,94 |
| 10 | 10,7 | 5,2 | 27,04 | 55,64 |
| 11 | 11,1 | 5,4 | 29,16 | 59,94 |
| 12 | 11,8 | 5,5 | 30,25 | 64,9 |
| 13 | 12,1 | 6,2 | 38,44 | 75,02 |
| 14 | 12,4 | 7,0 | 49,00 | 86,8 |

| 132,9 | 61,8 | 296,8 | 621.41 |
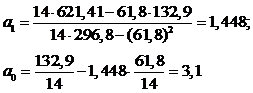
Тогда уравнение регрессии будет иметь вид:
 (10)
(10)
Необходимым условием для выбора линейной функции в качестве искомой эмпирической формулы является соотношение

Подсчитаем погршность:




Для оценки погрешности аппроксимирующей функции используем выражение:
 (11)
(11)
Тогда δ =






