1. Задача Коши для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами:
x (n) + a 1 x (n - 1) + a 2 x (n - 2) + … + an - 1 x ′ + anx = f (t),
x (0) = x 0, x ′ (0) = x 1, x ″ (0) = x 2, …, x (n -1) (0) = xn -1.
Начальные условия в этой задаче заданы в точке t 0 = 0. Если начальные условия задаются в другой точке t 0 ≠ 0, то заменой аргумента u = t - t 0 их сдвигают в точку u 0 = 0.
Метод решения этой задачи основан на теореме о дифференцировании оригинала. Предположим, что функция x (t), её производные до n -го порядка, правая часть f (t) являются функциями-оригиналами, и x (t)  X (p). Тогда x ′(t)
X (p). Тогда x ′(t)  p X (p) − x (0) = p X (p) − x 0, x ″(t)
p X (p) − x (0) = p X (p) − x 0, x ″(t)  p 2 X (p) − p x 0− x 1, …, x (n)(t)
p 2 X (p) − p x 0− x 1, …, x (n)(t)  p nX (p) − pn - 1 x 0 − pn - 2 x 1 − … − p x n - 2 − x n - 1, и изображение задачи будет иметь вид p nX (p) − pn - 1 x 0 − pn - 2 x 1 − … − p x n - 2 − x n - 1 + a 1(p n - 1 X (p) − pn - 2 x 0 − pn - 3 x 1 − … − x n - 2) + … + a n - 1(p X (p) − x 0) + a nX (p) = F (p), где F (p)
p nX (p) − pn - 1 x 0 − pn - 2 x 1 − … − p x n - 2 − x n - 1, и изображение задачи будет иметь вид p nX (p) − pn - 1 x 0 − pn - 2 x 1 − … − p x n - 2 − x n - 1 + a 1(p n - 1 X (p) − pn - 2 x 0 − pn - 3 x 1 − … − x n - 2) + … + a n - 1(p X (p) − x 0) + a nX (p) = F (p), где F (p)  f (t) - изображение правой части уравнения. Это линейное относительно X (p) алгебраическое уравнение, решив которое, находим X (p). Оригинал этого изображения и будет решением задачи Коши.
f (t) - изображение правой части уравнения. Это линейное относительно X (p) алгебраическое уравнение, решив которое, находим X (p). Оригинал этого изображения и будет решением задачи Коши.
Пример. Найти решение задачи Коши x ″ − 2 x ′ + x = e t, x (0) = 1, x ′(0) = 2.
Решение. Пусть x (t)  X (p). Тогда x ′(t)
X (p). Тогда x ′(t)  p X (p) − x (0) = p X (p) − 1, x ″(t)
p X (p) − x (0) = p X (p) − 1, x ″(t)  p 2 X (p) − p − 2,
p 2 X (p) − p − 2,  , и изображение задачи имеет вид
, и изображение задачи имеет вид  . Находим X (p):
. Находим X (p): 
 . Обращаем это изображение:
. Обращаем это изображение:  ,
,  . Решение задачи:
. Решение задачи:  .
.
2. Общее решение дифференциального уравнения с постоянными коэффициентами. Заметим, что решив задачу Коши с произвольными начальными условиями, мы получим общее решение уравнения. Так, для задачи предыдущего пункта x ″ − 2 x ′ + x = e t, x (0) = C 1, x ′(0) = C 2, изображение будет иметь вид 
 . Решение задачи зависит от двух произвольных постоянных, представляет собой сумму общего решения соответствующего однородного уравнения x общ. одн. = С 1 e t + (С 2 − С 1) t e t и частного решения
. Решение задачи зависит от двух произвольных постоянных, представляет собой сумму общего решения соответствующего однородного уравнения x общ. одн. = С 1 e t + (С 2 − С 1) t e t и частного решения  , следовательно, является общим решением уравнения.
, следовательно, является общим решением уравнения.
3. Краевая задача для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами. Если найдено общее решение уравнения, оно может быть использовано для решения краевой задачи. Пусть, например, задана краевая задача x ″ − 2 x ′ + x = e t, x (1) = x 1, x ′(3) = x 2, где x (1), x (2) - известные числа. Так как общее решение уже известно:  , остаётся найти значения произвольных постоянных, при которых выполняются краевые условия:
, остаётся найти значения произвольных постоянных, при которых выполняются краевые условия:  следовательно, решение краевой задачи равно
следовательно, решение краевой задачи равно

4. Уравнения с импульсной и составной правой частью. Это, возможно, единственный случай, когда операционное исчисление имеет преимущество перед другими методами решения рассматриваемых задач. Теорема запаздывания (20.2.4) позволяет полностью сохранить изложенный порядок действий. В качестве примера рассмотрим задачу x ″ − 2 x ′ + x = e t, x (0) = 1, x ′(0) = 2, где f (t) - изображённая на рисунке периодическая функция периода Т:
Изображение первого периода  мы нашли в 20.2.4.1:
мы нашли в 20.2.4.1:  ; изображение всей правой части, согласно разделу 20.2.4.3. Периодические функции, равно
; изображение всей правой части, согласно разделу 20.2.4.3. Периодические функции, равно  ; изображение уравнения
; изображение уравнения 
 . Оригиналы для первых двух слагаемых выписываются просто; для обращения последнего слагаемого представим произведение
. Оригиналы для первых двух слагаемых выписываются просто; для обращения последнего слагаемого представим произведение  в виде
в виде 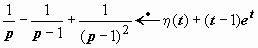 , множитель
, множитель  развернем в геометрическую прогрессию
развернем в геометрическую прогрессию  , тогда
, тогда  , следовательно,
, следовательно, 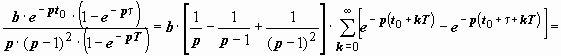
 . Оригинал для каждого слагаемого этой суммы обозначим f k (t), по теореме запаздывания
. Оригинал для каждого слагаемого этой суммы обозначим f k (t), по теореме запаздывания 
 ; так как
; так как  . Таким образом, решение всей задачи имеет вид
. Таким образом, решение всей задачи имеет вид  .
.
5. Формулы Дюамеля. При решении задачи Коши для обыкновенного дифференциального уравнения согласно тому порядку действий, который изложен выше, необходимо находить изображение правой части уравнения, что в некоторых случаях может быть затруднительно или вообще невозможно. Формулы Дюамеля позволяют находить решение, не выписывая в явной форме изображение правой части. Они основаны на интегралах Дюамеля,  ,
,
 .
.
Рассмотрим, наряду с полной задачей
x (n) + a 1 x (n - 1) + a 2 x (n - 2) + … + an - 1 x ′ + anx = f (t),
x (0) = x 0, x ′ (0) = x 1, x ″ (0) = x 2, …, x (n -1) (0) = xn -1,
для функции x (t) вспомогательную задачу для функции z (t):
z (n) + a 1 z (n - 1) + a 2 z (n - 2) + … + an - 1 z ′ + anz = 1,
z (0) = 0, z ′ (0) = 0, z ″ (0) = 0, …, z (n -1) (0) = 0.
Особенность этой вспомогательной задачи - простая правая часть (f (t) = 1) и однородные (нулевые) начальные условия. Её изображение имеет вид p nZ (p) + a 1 p n - 1 Z (p) + a 2 p n - 2 Z (p) + … + a n - 1 pZ (p) + a n Z (p) = 1/ p 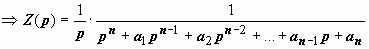 . Обратить это изображение можно любым методом: с помощью свёртки, по второй теореме разложения (все особые точки - полюса), или разложив дробь на простые слагаемые.
. Обратить это изображение можно любым методом: с помощью свёртки, по второй теореме разложения (все особые точки - полюса), или разложив дробь на простые слагаемые.
Рассмотрим ещё одну вспомогательную задачу для функции z 1(t):
z 1 (n) + a 1 z 1 (n - 1) + a 2 z 1 (n - 2) + … + an - 1 z 1 ′ + anz = 1,
z 1(0) = 0, z ′1 (0) = 0, z ″1 (0) = 0, …, z 1 (n -1) (0) = 0,
которая отличается от общей задачи однородными начальными условиями, а от первой вспомогательной задачи - общим видом правой части. Её изображение имеет вид p nZ 1(p) + a 1 p n - 1 Z 1(p) + a 2 p n - 2 Z 1(p) + … + a n - 1 pZ 1(p) + a n Z 1(p) = F (p) ⇒  .
.
Сравнивая функции Z (p) и Z 1(p), получаем Z 1(p) = pF (p) Z (p). В соответствии с интегралами Дюамеля,
 , или
, или 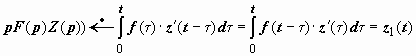 (так как z 1(0) = 0).
(так как z 1(0) = 0).
Эти формулы, выражающие решение задачи с произвольной функцией f (t) и однородными (нулевыми) начальными условиями через решение задачи с f (t) = 1 и такими же граничными условиями, называются формулами Дюамеля.
Наконец, чтобы учесть общий вид начальных условий, рассмотрим третью вспомогательную задачу (относительно функции y (t) - с нулевой правой частью:
y (n) + a 1 y (n - 1) + a 2 y (n - 2) + … + an - 1 y ′ + any = 0,
y (0) = x 0, y ′ (0) = x 1, y ″ (0) = x 2, …, y (n -1) (0) = xn -1, p nY (p) − pn - 1 x 0 − pn - 2 x 1 − … − p x n - 2 − x n - 1 + a 1(p n - 1 Y (p) − pn - 2 x 0 − pn - 3 x 1 − … − x n - 2) + … + a n - 1(p Y (p) − x 0) + a nY (p) = 0
 . Обращая это изображение, находим функцию Y (t) решение третьей задачи. Теперь решение x (t) полной задачи равно сумме полученного по одной из формул Дюамеля решения z 1(t) второй вспомогательной задачи (с общей правой частью и однородными (нулевыми) начальными условиями) и решения y (t) третьей вспомогательной задачи (с однородным уравнением и общими граничными условиями).
. Обращая это изображение, находим функцию Y (t) решение третьей задачи. Теперь решение x (t) полной задачи равно сумме полученного по одной из формул Дюамеля решения z 1(t) второй вспомогательной задачи (с общей правой частью и однородными (нулевыми) начальными условиями) и решения y (t) третьей вспомогательной задачи (с однородным уравнением и общими граничными условиями).
Пример. x ″ + x = tg t, x (0) = 1, x ′(0) = 2.
Решение. Функция tg t не является оригиналом (разрывы второго рода), поэтому найти её изображение невозможно. Решаем задачу с f (t) = 1и однородными начальными условиями:  , по формуле Дюамеля
, по формуле Дюамеля  находим решение задачи с f (t) = tg t и нулевыми начальными условиями:
находим решение задачи с f (t) = tg t и нулевыми начальными условиями: 

 .
.
Наконец, решаем однородное уравнение с заданными начальными условиями:  . Решение исходной задачи - сумма двух последних функций:
. Решение исходной задачи - сумма двух последних функций:  .
.
6. Решение систем линейных уравнений. Системы решаются так же, как и отдельные уравнения, поэтому сразу рассмотрим пример.
Найти решение системы  удовлетворяющее условиям: x (0) = 1, x ′(0) = 2, y (0) = 0, y ′(0) = 1 при t = 0.
удовлетворяющее условиям: x (0) = 1, x ′(0) = 2, y (0) = 0, y ′(0) = 1 при t = 0.
Решение. Пусть x (t)  X (p), y (t)
X (p), y (t)  Y (p). Тогда x ′(t)
Y (p). Тогда x ′(t)  p X (p) − 1, y ′(t)
p X (p) − 1, y ′(t)  p Y (p), x ″(t)
p Y (p), x ″(t)  p 2 X (p) − p − 2, y ″(t)
p 2 X (p) − p − 2, y ″(t)  p 2 Y (p) − 1, и изображение задачи имеет вид
p 2 Y (p) − 1, и изображение задачи имеет вид 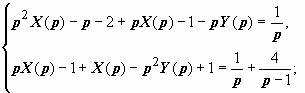

Решаем эту систему относительно X (p), Y (p): из первого уравнения вычитаем второе, умноженное на р:  (после разложения на простые дроби)
(после разложения на простые дроби)  ;
;
Если на р умножить первое уравнение и вычесть второе, получим 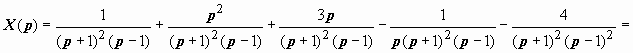
 . Итак, решение задачи
. Итак, решение задачи
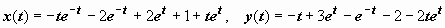 . .
|






