Коэффициент корреляции между случайными переменными X и Y определяется как
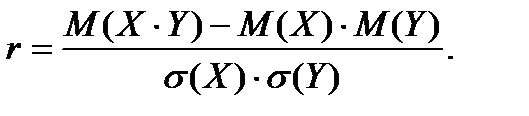
Его оценкой является выборочный коэффициент корреляции, который можно вычислить как:
 , где
, где
 – выборочное среднее произведение величин Х и Y,
– выборочное среднее произведение величин Х и Y,
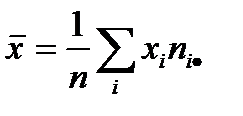 – выборочное среднее значение случайной величины Х,
– выборочное среднее значение случайной величины Х,
 – выборочное среднее значение случайной величины Y,
– выборочное среднее значение случайной величины Y,
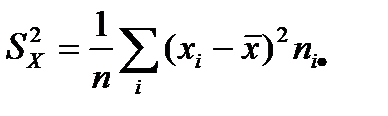 – выборочная дисперсия случайной величины Х,
– выборочная дисперсия случайной величины Х,
 – выборочная дисперсия случайной величины Y,
– выборочная дисперсия случайной величины Y,
Выборочный коэффициент корреляции обладает свойствами, аналогичными свойствам теоретического коэффициента корреляции:
1) Коэффициент корреляции принимает значения из промежутка [-1; 1]
 .
.
2) Если переменные Х и Y умножить на одно и то же число, то коэффициент корреляции не измениться.
3) Если  , то корреляционная связь между переменными представляет собой линейную зависимость.
, то корреляционная связь между переменными представляет собой линейную зависимость.
После вычисления выборочного коэффициента корреляции проверяют гипотезу о значимости связи, так как выборочный коэффициент корреляции, как правило, не совпадает с теоретическим коэффициентом корреляции и может не равняться нулю из–за отбора переменных в выборку.
Обычно проверяется основная гипотеза об отсутствии корреляционной связи.
Н0: r = 0 против альтернативы Н1: r ¹ 0.
В случае справедливости основной гипотезы Н0 статистика
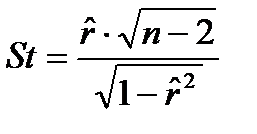
имеет распределение Стьюдента с n -2 степенями свободы.
Считают, что выборочный коэффициент корреляции значимо отличается от нуля, если значение статистики по модулю больше критического
 ,
,
где  - критическое значение распределения Стьюдента, определённое на уровне значимости a при числе степеней свободы, равном n -2 (т.е. квантиль уровня
- критическое значение распределения Стьюдента, определённое на уровне значимости a при числе степеней свободы, равном n -2 (т.е. квантиль уровня 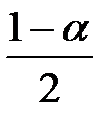 распределения Стьюдента с n -2 степенями свободы).
распределения Стьюдента с n -2 степенями свободы).
Введение в регрессионный анализ.
Первоначально термин «регрессия» был употреблён Ф. Гальтоном (1886) в теории наследственности в следующем специальном смысле. «Возвратом к среднему состоянию» (regression to mediocrity) было названо явление, состоящее в том, что дети тех родителей, рост которых превышает среднее значение на а единиц, имеют в среднем рост, превышающий среднее значение, меньше, чем на а единиц.
Регрессионная зависимость является частным случаем стохастической зависимости и подразумевает зависимость среднего значения величины Y от другой случайной величины Х (одномерной или многомерной).
Регрессионная зависимость Y от Х проявляется в изменении средних значений Y при изменении Х, хотя при каждом фиксированном значении Х=х величина Y остаётся случайной величиной с определённым распределением.
Регрессия случайной величины Y по Х – это условное математическое ожидание Y, вычисленное при условии, что случайная величина Х приняла значение, равное х:
y (x)= M (Y | X = x).
В математической статистике имеют дело с оценками соответствующих вероятностных характеристик, поэтому в качестве оценки условного математического ожидания принимают условное среднее. Если при каждом значении  наблюдается
наблюдается 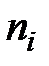 значений
значений  величины y, то зависимость средних арифметических
величины y, то зависимость средних арифметических

от  и является регрессией в статистическом понимании этого термина.
и является регрессией в статистическом понимании этого термина.
Если число наблюдений, соответствующее некоторым значения Х недостаточно велико, то такой метод может привести к ненадёжным результатам.
Уравнение y = y (x), в котором х играет роль «независимой» переменной, называют уравнением регрессии, а соответствующий график – линией или кривой регрессии.
Линия регрессии может быть приближенно восстановлена по достаточно обширной корреляционной таблице: за приближенное значение у(х) принимают среднее из тех наблюдённых значений Y, которым соответствует значение Х = х.
Для выяснения вопроса, насколько хорошо регрессия передаёт изменение Y при изменении Х, используется условная дисперсия Y при данном значении Х = х – дисперсия Y относительно линии регрессии (мера рассеяния относительно линии регрессии):
 .
.
При точной функциональной зависимости величина Y при данном Х=х принимает лишь одно определённое значение, то есть рассеяние вокруг линии регрессии равно нулю. Таким образом, если  при всех значения х, то можно с достоверностью утверждать, что Y и Х связаны строгой функциональной зависимостью. Если
при всех значения х, то можно с достоверностью утверждать, что Y и Х связаны строгой функциональной зависимостью. Если  ни при каком значении х и y (x) не зависит от x, то говорят, что регрессия Y по Х отсутствует.
ни при каком значении х и y (x) не зависит от x, то говорят, что регрессия Y по Х отсутствует.
Наиболее простым является тот случай, когда регрессия Y по Х линейна:
y = a ∙ x + b
(числа a и b называют коэффициентами регрессии).
Коэффициенты линейной регрессии вычисляют по формулам:
 ,
, 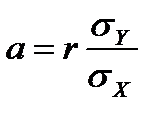 .
.
Здесь  ,
,  ,
,  ,
,  ,
,  .
.
Если двумерное распределение Y и Х нормально, то линия регрессии Y по Х (так же как и Х по Y) является прямой с уравнением
 .
.
В этом случае корреляционное отношение совпадает с коэффициентом корреляции и условная дисперсия не зависит от х (является постоянной величиной):
.
Следовательно, коэффициент корреляции полностью определяет степень концентрации распределения вблизи линии регрессии.
Если регрессия Y по Х отлична от линейной, то уравнение
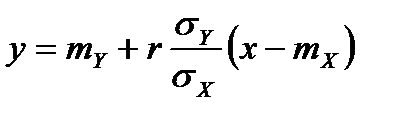 .
.
является линейным приближением истинного уравнения регрессии.
Коэффициенты регрессии обычно неизвестны, и их оценивают по выборочным данным:

Линейная функция

определяет эмпирическую линию регрессии, которая служит статистической оценкой неизвестной истинной линии регрессии.
Рассеяние вокруг линии регрессии можно оценить, используя эмпирическую среднюю дисперсию относительно линии регрессии:

Этот метод, в предположении нормальной распределённости результатов наблюдений, даёт, в некотором смысле, оптимальные результаты и позволяет проводить экстраполяцию (прогнозирование) значений величины Y по имеющимся значениям величины Х.
Литература.
Теория вероятностей и математическая статистика [Электронный ресурс]: учебное пособие/ В.С. Мхитарян [и др.].— Электрон. текстовые данные.— М.: Московский финансово-промышленный университет «Синергия», 2013.— 336 c http://www.iprbookshop.ru/17047 «IPRbooks»






