Определение УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА
МЕТОДОМ МАГНЕТРОНА
Цель работы: Экспериментально определить величину удельного заряда электрона.
Обоснование метода измерения
|
|
Магнетроном называется двухэлектродная лампа, помещенная во внешнее магнитное поле. Электроны за счет термоэлектронной эмиссии вылетают из катода, попадают в электрическое поле, определяемое конфигурацией катода-анода, и летят к аноду. Наряду с электрическим полем электроны подвергаются воздействию внешнего магнитного поля. В простейшем случае катод и анод представляют собой коаксиальные цилиндры (R к «R a ), а магнитное поле создается соленоидом, в который помещается лампа. Вектор индукции внутри лампы направлен вдоль катода и анода (рис.1). Движение электронов происходит в кольцевом пространстве, заключенном между анодом и катодом.
Отметим основные особенности движения электронов. При этом будем полагать:
1) что скорость вылета электронов из катода мала, и ею можно пренебречь, т.е. V о =0;
2) что радиус катода R к = 0, вследствие того, что радиус анода R a » R к
В отсутствие магнитного поля (В = 0) электроны летят к аноду прямолинейно по радиусам под действием силы электрического поля.
(1)
Вектор 
направлен вдоль радиуса от анода к катоду.
При включении магнитного поля 
на движущийся электрон будет действовать сила Лоренца [1].
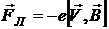(2)
где 
- заряд электрона; 
- скорость движения электрона; - индукция магнитного поля.
Согласно уравнению (2) эта сила направлена перпендикулярно скорости движения электрона и индукции магнитного поля.
На рис. 3 показано направление силы Лоренца в момент вылета электрона из катода. Под действием этой силы траектория движения из прямолинейной превращается в криволинейную (рис.2). Сила Лоренца не изменяет величины скорости, а только - ее направление [2]. Пока магнитное поле невелико, все электроны попадают на анод (рис.2,б). Чем больше индукция магнитного поля , тем меньше радиус кривизны траектории, и при некотором значении 
(критическое) траектория электрона искривляется так, что почти касается анода (рис.2,в).
 |
При
> 
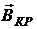электроны не достигают анода (рис.2,г), и анодный ток падает до нуля. Следует отметить, что траектории движения электронов, строго говоря, не представляют собой окружности, так как скорости электронов изменяются под действием силы электрического поля. Траектория движения в этом случае представляет собой эпициклоиду.
Рис.2
Характеристика магнетрона - зависимость анодного тока I а от индукции магнитного поля В показана на рис.4. Если исходить из предположения, что для всех электронов V 0 = 0, то зависимость I а = f (B) должна имеет вид кривой 1 (рис.4). Практически же получаемые характеристики имеют вид кривой 2 на рис.4. Это происходит от того, что электроны, движущиеся от катода к аноду, имеют различные скорости (V 0 ¹ 0), кроме того, всегда существует некоторое отступление от строгой симметрии в размерах цилиндрических электродов.
Экспериментальное определение критического магнитного поля В кр позволяет рассчитать удельный заряд электрона 
. Рассмотрим эту возможность.
В условиях критического магнитного поля В КР для электронов, попадающих на анод (определяющих величину анодного тока), справедливо следующее: на пути от катода к аноду ускоряющее электрическое поле совершит работу по перемещению электрона, равную А = е U a. Согласно закону сохранения энергии
, (3)
где U a - анодное напряжение; е - заряд электрона; m - масса электрона; V КР. - критическая скорость электрона.
 |
При коаксиальной конструкции катода и анода ускорение электрона электрическим полем осуществляется в основном в небольшой области вблизи катода. Следовательно, в остальной области ускорение электрона связано только с силой Лоренца.
Тогда, согласно второму закону Ньютона, можно записать
(4)
Так как сила Лоренца 
перпендикулярна скорости движения электрона , то 
в уравнении (4) является нормальным ускорением и, следовательно, 
, где r КР . - радиус кривизны траектории электрона при критическом магнитном поле.
Уравнение (4) может быть записано
(4х)
В условиях ВКР, r КР = 
(рис.2,в). Из соотношений (3) и (4х) следует
(5)
Так как магнитное поле создается соленоидом, длина которого намного больше его диаметра, то
, (6)
где m 0 - магнитная постоянная; m - относительная магнитная проницаемость среды (m = 1); I КР - критический ток через соленоид; N - число витков соленоида; l - длина соленоида.
Согласно (5) с учетом (6), находим
. (7)
Теперь можно, определив магнитное поле В КР или соответствующий ток соленоида I КР, при котором электроны перестают попадать на анод, пользуясь уравнением (7), рассчитать удельный заряд электрона .
