Переходные характеристики h(t) и w(t) называют временными.

Зная переходную или весовую функцию САУ, можно определить реакцию системы на произвольное входное воздействие при ННУ с помощью следующих формул:

.

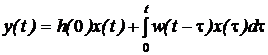Две рассмотренные формулы легко получаются друг из друга, являясь вариантами интеграла Дюамеля, или интеграла свертки. Для реальных инерционных звеньев реакция на выходе всегда отстает от входного воздействия, т.е. .

 

3.1 Линеаризация дифференциальных уравнений.

Методология математического описания САУ.

1. Система рассматривается как цепь взаимодействующих (физически и информационно) элементов, которая обладает способностью передавать физические воздействия и информационные сигналы в одном, строго определенном направлении.

2. Каждый конструктивный элемент рассматривается как преобразователь входного воздействия в выходную реакцию.

3. На основе априорных сведений о физической природе каждого элемента и закономерностях его функционирования составляется математическая модель, которая на языке соответствующей научной дисциплины отражает существенные для данной цепи взаимосвязи между входными и выходными переменными элемента.

4. При составлении математического описания всегда приходится прибегать к некоторой идеализации реальных процессов, определенным упрощениям, отбрасыванию второстепенных факторов. Удачность и допустимость этих упрощений зависят от глубины знаний исследователя системы в данной области физики и технологии, его инженерной интуиции и всегда подлежат экспериментальной проверке.

Во многих случаях нелинейные дифференциальные уравнения можно линеаризовать, т.е. заменить исходные нелинейные уравнения линейными, приблизительно описывающими процессы в системе.

Линеаризацию гладких статических характеристик можно осуществить либо по методу касательной, либо по методу секущей.

Пусть дана нелинейная характеристика (рис. 23).

Рисунок 23

 

Исходную нелинейную зависимость  можно разложить в ряд Тейлора в окрестностях точки установившегося режима, и, отбросив члены ряда выше первого порядка, получить следующую приближенную зависимость:

,

где  - значение производной функции  по x при подстановке в выражение этой производной x = x₀.

При расчете автоматических систем удобно линейные статические характеристики рассматривать в отклонениях переменных y и x от их значений y₀ и x₀.

Тогда это уравнение можно переписать в таком окончательном виде:

Произведенная линеаризация (методом касательных) имеет простую графическую интерпретацию: действительная нелинейная характеристика заменяется касательной к ней в точке, соответствующей установившемуся режиму. Коэффициент к равен тангенсу угла наклона этой касательной относительно оси абсцисс.

В более общем случае звено описывается нелинейным уравнением, включающим производные по времени от входных и выходных величин:

После разложения нелинейной функции в левой части уравнения в ряд Тейлора в точке установившегося режима, получим следующее линейное дифференциальное уравнение для приращений переменных:

Линеаризации применяется только для малых отклонений, то есть полученные в результате линеаризации уравнения пригодны для приближенного исследования только таких режимов в системах, при которых переменные величины на входе звеньев претерпевают достаточно малые отклонения от установившихся значений. Во-вторых, линеаризация применима только к непрерывно дифференцируемым нелинейностям.

 

3.2 Решение линейных дифференциальных уравнений.

При описании САУ в виде дифференциального уравнения, устанавливающего связь между входной и выходной величинами как в переходных, так и в установившихся режимах:

где  - входные величины элемента

 - выходная величина элемента

 - коэффициенты уравнения, наз. параметрами

можно применить символическую (операторную) форму записи. Переход к этой форме осуществляют введением сокращенного условного обозначения операции дифференцирования: . Соответственно к -тую производную обозначают

Тогда исходное уравнение можно записать в виде:

или:

.

Введем обозначения:

 - дифференциальный оператор при выходной величине, наз. собственным, или характеристическим оператором. Название обусловлено тем, что многочлен характеризует собственное движение элемента, т.е. движение при отсутствии внешних воздействий.

			дифференциальные операторы при входных величинах, называются операторами воздействия, операторами входа

                                                          

Тогда

.

Другая применяемая форма записи дифференциальных уравнений основана на применении преобразования Лапласа. Применим преобразование Лапласа к дифференциальному уравнению, считая, что до приложения внешнего воздействия система находилась в покое и все начальные условия равны нулю. Получим:

       Сравнивая с уравнением в символической форме, замечаем их полную аналогию. Разница только в значении символа р: в одном случае это операция дифференцирования, в другом – комплексное число.

Непосредственно методы решения линейных дифференциальных уравнений и систем с постоянными коэффициентами подробно изложены в [3].

 

3.4 Преобразования Лапласа.

Операционное исчисление – совокупность методов прикладного математического анализа, позволяющих экономными и непосредственно ведущими к цели средствами получать решения линейных дифференциальных уравнений, а также разностных.

Сущность метода. Пусть задана некоторая функция , действительной переменной , причем такая, что для нее существует преобразование Лапласа ( -преобразование):

где  - оригинал

   - изображение

 - комплексная переменная.

Свойство линейности.

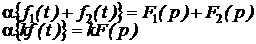
Свойство дифференцирования и интегрирования оригинала.

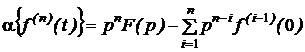
где

Обратное преобразование Лапласа.

.

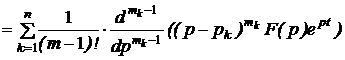
Подробно вопросы преобразования Лапласа изложены в [4].

 

Рекомендованная литература по лекции: [3, 4].

 

Лекция 4 «Частотные характеристики САУ»

4.1 Простейшие сигналы.

4.2 Передаточные функции.

 

Частотные характеристики описывают передаточные свойства элементов и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Зная частотную характеристику элемента, можно определить реакцию элемента на гармоническое воздействие любой частоты, а также на сумму гармонических воздействий различной частоты. Частотные характеристики широко используются в теории и практике автоматического управления, так как реальные возмущения, действующие на автоматические системы, могут быть представлены как сумма гармонических сигналов.

Пусть на вход линейного элемента в момент времени t =0 подано гармоническое воздействие определенной частоты w

.

Через некоторое время, необходимое для протекания переходного процесса, элемент войдет в режим установившихся вынужденных колебаний, а выходная величина y (t) будет изменяться по гармоническому закону с той же частотой w, но с отличающейся амплитудой y_m и со сдвигом 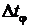 по оси времени

,

где 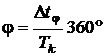 - фазовый сдвиг между входным и выходным сигналами;

 - период колебаний.

Повторяя такой эксперимент при фиксированном  для различных значений частоты (от 0 до ), можно установить, что амплитуда 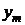 и фазовый сдвиг  выходного сигнала конкретного элемента зависят от частоты воздействия.

Подавая гармоническое воздействие на вход различных элементов, можно убедиться, что величины 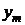и  зависят также от типа и параметров элемента.

Так как амплитуда выходного сигнала зависит ещё от амплитуды входного сигнала, то целесообразно при описании передаточных свойств элементов рассматривать отношение амплитуд .

 

4.1 Простейшие сигналы.

В теории САУ различают следующие разновдности простейших сигналов:

- гармонический (синусоидальный) ;

- периодический ;

- ступенчатый единичный сигнал ;

- дельта-функция Дирака ;

- степенная функция .