Вычисление двойного интеграла в полярной системе координат.

Напомним, что полярная система координат задаётся точкой 0 (полюсом) и лучом 0Р (полярой). Точка М в полярной системе координат задаётся двумя числами ρ и , где ρ – расстояние от точки М до полюса, а  – угол между полярой и радиус-вектором точки М. Пусть даны декартова система координат с полюсом в точке 0 и полярой 0Р, совпадающей с положительной полуосью 0Х. В этом случае формулы перехода от декартовой системы координат к полярной имеют вид:

Далее имеем:

Где D* отображается в D, а якобиан имеет вид

При вычислении интегралов не обязательно изображать на чертеже область D*.

Рассмотрим это более подробно.

Будем предполагать, что область не содержит внутри полюс О и любой луч, который исходит из полюса пересекает границу 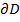 не более, чем в двух точках

Теперь рассмотрим случай, когда полюс внутри области интегрирования D, а любой луч, который исходит из полюса, пересекает  в одной точке

 

y

 

Пример 4. Вычислить объем тела, ограниченного плоскостью X0Y и поверхностью z= 1-x²-y².

1

z

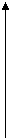Поверхность z= 1-x²-y² пересекается с плоскостью X0Y (z=0) по окружности 1-x²-y² =0; x²+y²=1. Данное тело проецируется на плоскость X0Y в круг с центром в начале координат радиуса 1.

1

y

x

 

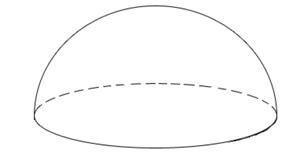
Следовательно:

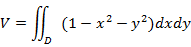
При вычислении данного интеграла удобно перейти к полярным координатам.

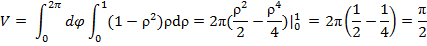
Так как внутренний интеграл не содержит , то внешний интеграл по  можно вычислять сразу.

 

Применение двойных интегралов

А) Вычисление объемов тел

Данное тело спроецируем на одну из координатных плоскостей. Пусть для определенности тело спроецировано на плоскость X0Y в область D. Будем предполагать, что любая прямая, проходящая через D параллельно оси 0Z пересекает границу тела не более чем в двух точках. Тогда граница тела разобьется на нижнюю и верхнюю части, уравнения которых запишем в виде Z=f₁(x,y)

 и Z=f₂(x,y). В этом случае объем тела находится по формуле

 

Б) Вычисление площади поверхности

Пусть Q есть участок поверхности Z=f(x,y), а D проекция этого участка на плоскость X0Y.

Площадь поверхности Q вычисляется по формуле:

D

Q

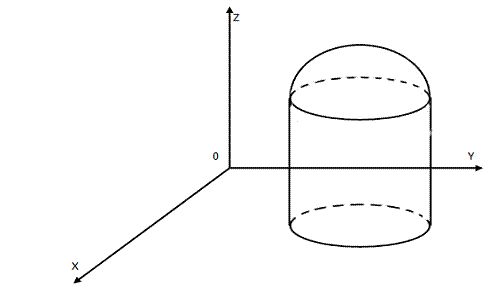
Пример 5. Вычислить объем тела, ограниченного поверхностями  и Z=5

Решение.

  

 

 

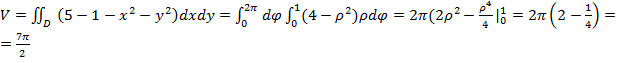
Пример 6. Вычислить площадь поверхности Z=2-x-у, вырезанной цилиндром

Решение: Уравнение цилиндра запишем в виде: . Направляющей данного цилиндра является окружность с центром в точке О (1,0) и радиуса 1, а образующая параллельна оси OZ. Часть поверхности, которая вырезается из плоскости Z=2-x-y данным цилиндром спроецируется на плоскость X0Y в круг с центром в точке О(1,0) радиуса 1. Теперь найдём .

Имеем:

 

где S₁- площадь области D. Известно,что S₁₌ ,Следовательно: S=