Лабораторная работа № 2 комплексные числа

ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ

Вариант 1

1) 2) 3)

 

Вариант 2

1) 2) 3)

 

Вариант 3

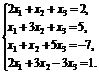1) 2) 3)

 

Вариант 4

1)  2) 3)

 

Вариант 5

1) 2) 3)

Вариант 6

1) 2) 3)

Вариант 7

1)  2) 3)

Вариант 8

1) 2) 3)

Вариант 9

1)  2) 3)

 

Вариант 10

1)  2) 3)

 

Вариант 11

1) 2)  3)

Вариант 12

1) 2)    3)

 

Вариант 13

1) 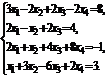2)    3)

 

ЛАБОРАТОРНАЯ РАБОТА № 2 КОМПЛЕКСНЫЕ ЧИСЛА

Комплексное число в алгебраической форме имеет вид а+bi (1), где а и b – действительные числа, а i – мнимая единица, причем i²= -1. В записи (1) bi называется мнимой частью, а – действительной частью комплексного числа. Два комплексных числа называются равными только в том случае, когда равны их мнимые и действительные части.

Для комплексных чисел вида (1) имеют место следующие операции:

а) сложение (вычитание): ;

б) умножение: ;

в)

(деление возможно только в том случае, когда c+di≠0 (c²+d²≠0)).

Введенные операции обладают всеми свойствами аналогичных операций над действительными числами. Следует обратить внимание, что i²= -1, i³= -i, i⁴=1, i⁵=i, i⁶= -1, ….

Комплексные числа можно отождествить (изобразить) точками некоторой комплексной плоскости, в которой расположим прямоугольную систему координат OXY, причем OX назовем действительной осью и на ней будем откладывать действительную часть комплексного числа, а ось OY – мнимой осью, на ней будем откладывать мнимую часть. Комплексное число а+bi будет точкой этой плоскости.

Рис.1

Кроме алгебраической формы для комплексных чисел существует еще тригонометрическая форма. Чтобы получить эту форму для числа z=a+bi, обозначим r – расстояние от начала координат до числа z (рис.1), j - угол между положительным направлением оси ОХ и отрезком OZ. Тогда, очевидно, из ∆OAZ получим, что a=rcosφ, b=rsinφ и a+bi=rcosφ+irsinφ. Форма z=r(cosφ+isinφ) называется тригонометрической формой комплексного числа, r – модулем z и записывается r=|z|, а φ – аргументом z, или φ=argz.

Для приведения комплексного числа а+bi к тригонометрической форме используют формулы cosφ=  и sinφ= , из которых находят значения φ, а .

Пример 1. Найти тригонометрическую форму комплексного числа A. ; Б. 5i; В. 5+3i.

Решение. А. Так как , то а=1, b= , . Тогда cosφ= ; sinφ= . Откуда следует, что φ= . Окончательно получаем, что .

Б. Изобразим число 5i на комплексной плоскости. Очевидно, что оно расположено на оси ОY, т.е. модуль r=5, а аргумент равен . Записываем число 5i в тригонометрической форме .

В. Модуль z числа 5+3i равен , аргумент φ его находим из соотношений cosφ= , sinφ=  по таблицам. Записываем число 5+3i в тригонометрической форме (cosφ+isinφ).

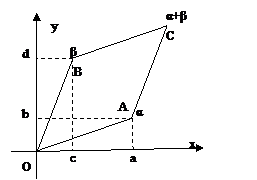
Сложение и вычитание комплексных чисел можно истолковать геометрически. Пусть даны числа α=a+bi, β=c+di. Соединим отвечающие им точки на комплексной плоскости с началом координат и построим на этих отрезках, как на сторонах, параллелограмм. Четвертой вершиной этого параллелограмма будет точка, которая отвечает числу α+β (рис.2).

Рис.2

	Рис.2

 

Таким образом, сложение комплексных чисел геометрически выполняется по правилу сложения векторов, выходящих из начала координат, модуль суммы векторов α и β равен длине диагонали ОС параллелограмма АОВС.

Вычитание комплексных чисел можно заменить сложением α-β=α+(-β), поэтому геометрически разность векторов можно описать так. На комплексной плоскости отмечаем точки А, В, Д, соответствующие числам α, β и –β. Складываем числа α и –β, т.е. строим параллелограмм АОДК (рис.3). Точка К, четвертая вершинпараллелограмма отвечает числу α-β.

 Модуль числа α-β равен длине диагонали ОК параллелограмма АОДК. Очевидно, параллелограммы АОВС и

Рис.3

АОДК конгруэнтны. Поэтому модуль разности равен также длине диагонали АВ параллелограмма АОВС. Известно, что │α–β│=k, то числу α отвечает точка, отстоящая от точки В на расстоянии k. Тогда точки, изображающие числа z, удовлетворяющие равенству │α–β│=k, есть точки, отстоящие от точки В, изображающей число β, на расстояние k: они составляют окружность на комплексной плоскости с центром в точке В радиуса k.

Действия умножения, деления, возведения в степень, извлечения корня удобно производить, когда эти числа заданы в тригонометрической форме следующим образом:

1. [r(cosφ+isinφ)][R(cosψ+isinψ)]=rR(cos(φ+ψ)+isin(φ+ψ));

 

2. ;

 

 

3. [r(cosφ+isinφ)]ⁿ=rⁿ(cosnφ+isinnφ);

 

4.  k=0,1,…,n-1.

Пример 3. Найти .

Решение. Запишем число  в тригонометрической форме

. Применим формулу Муавра

Пример 4. Найти .

Решение. Запишем число i в тригонометрической форме . Применяем формулу

 

Записываем значения корня последовательно для k=0,1,2:

Пример 5. Найти геометрическое место точек, изображающих числа z, удовлетворяющих неравенству: А. │z│≤5, Б. 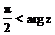≤π,
В. │z–3i│>2.

Решение.

А. Так как модуль комплексного числа есть расстояние от начала координат до точки, изображающей его, то точки, изображающие комплексные числа с условием │z│≤5, составляют круг радиуса 5 с центром в начале координат. Точки окружности также принадлежат этой области.

Б. Так как аргумент комплексного числа – это угол, составленный положительным направлением оси ОХ и отрезком, соединяющим начало координат с точкой, изображающей его, то геометрическое место точек, изображающих числа z, удовлетворяющее соотношению 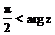≤π, есть множество точек второго координатного угла. Точки оси ОХ входят, а точки оси ОY не входят в эту область.

В. Из геометрического смысла вычитания следует, что такие точки составляют внешнюю часть окружности радиуса 2 с центром в точке А, отвечающей числу 3i. Точки окружности в эту область не входят (рис.4).

Рис.4

Извлечение квадратного корня из комплексного числа a+bi удобно производить следующим образом. Пусть . Из равенства a+bi=(u+vi)² следует . Из этой системы уравнений нам надо найти u, v. Возведем в квадрат обе части каждого из этих уравнений и сложим, получаем (u²–v²)²+4u²v²=a²+b², откуда . Учитывая, что u²–v²=a, находим . Тогда . Полученные значения u, v нельзя комбинировать между собой произвольным образом, так как знак произведения uv должен совпадать со знаком числа b. Это дает две возможные комбинации u, v, т.е. два числа вида u+iv, которые являются значениями квадратного корня из числа a+bi. Эти числа отличаются друг от друга знаком.

Пример 6. Найти .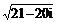

Решение. Обозначим 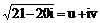. Для вычисления u и v применяем формулы

.

Знаки u и v должны быть различными, так как b= -20<0, поэтому .

 

Пример 7. Решить уравнение x²– (2+i)x+(–1+7i)=0.

 

Решение. По формуле корней квадратного уравнения , или . Извлечение квадратного корня производим как и в предыдущем примере: .

Таким образом, , поэтому,

Ответ: x₁= -1+2i; x₂=3-i.

 

ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ

Вариант 1

1. Вычислить: 1) ; 2) ; 3) .

 

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z–i|>1; 2) |z–i+3|≤3.

 

3. Решить уравнение x²– (2+i)x+(–1–5i)=0.

 

Вариант 2

1. Вычислить: 1) ; 2) ; 3) .

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z–2+3i|≤3; 2) |z+i|>4.

 

3. Решить уравнение x²+(2+2i)x+3–2i=0.

 

Вариант 3

1. Вычислить: 1) ; 2) ; 3) .

 

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z–2+i|≤2; 2) |z+i|=2.

 

3. Решить квадратное уравнение x²+(–1+3i)x–2i–2=0.

 

Вариант 4

1. Вычислить: 1) ; 2) ; 3) .

 

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z+2i|>3; 2) |z–1–2i|≤1.

 

3. Решить уравнение x²+(i–1)x+6+2i=0.

 

Вариант 5

1. Вычислить: 1) ; 2) ; 3) .

 

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z+2i–3|>2; 2) |z–3i|≤3.

 

3. Решить уравнение x²+(3+4i)x+5+15i=0.

 

Вариант 6

1. Вычислить: 1) ; 2) ; 3) .

 

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z–2i–3|>2; 2) |z+3i|≤1.

 

3. Решить уравнение x²– (2i+1)x+8+4i=0.

 

Вариант 7

1. Вычислить: 1) ; 2) ; 3) .

 

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z+1+2i|≥1; 2) |z–3i|<3.

 

3. Решить уравнение x²+(–2+3i)x–3i–1=0.

 

Вариант 8

1. Вычислить: 1) ; 2) ; 3) .

 

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z+2i|≤1; 2) |z+1+i|>3.

 

3. Решить уравнение x²–х(i–2)+12–8i=0.

 

 

Вариант 9

1. Вычислить: 1) ; 2) ; 3) .

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z+4+2i|>1; 2) |z–5i|≤3.

 

3. Решить уравнение x²+(–2+3i)x–3i–1=0.

 

Вариант 10

1. Вычислить: 1) ; 2) 3) .

 

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z–1+3i|≤2; 2) |z+2i|>2.

 

3. Решить уравнение x²–х(2i–5)+3–15i=0.

 

Вариант 11

1. Вычислить: 1) ; 2) ; 3) .

 

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z–i+2|≤1; 2) |z–4i|>1.

 

3. Решить уравнение x²+5x+7–i=0.

 

Вариант 12

1. Вычислить: 1) ; 2) ; 3) .

 

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z+i+2|≤1; 2) |z+3i|>3.

 

3. Решить уравнение x²– (5+4i)x+3+11i=0.

Вариант 13

1. Вычислить: 1) ; 2) ; 3) .

 

2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам: 1) |z+i+2|≥3; 2) |z–i+1|<1.

 

3. Решить уравнение x²– (4+i)x–8i+6=0.