Матрицы.
1.1. Операции с матрицами: равенство матриц; сложение матриц; умножение матрицы на число; перемножение матриц. Основные свойства операций сложения и умножения матриц.
1.2. Транспонирование матриц.
1.3. Квадратные, треугольные, диагональные, симметричные матрицы. Единичная матрица.
Определители.
2.1. Понятие перестановки. Инверсия, транспозиция. Четность (нечетность) перестановки.
2.2. Определитель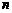 
-го порядка. Правила Саррюса вычисления определителей 2-го и 3-го порядков.
2.3. Основные свойства определителей.
Определители (продолжение).
3.1. Миноры и алгебраические дополнения.
3.2. Разложение определителя по строке (столбцу).
3.3. Обратная матрица, ее нахождение. Невырожденные и вырожденные матрицы. Критерий обратимости матрицы.
3.4. Определитель произведения квадратных матриц.
Использование матриц и определителей при решении линейных алгебраических систем.
4.1. Совместные, несовместные линейные системы. Матричная запись линейной системы.
Невырожденные линейные системы.
4.2. Решение невырожденных систем по правилу Крамера и с помощью обратной матрицы.
Метод Гаусса решения линейных алгебраических систем.
5.1. Приведение системы к треугольному виду.
5.2. Выделение свободных и базисных неизвестных.
5.3. Получение общего решения системы или вывода о несовместности системы.
6. Векторы в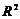 
, 
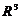. Скалярное произведение векторов.
6.1. Декартовы координаты на плоскости и пространстве. Вектор как направленный отрезок.
6.2. Сложение векторов. Умножение вектора на число. Проекция вектора на ось.
6.3. Условие коллинеарности двух векторов (
).
6.4. Скалярное произведение векторов, его свойства, координатное выражение.
6.5. Условие ортогональности двух векторов (
).
Векторное и смешанное произведение векторов.
7.1. Деление отрезка в данном отношении.
7.2. Компланарные, некомпланарные тройки векторов. Ориентация тройки векторов.
7.3. Векторное произведение: определение; свойства; координатное выражение.
7.4. Смешанное произведение: определение; свойства; координатное выражение.
7.5. Условие компланарности тройки векторов (
).
Прямая на плоскости.
8.1. Понятие об уравнениях линии на плоскости.
8.2. Различные виды задания прямой на плоскости (общее уравнение, 
, канонические уравнения, параметрические уравнения).
8.3. Основные задачи по нахождению прямой на плоскости: через точку перпендикулярно вектору (прямой); через точку параллельно вектору (прямой);через две точки.
8.4. Взаимное расположение двух прямых.
8.5. Расстояние от точки до прямой.
Плоскость и прямая в пространстве.
9.1. Общее уравнение плоскости. Нормальный вектор.
9.2. Прямая в пространстве: канонические, параметрические уравнения.
9.3. Основные задачи по нахождению плоскости: через точку перпендикулярно вектору; через три точки; через точку параллельно паре векторов.
9.4. Основные задачи по нахождению прямой в пространстве: через две точки; через точку перпендикулярно плоскости, через точку параллельно вектору (прямой).
9.5. Расстояние от точки до плоскости.
9.6. Взаимное расположение двух прямых в пространстве.
Кривые второго порядка.
10.1. Эллипс. Геометрическое определение, вывод канонического уравнения. Полуоси, эксцентриситет, график.
10.2. Гипербола. Геометрическое определение. Полуоси, эксцентриситет, асимптоты, график.
10.3. Парабола. Геометрическое определение. Параметр параболы, график.
