| № п/п | Значения признака x | Значения признака y |
| 1 | x1 | y1 |
| 2 | x2 | y2 |
| … | … | … |
| n | xn | yn |
Значения 
из каждой строки рассматривают как координаты точки 
на плоскости. Совокупность всех точек называется полем корреляции. По характеру расположения точек поля корреляции формулируется предварительный вывод о наличии связи между признаками, её направлении (прямая или обратная) и форме (алгебраической функции, описывающей данную связь).
2) Эмпирический коэффициент детерминации 
характеризует долю факторной дисперсии[13] в общей дисперсии результативного признака и рассчитывается по формуле:
Эмпирическое корреляционное отношение 
характеризует тесноту связи между признаками и рассчитывается по формуле:
где 
межгрупповая дисперсия, характеризующая систематическую вариацию[14] результативного признака под влиянием признака-фактора, положенного в основание группировки:
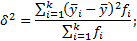
– общая дисперсия результативного признака, измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:
Эмпирическое корреляционное отношение 
изменяется в пределах от 0 до 1 и характеризуетстепеньвлияния группировочного признака на вариацию результативного признака (тесноту связи между признаками):
· если 
, то группировочный признак не оказывает влияния на результативный;
· если 
, то результативный признак варьирует только под влиянием группировочного признака, а влияние прочих факторов равно нулю;
· чем ближе к 1 его величина, тем теснее связь между признаками.
Для выводов о степени тесноты связи используется шкала Чеддока:
| Значение показателя | 0-0,1 | 0,11-0,3 | 0,31-0,5 | 0,51-0,7 | 0,71-0,9 | 0,91-0,99 | 0,991-1 |
| Характеристика связи | отсутствует | слабая | умеренная | заметная | тесная | сильная | функцио-нальная |
Для расчета общей дисперсии 
по несгруппированным данным строится таблица 3.2:
Таблица 3.2
Расчёт общей дисперсии результативного признака
| № п/п | Наименование результативного признака, ед. измерения (yi) | 
| 
|
| 1 | |||
| ... | |||
| n | |||
| Итого | Х | ||
| Средняя | Х | ||
|
| |||
...Для расчета межгрупповой дисперсии рекомендуется построить таблицу 3.3, используя результаты построения аналитической группировки в Задании 1:
Таблица 3.3
Расчёт межгрупповой дисперсии результативного признака
| № п/п | Группы субъектов РФ по.... (наименование группировочного признака, ед. измерения) (x i) | Число субъектов РФ (fi) | В среднем на один субъект РФ,... (ед. измерения) ( )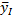
| 
| 
| 
|
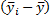
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| Итого | Х | Х | Х | |||
|
| ||||||
=...Для оценки тесноты предполагаемой линейной связи коэффициент парной корреляции (
рассчитывается по формуле:
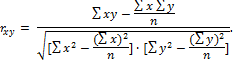
Для удобства его вычисления составляется таблица 3.4, в итоговой строке производится расчет необходимых для подстановки в формулы сумм:
Таблица 3.4
