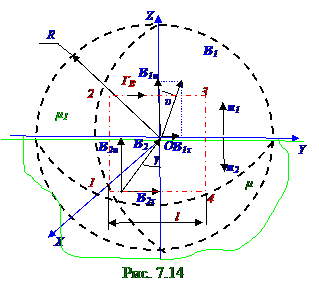
H1, H2 напряжённости магнитного поля имеют следующую связь с модулями B1, B2 векторов

H1, H2 напряжённости магнитного поля внутри соленоида одинаково направлены и перпендикулярны вертикальной поверхности парамагнетика, т.е. имеют только нормальные составляющие, на границе этого парамагнетика векторы нормальных составляющих

H _{1 n} и H _{2 n} напряжённости H магнитного поля сохраняют своё направление, но изменяют величину своего модуля пропорционально μ₂/ μ₁ отношению магнитных проницаемостей.

   Вследствие этого соотношение между модулями H₁, H₂ векторов H ₁, H ₂ напряжённости магнитного поля внутри соленоида на границе раздела парамагнетика с вакуумом с магнитными проницаемостями соответственно μ₁ и μ₂ имеет следующий вид:                 H₁/ H₂ = μ₂/μ₁,         (5.3)

где μ₁ = 1 - магнитная проницаемость вакуума; μ₂ > 1 - магнитная проницаемость парамагнетика.

   Для случая μ₂ > μ₁ на границе раздела парамагнетика с вакуумом векторы (рис. 07. 1.10) нормальных составляющих H ₁ и H ₂ напряжённости магнитного поля сохраняют своё направление, но модуль (5.3) H₁ больше H₂ в μ₂/μ₁ раз.

   Согласно (7.127) из раздела 7.2 " Магнитное поле в веществе " модули H₁, H₂ векторов

H1, H2 напряжённости магнитного поля имеют следующую связь с модулями B1, B2 векторов

B ₁, B ₂ индукции магнитного поля внутри соленоида вдалеке от границы парамагнетика с вакуумом:                                                                              B₁   = μ₀ μ₁ H₁; B₂ = μ₀ μ₂ H₂ ↔ B₁ / B₂ = μ₁/μ₂,    (5.4) где H₁ = H₂ - согласно (5.1), (5.2) равные вдалеке от границы парамагнетика с вакуумом модули

H₁, H₂ векторов H ₁, H ₂ напряжённости магнитного поля; μ₁ = 1 - магнитная проницаемость вакуума; μ₂ > 1 - магнитная проницаемость парамагнетика.

   Согласно (5.4) модули B₁, B₂ векторов B ₁, B ₂ индукции магнитного поля внутри соленоида вдалеке от границы парамагнетика с вакуумом прямо пропорциональны своим магнитным проницаемостям.

       Согласно (7.128) из раздела 7.2 " Магнитное поле в веществе " с учётом того, что векторы

B ₁, B ₂ индукции магнитного поля внутри соленоида одинаково направлены и перпендикулярны вертикальной поверхности парамагнетика, т.е. имеют только нормальные составляющие, на границе этого парамагнетика векторы нормальных составляющих B _{1 n} и B _{2 n} индукции  магнитного поля сохраняют своё направление и величину своего модуля.

   Вследствие этого соотношение между модулями B₁, B₂ векторов B ₁, B ₂ индукции магнитного поля внутри соленоида на границе раздела парамагнетика с вакуумом с магнитными проницаемостями соответственно μ₁ = 1 и μ₂ > 1 имеет следующий вид:                                                  B₁  = B₂,         (5.5)

Согласно (7.126) из раздела 7.2 "Магнитное поле в веществе" модули J1, J 2 векторов J1, J 2 намагниченности имеют следующую связь с модулями H1, H2

т.е. на границе раздела парамагнетика с вакуумом (рис. 7. 10) векторы B ₁, B ₂ индукции магнитного поля сохраняют своё направление и модуль.

           

векторов H ₁, H ₂ напряжённости магнитного поля внутри соленоида вдалеке от границы парамагнетика с вакуумом:                                                      J₁ = χ₁ H₁ = 0; J₂ = χ₂ H₂,        (5.6)

где χ₁ = μ₁ -1 = 0 - магнитная восприимчивость вакуума; χ₁ = μ₂ -1 > 0 - магнитная восприимчивостьпарамагнетика.

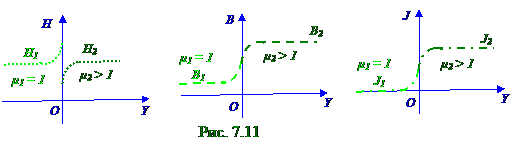
       На рис. 7.11 изображены примерные графики H, B и J модулей векторов H, B и J соответственно напряжённости, индукции магнитного поля и намагниченности внутри соленоида  в области пространства, где отсутствует парамагнетик, т.е. где вакуум при y < 0, и   где присутствует парамагнетик при y > 0.

 

Задача 6

Векторы B индукции магнитного поля (рис. 7.12) в вакууме вблизи плоской поверхности магнетика с μ магнитной проницаемостью параллельны  OYZ плоскости и направлены под υ углом относительно OZ оси, перпендикулярной этой плоской поверхности магнетика. Найти поток Ф H вектора H напряжённости магнитного поля через воображаемую сферу R радиуса, O центр которой лежит на поверхности магнетика, а также определить

 

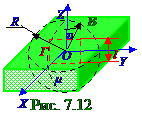
Г _B циркуляцию вектора B по воображаемому квадратному контуру l длиной, наполовину расположенному в магнетике, а наполовину в вакууме. Дано: υ; R; B; l; μ / Ф _H =? Г _B =?

       Согласно (7.17) из раздела 7.1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях " поток Ф _H1  вектора H₁ напряжённости магнитного поля (рис. 7.1.13) через воображаемую верхнюю полусферу сферу R радиуса образует H_{1 n} нормальная составляющая этого H₁ вектора, вследствие чего этот поток Ф _H1 имеет следующий вид:

                                                      Ф _H1 = ∫ H₁ d S = π R²H_1n   = π R²H ₁ cosυ = (B/μ ₀ )π R²cosυ,         (6.1)

                                                                S_в

где S_в - площадь поверхности полусферы; H ₁ = (B/μ₀ ) - связь (7.125) из раздела 7.2 " Магнитное поле в веществе " модуля H₁ вектора H ₁ напряжённости магнитного поля с модулем B вектора B индукции магнитного поля в вакууме; π R² - площадь круга, поверхность которого

                  

перпендикулярна к H1 n нормальной составляющей вектора H1 напряжённости магнитного поля              (рис. 7.1.13) через воображаемую верхнюю полусферу. Магнитный поток Ф H1 > 0, т.к.  вектор H1 напряжённости однородного магнитного поля ориентирован в одну сторону с единичным n1 нормальным вектором к поверхности круга π R2 площадью в вакууме. Согласно (7.17) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" поток Ф H2 вектора H2 напряжённости магнитного поля (рис. 7.1.13) через воображаемую нижнюю полусферу сферу R радиуса образует H2 n нормальная составляющая этого H2 вектора, вследствие чего этот поток Ф H2 имеет следующий вид:

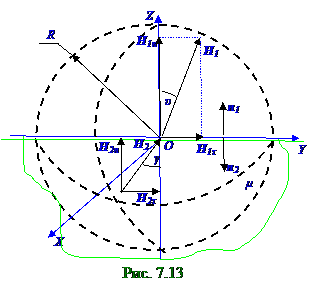
       Ф _H2= - ∫ H₂ d S = -π R² H_{2 n}   = - π R² H ₂ cosγ = - π R² H_{2 τ} cosγ/ sinγ = - π R² H_{2 τ}/ tgγ = - π R² H_{1 τ}/ tgγ =

                   S_в                                                  

                                          = - π R²(B/μ₀ ) sinυ/ tgγ = - π R²(B/μ₀ ) sinυ/μ tgυ= - π R²(B/μ₀ μ) cosυ,                  (6.2)

где μ tgυ = tgγ -соотношение (7.134) из раздела 7.2 " Магнитное поле в веществе ", связывающее υ, γ углы падения соответственно в вакууме и магнетике H₁ и H ₂ векторов.

       Магнитный поток Ф _H2 < 0, т.к. вектор H ₂ напряжённости однородного магнитного поля ориентирован в противоположную сторону с единичным n₂ нормальным вектором к поверхности круга π R² площадью в магнетике.

       Поток Ф _H  вектора H напряжённости магнитного поля через воображаемую сферу R радиуса,

O центр которой лежит на поверхности магнетика, складывается из (6.1) Ф _H1 и (6.2) Ф _H2 потоков, вследствие чего этот поток Ф _H имеет следующий вид: Ф _H = Ф _H1 + Ф _H2= π R² Bcosυ[(μ - 1)/μ₀ μ].           (6.3) 

                                                                                     

Циркуляция векторов B1, B2 индукции магнитного поля по   1 - 2 - 3 -4 контуру   в области пространства на границе вакуума с магнетиком с соответственно μ1 = 1 и μ > 1 магнитными проницаемостями при отсутствии вектора   j плотности макроскопических или токов проводимости на поверхности границы раздела магнетика с вакуумом будет иметь следующий вид:                                                   ∫ B dl = ∫B1τ dl + ∫B2τ dl = B1τ l - B2τ l =                 1-2 -3-4     1-2  3-4                    = B l sinυ - B1τμ l sinυ = B l sinυ(1 - μ),      (6.4) где B2τ = B1τμ        - соотношение (7.133) из раздела 7.2 "Магнитное поле в веществе" между тангенциальными составляющими вектора B индукции магнитного поля на границе раздела магнетика с вакуумом.