Министерство образования и науки Российской федерации
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Ростовский государственный строительный университет»
Утверждено
на заседании кафедры физики
21 декабря 2007 г.
ИНФОРМАЦИОННО-методическИЕ УКАЗАНИЯ К КОМПЬЮТЕРНОМУ ТЕСТИРОВАНИЮ ПО ФИЗИКЕ.
ЧАСТЬ II. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
Ростов-на-Дону
2008
УДК 531.383
Информационно-методические указания к компьютерному тестированию по физике. Часть II. Механические колебания и волны.
– Ростов н/Д: Рост. гос. строит. ун-т, 2008. – 11 с.
Содержатся тестовые задания для проверки уровня подготовки студентов по курсу физики, а также необходимый теоретический материал для самостоятельной работы студентов при подготовке к защите лабораторных работ физического практикума, к промежуточной и итоговой аттестациям студентов, к сдаче зачетов и экзаменов.
Предназначены для студентов всех специальностей РГСУ, предусматривающих изучение курса физики.
Составители: проф. Н.Н.Харабаев,
ст. преп. И.В.Мардасова
Рецензент: проф. А.Н.Павлов
Редактор Н.Е.Гладких
Темплан 2008 г., поз. 196
Подписано в печать 14.03.08.
Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л. 0,7.
Тираж 100 экз. Заказ
___________________________________________________________
Редакционно-издательский центр
Ростовского государственного строительного университета
334022, Ростов-на-Дону, ул. Социалистическая, 162.
© Ростовский государственный
строительный университет, 2008
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
ЗАДАНИЕ № 1
Материальная точка совершает гармонические колебания с амплитудой А = 4 см и частотой ν= 2 Гц. Если смещение точки в момент времени, принятый за начальный, равен своему максимальному значению, то точка колеблется в соответствии с уравнением …
ВАРИАНТЫ ОТВЕТОВ:
1) x= 0,04cos πt; 3) x= 0,04cos(π/2) t;5) x= 0,04cos 4πt;
2) x= 0,04sin πt; 4) x= 0,04sin(π/2) t;6) x= 0,04sin 4πt.
ЗАДАНИЕ № 2
На рисунках изображены зависимости от времени координаты и скорости материальной точки, колеблющейся по гармоническому закону.
 
|
Циклическая частота колебаний точки равна …
1) 1 с-1 ; 2) 2 с-1; 3) 3 с-1; 4) 4 с-1.
ЗАДАНИЕ № 3
На рисунках изображены зависимости от времени координаты и ускорения материальной точки, колеблющейся по гармоническому закону.
 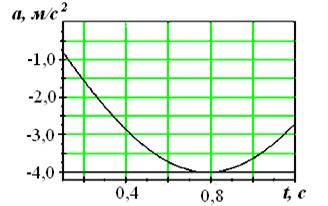
|
Циклическая частота колебаний точки равна …
1) 1 с-1 ; 2) 2 с-1; 3) 3 с-1; 4) 4 с-1.
ЗАДАНИЕ № 4
На рисунках изображены зависимости от времени скорости и ускорения материальной точки, колеблющейся по гармоническому закону.
 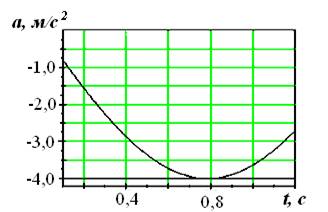
|
Циклическая частота колебаний точки равна …
1) 1 с-1 ; 2) 2 с-1; 3) 3 с-1; 4) 4 с-1.
ЗАДАНИЕ № 5
Частица может колебаться вдоль оси x под действием результирующей силы  с амплитудой А и частотой w, где k – положительная константа. В момент, когда x=А/ 2, скорость частицы будет равна:
с амплитудой А и частотой w, где k – положительная константа. В момент, когда x=А/ 2, скорость частицы будет равна:
ВАРИАНТЫ ОТВЕТОВ:
1) 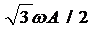 ; 2)
; 2)  ; 3)
; 3) 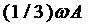 ;
;
4)  ; 5)
; 5)  .
.
---------------------------
Указания к заданиям № 1 – 5
Гармонические колебания величины 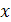 (координаты материальной точки) описываются уравнением:
(координаты материальной точки) описываются уравнением:
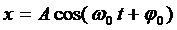 , где
, где
А – амплитуда колебаний – максимальное значение колеблющейся величины;
ω0 – круговая (циклическая) частота;
 – фаза колебаний в момент времени t;
– фаза колебаний в момент времени t;
j 0 – начальная фаза колебаний.
Скорость материальной точки:  .
.
Ускорение материальной точки: 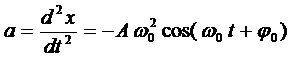 .
.
Максимальные значения смещения x, скорости u, ускорения a:
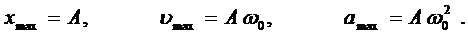
ЗАДАНИЕ № 6
Частица массы m, движущаяся вдоль оси x, имеет потенциальную энергию U(x)=a+bx2, где a и b – положительные константы. Начальная скорость частицы равна V0 в точке x= 0. Частица совершает гармонические колебания с частотой, определяемой значениями:
ВАРИАНТЫ ОТВЕТОВ:
1) только b и m;
2) только b и a;
3) b, a, m и V0;
4) только b, a и m;
5) только b.
---------------------------
Указание
Круговая частота гармонического колебания частицы массой m вдоль оси х:
 , где k – коэффициент упругости в соотношении
, где k – коэффициент упругости в соотношении 
(Fx – возвращающая сила: 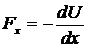 , где U (x) – потенциальная энергия).
, где U (x) – потенциальная энергия).
ЗАДАНИЕ № 7
Уравнение пружинного маятника 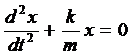 является дифференциальным уравнением …
является дифференциальным уравнением …
ВАРИАНТЫ ОТВЕТОВ:
1) cвободных незатухающих колебаний;
2) cвободных затухающих колебаний;
3) вынужденных колебаний.
ЗАДАНИЕ № 8
Уравнение пружинного маятника 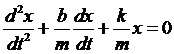 является дифференциальным уравнением…
является дифференциальным уравнением…
ВАРИАНТЫ ОТВЕТОВ:
1) свободных незатухающих колебаний;
2) свободных затухающих колебаний;
3) вынужденных колебаний.
ЗАДАНИЕ № 9
Уравнение пружинного маятника  является дифференциальным уравнением…
является дифференциальным уравнением…
ВАРИАНТЫ ОТВЕТОВ:
1) свободных незатухающих колебаний;
2) свободных затухающих колебаний;
3) вынужденных колебаний.
---------------------------
Указания к заданиям № 7 – 9
Дифференциальное уравнение вынужденных гармонических колебаний пружинного маятника:
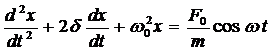 ,
,
где δ – коэффициент затухания колебаний под действием силы сопротивления: 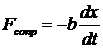 ;
;
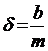 , где b – коэффициент сопротивления, m – масса груза;
, где b – коэффициент сопротивления, m – масса груза;
ω0 – циклическая частота свободных незатухающих колебаний пружинного маятника в отсутствии сил сопротивления и внешней вынуждающей силы;  , где k – жесткость пружины;
, где k – жесткость пружины;
F 0 – амплитуда вынуждающей силы;
ω – циклическая частота вынуждающей силы.
ЗАДАНИЕ № 10
Маятник настенных механических часов представляет собой легкий стержень с грузиком. Для регулировки точности хода часов грузик можно перемещать по стержню. Как изменится период колебаний маятника, если грузик переместить с конца стержня на середину?
ВАРИАНТЫ ОТВЕТОВ:
1) увеличится в  pаз;
pаз;
2) уменьшится в  pаз;
pаз;
3) увеличится в 2 pаза;
4) уменьшится в 2 pаза;
5) увеличится в 4 pаза.
ЗАДАНИЕ № 11
На рисунке приведены 2 маятника, отличающиеся положением грузов на невесомом стержне. Укажите верные утверждения для этих маятников.
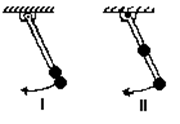
А. Момент инерции маятника I больше момента инерции маятника II.
B. Оба маятника имеют одинаковую частоту колебаний.
C. Период колебаний маятника I больше периода колебаний маятника II.
ВАРИАНТЫ ОТВЕТОВ:
1) только С;
2) А, C;
3) А, B;
4) только А;
5) только В.
---------------------------
Указания к заданиям № 10, 11
Момент инерции материальной точки массой m относительно оси вращения ОО’:
 , где r – расстояние от этой точки до оси вращения ОО’.
, где r – расстояние от этой точки до оси вращения ОО’.
Момент инерции системы N материальных точек относительно оси ОО’:
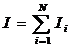 , где Ii – момент инерции i – й материальной точки относительно оси ОО’.
, где Ii – момент инерции i – й материальной точки относительно оси ОО’.
Теорема Штейнера: если момент инерции тела относительно оси ОО’, проходящей через центр масс данного тела, равен I С, то момент инерции того же тела относительно оси О1О1’, параллельной оси ОО’, равен:  , где m – масса тела; а – расстояние между рассматриваемыми осями.
, где m – масса тела; а – расстояние между рассматриваемыми осями.
Период колебаний физического маятника:  ,
,
где I – момент инерции физического маятника относительно оси вращения,
m – масса физического маятника,
l – расстояние от центра масс физического маятника до его оси вращения.
СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
ЗАДАНИЕ № 12
Складываются два гармонических колебания одного направления с одинаковой частотой и равными амплитудами А0. При разности фаз Δφ=π амплитуда результирующего колебания …
ВАРИАНТЫ ОТВЕТОВ:
1) 0; 2)  А0; 3) 2 А0; 4) 5/2 А0.
А0; 3) 2 А0; 4) 5/2 А0.
ЗАДАНИЕ № 13
Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами А0. При разности фаз Δφ=π/ 2 амплитуда результирующего колебания …
ВАРИАНТЫ ОТВЕТОВ:
1) 0; 2)  А0; 3) 2 А0; 4) 5/2 А0.
А0; 3) 2 А0; 4) 5/2 А0.
ЗАДАНИЕ № 14
Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз …
ВАРИАНТЫ ОТВЕТОВ:
1) 0; 2) p / 2; 3) p; 4) 3 p / 2.
ЗАДАНИЕ № 15
Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет минимальную амплитуду при разности фаз …
ВАРИАНТЫ ОТВЕТОВ:
1) 0; 2) p / 2; 3) p ; 4) 3 p / 2.
---------------------------
Указание к заданиям № 12 – 15
При сложении гармонических колебаний c амплитудами А1 и А2 одного направления и одинаковой частоты амплитуда результирующего колебания определяется соотношением:
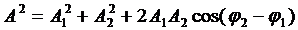 ,
,
где 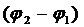 – разность фаз складываемых колебаний.
– разность фаз складываемых колебаний.






