В задаче принято допущение, что температура конденсации не зависит от режима работы холодильной установки и имеет определенное фиксированное значение, т.е. рассматривается не вся установка в целом, а лишь совместная работа части оборудования: компрессоров и воздухоохладителей.
Уравнение теплового баланса для камеры хранения, работающей в стационарном режиме, имеют вид:
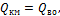
| (5.1) |
где  – холодопроизводительность компрессора, Вт;
– холодопроизводительность компрессора, Вт; 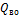 – тепловой поток, передаваемый в воздухоохладителе, Вт.
– тепловой поток, передаваемый в воздухоохладителе, Вт.
Считается, что при включении или выключении из работы воздухоохладителей происходит автоматическое изменение холодопроизводительности компрессора с целью поддержания при прежнем значении 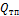 заданного значения температуры помещения, но, естественно, уже при другой температуре кипения холодильного агента.
заданного значения температуры помещения, но, естественно, уже при другой температуре кипения холодильного агента.
Система уравнений, позволяющая определить стабилизированное значение температуры кипения в зависимости от числа включенных в работу воздухоохладителей в нашем случае, с учетом допущения, что температура воздуха на входе в воздухоохладители равна температуре помещения, запишется следующим образом:

| (5.2) |
где 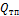 – теплопритоки в помещение (холодильную камеру), не зависящие от числа включенных в работу воздухоохладителей, Вт;
– теплопритоки в помещение (холодильную камеру), не зависящие от числа включенных в работу воздухоохладителей, Вт; 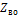 – число включенных в работу воздухоохладителей;
– число включенных в работу воздухоохладителей;  – тепловой эквивалент работы воздухоохладителя, Вт;
– тепловой эквивалент работы воздухоохладителя, Вт; 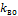 – коэффициент теплопередачи воздухоохладителей, Вт/(м2 К);
– коэффициент теплопередачи воздухоохладителей, Вт/(м2 К);  – поверхность теплопередачи воздухоохладителя, м2;
– поверхность теплопередачи воздухоохладителя, м2;  – температура помещения, оС;
– температура помещения, оС;  – температура воздуха на выходе из воздухоохладителя, оС;
– температура воздуха на выходе из воздухоохладителя, оС;  – объемный расход воздуха, проходящего через воздухоохладитель, м3/с;
– объемный расход воздуха, проходящего через воздухоохладитель, м3/с; 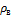 – плотность воздуха, кг/м3;
– плотность воздуха, кг/м3;  – удельная массовая изобарная теплоёмкость воздуха, Дж/(кг К).
– удельная массовая изобарная теплоёмкость воздуха, Дж/(кг К).
Решением приведенной выше системы уравнений является следующее выражение для температуры кипения:
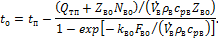
| (5.3) |
Суммарный расход электроэнергии на привод компрессора и воздухоохладителей с учетом равенства (5.1):

| (5.4) |
где  – удельная холодопроизводительность компрессора:
– удельная холодопроизводительность компрессора:
 . .
| (5.5) |
Зависимости холодопроизводительности компрессора  и его эффективной мощности
и его эффективной мощности  от температур кипения
от температур кипения  и конденсации
и конденсации  получают при испытаниях компрессора. Приведённая в (5.5) эмпирическая зависимость соответствует компрессору конкретной марки.
получают при испытаниях компрессора. Приведённая в (5.5) эмпирическая зависимость соответствует компрессору конкретной марки.
Таблица 5
Исходные данные
| Наименование параметра | Первая цифра варианта | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
 , оС , оС
| 0 | 0 | 0 | -2 | -2 | -2 | -10 | -10 | -10 | -10 |
 , оС , оС
| 25 | 25 | 23 | 23 | 21 | 21 | 20 | 20 | 20 | 20 |
| Наименование параметра | Вторая цифра варианта | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
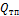 , кВт , кВт
| 500 | 700 | 600 | 650 | 600 | 400 | 700 | 500 | 550 | 750 |
| Тип воздухоохладителя | ВОП-50 ВОП-150 | ВОП-100 ВОП-230 | ВОП-75 ВОП-50 | ВОП-75 ВОП-230 | ВОП-150 ВОП-230 | ВОП-50 ВОП-75 | ВОП-50 ВОП-100 | ВОП-50 ВОП-75 | ВОП-150 ВОП-230 | ВОП-100 ВОП-150 |
Ограничения на вводимые параметры:
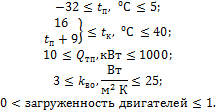
Вопросы для самопроверки
1. Из каких основных уравнений состоит математическая модель совместной работы компрессоров и воздухоохладителей в составе холодильной установки?
2. Какое допущение положено в основу математической модели совместной работы компрессоров и воздухоохладителей в составе холодильной установки?
3. Напишите уравнение теплового баланса для воздухоохладителя.
4. Сформулируйте задачу оптимизации числа включенных в работу воздухоохладителей.
5. Объясните, почему соответствующее оптимальному числу включенных воздухоохладителей значение перепада температур  может, для данных конкретных условий, отличаться от рекомендуемых в теории средних перепадов температур (8 – 12 оС)?
может, для данных конкретных условий, отличаться от рекомендуемых в теории средних перепадов температур (8 – 12 оС)?
6. Напишите уравнение теплового баланса для охлаждаемого помещения, работающего в стационарном режиме.
7. Какими уравнениями описывается в данной математической модели работа компрессора? Можно ли описать работу компрессора в данной задаче другими уравнениями, если можно, то опишите их.
ЛАБОРАТОРНАЯ РАБОТА №6






