ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
| Дальневосточный государственный технический рыбохозяйственный университет |
С.А. Остренко
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ФИЗИЧЕСКИХ ПРОЦЕССОВ В ХОЛОДИЛЬНОЙ ТЕХНИКЕ
Методические указания по выполнению лабораторных работ и организации самостоятельной работы студентов направления 16.03.03 «Холодильная, криогенная техника и системы жизнеобеспечения» всех форм обучения
Владивосток
Дальрыбвтуз
2016
УДК 621.565:519.711
ББК 31.392
О-76
Утверждено редакционно-издательским советом Дальневосточного государственного технического рыбохозяйственного университета
Автор – С.А. Остренко
Рецензент – В.П. Шайдуллина, канд. техн. наук, доцент
© Дальневосточный государственный
технический рыбохозяйственный
университет, 2016
ЛАБОРАТОРНАЯ РАБОТА №1
Моделирование тепловой изоляции холодного трубопровода при отсутствии конденсации влаги на его поверхности
Цель работы. Разработать математическую модель тепловой изоляции трубопроводов холодильной установки с условием отсутствия конденсации влаги на её поверхности. Приобрести навыки анализа влияния независимых переменных математической модели на минимальную толщину изоляции, при которой отсутствует конденсация влаги на её поверхности.
Задание:
1. Провести анализ процессов, протекающих при переносе теплоты через тепловую изоляцию трубопровода. Выделить факторы, оказывающие влияние на конденсацию пара из влажного воздуха помещения. Составить замкнутую систему уравнений процессов, протекающих в рассматриваемой задаче (математическую модель), и продумать алгоритм её решения. Реализовать математическую модель тепловой изоляции трубопровода в Excel.
2. Проанализировать влияние нижеперечисленных параметров на минимальную требуемую толщину изоляции холодного трубопровода, при которой отсутствует конденсация влаги на его поверхности:
× температуры наружного воздуха t в;
× относительной влажности воздуха помещения j;
× температуры среды внутри трубопровода t хн;
× коэффициента теплоотдачи к холодной среде a вн;
× коэффициента теплоотдачи к окружающей среде (воздуху) a нар.
3. Построить графики зависимостей толщины изоляции В из от выбранного параметра.
4. По полученным результатам сделать выводы. Выводы должны содержать описание характера влияния исследуемого параметра на минимальную требуемую толщину изоляции холодного трубопровода и объяснение этого влияния.
Краткое описание математической модели
Математическая постановка задачи приведена в [2].
Термин "холодный" означает, что температура движущейся по трубопроводу среды ниже температуры окружающей среды.
Условие недопущения конденсации влаги на поверхности:
 ,
| (1.1) |
где 
– температура поверхности изоляции, oC; 
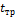– температура точки росы при температуре воздуха в помещении 
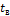и его относительной влажности 
.
При постоянной температуре среды внутри трубопровода температура на поверхности изоляции тем выше, чем больше толщина изоляции. Существует такая минимальная толщина изоляции, при которой температура поверхности достигает точки росы, и начинает выполняться условие отсутствия конденсации влаги.
Для определения требуемого наружного диаметра изоляции необходимо выразить температуру её поверхности в виде зависимости от толщины изоляционного слоя.
Линейная плотность теплового потока через изоляцию определяется по уравнению теплопередачи через цилиндрическую поверхность. В стационарном режиме, пренебрегая термическим сопротивлением металлической стенки трубы (из-за его малости), это уравнение примет вид:
| (1.2) |
где 
и 
– внутренний диаметр трубопровода и наружный диаметр изоляции, соответственно, м; 
– наружный диаметр неизолированной трубы, м; 
– коэффициент теплопроводности материала изоляции, Вт/(м∙К).
В стационарных условиях эту же линейную плотность теплового потока можно определить по уравнению теплоотдачи от наружной поверхности изоляции, температура которой равна 
, к окружающей среде (воздуху):
| (1.3) |
Приравняв обе зависимости и заменив температуру наружной поверхности изоляции на температуру точки росы 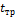(в момент начала конденсации пара на поверхности изоляции они равны),можно численно решить получающееся трансцендентное уравнение относительно :
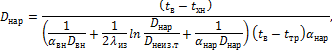
| (1.4) |
и определить требуемую толщину изоляции:
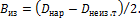
| (1.5) |
Температура точки росы определяется из условия, что в процессе охлаждения ненасыщенного влажного воздуха (
до насыщенного его состояния (
), которому соответствует 
влагосодержание d не меняется. Поэтому, рассчитав влагосодержание по параметрам влажного воздуха в помещении 
, используем полученное значение для определения давления насыщенного пара при температуре точки росы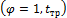 
.
 .
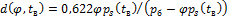| (1.6) |
| (1.7) |
откуда
| (1.8) |
Здесь 
– давление влажного воздуха в помещении, которое обычно равно барометрическому давлению; 
− давление насыщения водяного пара при температуре воздуха в помещении; 
− давление насыщения водяного пара при температуре точки росы.
Поскольку в состоянии насыщения температура и давление взаимосвязаны, то найденному значению давления насыщения однозначно соответствует температура насыщения, которая соответствует искомой температуре точки росы.
При любой большей толщине изоляции (например, полученной после увеличения рассчитанного значения до величины, кратной толщине стандартного слоя изоляции), конденсация влаги на поверхности изоляции отсутствует.
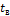Математический анализ полученных уравнений подтверждает физически обоснованное положение: при влажности воздуха = 100%, что означает равенство температур и 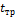,предотвратить конденсацию влаги на поверхности изоляции невозможно, поскольку потребуется бесконечно большой наружный диаметр изоляции.
Ограничения на вводимые параметры:
