Правило Лопиталя
Теорема. Пусть функции  и
и  :
:
1) дифференцируемы в некоторой окрестности точки  (
( - число или
- число или  ), за исключением, может быть, самой точки
), за исключением, может быть, самой точки  2) являются одновременно либо бесконечно малыми, либо бесконечно большими при
2) являются одновременно либо бесконечно малыми, либо бесконечно большими при  3)
3)  в указанной окрестности. Если существует конечный предел
в указанной окрестности. Если существует конечный предел  (
( конечное либо
конечное либо  ), то существует и
), то существует и 
Данное утверждение справедливо и для одностороннего предела, когда  либо
либо 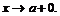
Пример 1. Найти 
Имеем неопределённость вида  , условия теоремы выполнены. Поэтому согласно правилу Лопиталя получим:
, условия теоремы выполнены. Поэтому согласно правилу Лопиталя получим:
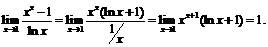
Пример 2. Найти 

Раскроем неопределённость вида  по правилу Лопиталя:
по правилу Лопиталя:

Иногда правило Лопиталя приходится применять последовательно несколько раз, чтобы избавиться от неопределённости.
Пример 3. Найти 
Для неопределённости  по теореме Лопиталя получим:
по теореме Лопиталя получим:

Применяя теорему Лопиталя, можно использовать известные асимптотические равенства, поскольку это иногда существенно упрощает выкладки.
Пример 4. Найти 

Учитывая, что при 
 будем иметь:
будем иметь:
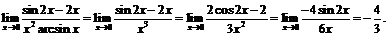
Пример 5. Найти 
Применяя к неопределённости вида  правило Лопиталя последовательно два раза, получим:
правило Лопиталя последовательно два раза, получим:



В примерах 6-9 требуется раскрыть неопределённость вида 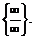
Пример 6. Найти 
Используя эквивалентность  при
при  и теорему Лопиталя, получим:
и теорему Лопиталя, получим:
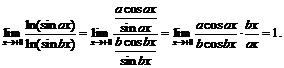
Пример 7. Найти 
Применяя правило Лопиталя два раза, будем иметь:


Пример 8. Найти 
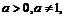

Для 
 такое, что
такое, что  а тогда
а тогда  Покажем, что для
Покажем, что для 
 , применив правило Лопиталя
, применив правило Лопиталя  раз:
раз: 
Согласно принципу двустороннего ограничения:
 для
для 
Пример 9. Найти 
По теореме о пределе произведения получим:
 а к пределу
а к пределу  применим правило Лопиталя:
применим правило Лопиталя:
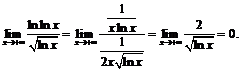
Тогда 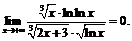
Для раскрытия неопределённости вида  необходимо сначала преобразовать выражение, чтобы получить неопределённость
необходимо сначала преобразовать выражение, чтобы получить неопределённость  или
или  .
.
Пример 10. Найти 
C помощью элементарных преобразований сведём неопределённость вида 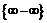 к неопределённости
к неопределённости  , воспользуемся асимптотическим равенством
, воспользуемся асимптотическим равенством  при
при  и применим правило Лопиталя:
и применим правило Лопиталя:

Пример 11. Найти 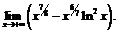
Преобразуем данную функцию:

Рассмотрим  и применим правило Лопиталя последовательно два раза:
и применим правило Лопиталя последовательно два раза:
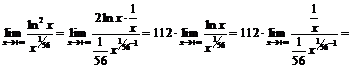
 Следовательно,
Следовательно,
 а тогда
а тогда 
В примерах 12-14 требуется раскрыть неопределённость вида 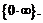
Пример 12. Найти 
Сведя неопределённость  к неопределённости
к неопределённости  , применим правило Лопиталя последовательно два раза:
, применим правило Лопиталя последовательно два раза: 

Пример 13. Найти 


Пример 14. Найти 
Сделаем замену переменной  если
если  то
то  Тогда
Тогда  .
.
Применяя к полученному пределу правило Лопиталя, будем иметь: 

В примерах 15-20 для раскрытия неопределённостей вида 
 и
и  воспользуемся логарифмическим тождеством
воспользуемся логарифмическим тождеством  и сведём вычисление предела к раскрытию неопределённости
и сведём вычисление предела к раскрытию неопределённости 
Пример 15. Найти 
Применяя логарифмическое тождество, придём к вычислению следующего предела:
 для которого после двукратного применения правила Лопиталя получим:
для которого после двукратного применения правила Лопиталя получим:
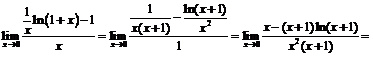

Тогда 
Пример 16. Найти 
C помощью логарифмического тождества преобразуем неопределённость  к неопределённости вида
к неопределённости вида  , к которой применим затем правило Лопиталя и следствие из 2-го замечательного предела:
, к которой применим затем правило Лопиталя и следствие из 2-го замечательного предела:

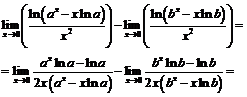
 Тогда
Тогда 
Пример 17. Найти 
С использованием результата примера 13 получим:

Пример 18. Найти 
Полагая  получим:
получим: 
Так как  и
и  при
при  то согласно примеру 13 будем иметь:
то согласно примеру 13 будем иметь: 
Пример 19. Найти 
 Согласно правилу Лопиталя:
Согласно правилу Лопиталя:

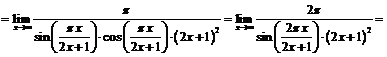


Следовательно, 
Пример 20. Найти 
 Тогда по правилу Лопиталя и с использованием примера 8 будем иметь:
Тогда по правилу Лопиталя и с использованием примера 8 будем иметь:
 .
.
Поэтому 
Пример 21. Найти 
Пусть сначала  Если
Если 
 то функции
то функции 
 и
и  есть бесконечно малые при
есть бесконечно малые при  а следовательно,
а следовательно,  Если же
Если же  а
а  - любое, то
- любое, то  откуда следует, что:
откуда следует, что:
 , а
, а 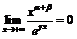 (пример 8). Согласно принципу двустороннего ограничения
(пример 8). Согласно принципу двустороннего ограничения  . Итак, доказано: при
. Итак, доказано: при  и
и 
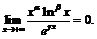
Пусть теперь  Так как по доказанному выше
Так как по доказанному выше  то обратная величина является бесконечно большой при
то обратная величина является бесконечно большой при 
 для
для 
Если же  то имеем:
то имеем:  Сделаем замену
Сделаем замену  будем иметь:
будем иметь:  Тогда:
Тогда:
1)  при
при  и
и  и при
и при  и
и 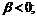
2)  при
при  и
и  и при
и при  и
и 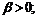
3)  если
если 
Окончательно, предел равен нулю, если  (
( ) либо
) либо 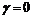 (
(
 или
или 
 );
);
предел равен  если
если  (
( ) либо
) либо 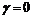 (
(
 или
или 
 ); предел равен 1, если
); предел равен 1, если 
Применение правила Лопиталя не всегда возможно, поэтому надо внимательно следить за выполнением условий теоремы.
Пример 22. Объяснить, почему следующие пределы не могут быть найдены по правилу Лопиталя и найти их, если они существуют: 1)  ; 2)
; 2)  .
.
Правило Лопиталя в обоих случаях неприменимо, так как предел отношения производных не существует, однако с использованием леммы о бесконечно малых легко получить, что 1) 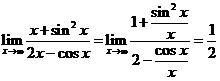 ;
;
2)  .
.
Пример 23. Исследовать возможность применения правила Лопиталя к следующему пределу:  .
.
Условия теоремы не выполнены, ибо производные  и
и  обращаются в нуль одновременно в любой окрестности точки
обращаются в нуль одновременно в любой окрестности точки  , если
, если 
 , поэтому правило Лопиталя использовать нельзя. Отметим, что данный предел не существует, что легко получить по определению Гейне:
, поэтому правило Лопиталя использовать нельзя. Отметим, что данный предел не существует, что легко получить по определению Гейне:
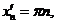

 , если
, если  , то и
, то и 
 ; при этом
; при этом  , а
, а  при
при  .
.
Упражнения для самостоятельной работы
Определить значения следующих выражений:
1.  2.
2.  3.
3. 
4. 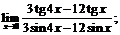 5.
5.  6.
6. 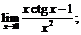
7.  8.
8. 
9.  10.
10. 

11.  12.
12. 
13.  14.
14. 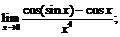 15.
15. 
16.  17.
17. 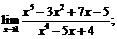 18.
18. 
19.  20.
20. 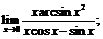
21.  22.
22. 
23.  24.
24. 
25.  26.
26. 

27.  28.
28. 

29. 

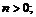 30.
30.  31.
31. 
32. 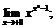 33.
33.  34.
34.  35.
35. 
36.  37.
37.  38.
38. 
39. 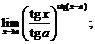 40.
40.  41.
41. 
42.  43.
43. 
44.  45.
45.  46.
46. 
47. 

48.  49.
49. 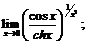
50.  51.
51.  52.
52. 
53. 
54. 
55.  56.
56. 
57.  58.
58. 
59. Показать, что следующие пределы не могут быть вычислены по правилу Лопиталя, и найти эти пределы:
1)  ; 2)
; 2) 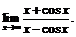
60. Исследовать возможность применения правила Лопиталя к следующему пределу:  .
.
Формула Тейлора
Локальная формула Тейлора или формула Тейлора с остаточным членом в форме Пеано.
Пусть функция  , определённая в окрестности точки
, определённая в окрестности точки 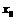 , имеет в этой окрестности производные до
, имеет в этой окрестности производные до  -го порядка включительно, а в точке
-го порядка включительно, а в точке 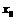 существует
существует  . Тогда справедливо следующее представление:
. Тогда справедливо следующее представление:



Многочлен  называется многочленом Тейлора функции
называется многочленом Тейлора функции  в точке
в точке 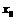 , а функция
, а функция  -
-  -тым остаточным членом.
-тым остаточным членом.
Формула Тейлора на промежутке.
Если на отрезке с концами 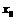 и
и 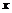 функция
функция  непрерывна вместе со своими производными до
непрерывна вместе со своими производными до  -го порядка включительно, а во внутренних точках она имеет
-го порядка включительно, а во внутренних точках она имеет  -ю производную, то какова бы ни была функция
-ю производную, то какова бы ни была функция  непрерывная на данном отрезке и имеющая отличную от нуля производную в его внутренних точках, найдётся точка
непрерывная на данном отрезке и имеющая отличную от нуля производную в его внутренних точках, найдётся точка  лежащая между
лежащая между 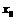 и
и 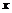 и такая, что
и такая, что

Если при выполненных условиях теоремы
1) 

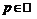 - произвольно, то остаточный член в формуле Тейлора представим в виде Шлемильха-Роша:
- произвольно, то остаточный член в формуле Тейлора представим в виде Шлемильха-Роша:

2)  то остаточный член в формуле Тейлора представим в форме Лагранжа:
то остаточный член в формуле Тейлора представим в форме Лагранжа:

3)  то остаточный член в формуле Тейлора представим в форме Коши:
то остаточный член в формуле Тейлора представим в форме Коши:

Если  то формула Тейлора принимает вид:
то формула Тейлора принимает вид:
 и называется формулой Маклорена.
и называется формулой Маклорена.
Справедливы пять важных разложений:
1. 
2. 
3. 
4. 
5. 
В примерах 1-14 разложить функцию  по формуле Маклорена до
по формуле Маклорена до 
Пример 1. 
Пользуясь разложением 1, получим:
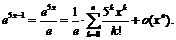
Пример 2. 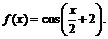
Так как  т.е.
т.е.  то разложение по формуле Тейлора будет иметь следующий вид:
то разложение по формуле Тейлора будет иметь следующий вид:

Пример 3. 
Учитывая, что  и используя разложение 1, получим:
и используя разложение 1, получим:

Пример 4. 
Так как  то с использованием разложения 5 будем иметь:
то с использованием разложения 5 будем иметь:

Пример 5. 
Из разложения 4 следует: 
Поэтому 



Пример 6. 
Преобразовав подкоренное выражение, используем затем разложение 5:

 где
где
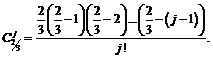
Пример 7. 
После преобразований применим разложение 4:




Учитывая, что  и
и  , будем иметь:
, будем иметь:

Пример 8. 
Разделив числитель на знаменатель, представим  в виде:
в виде:

Тогда 


Пример 9. 
Так как 
 то используя разложение 2, будем иметь:
то используя разложение 2, будем иметь:


Пример 10. 
Учитывая, что  а
а

 получим:
получим:


Пример 11. 
Используя формулу 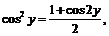 преобразуем функцию:
преобразуем функцию: 

Применяя разложение 3, будем иметь:

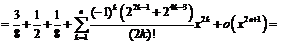

Пример 12. 
Преобразуя функцию с помощью формул понижения степени 
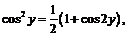 получим:
получим:  откуда с использованием разложения 3 будем иметь:
откуда с использованием разложения 3 будем иметь:
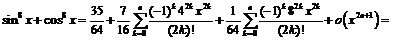

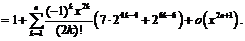
Пример 13. 
Представим  в виде суммы дробей:
в виде суммы дробей:



Пример 14. 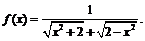
Преобразуем функцию: 

Воспользуемся разложением 5, введя для краткости следующее общепринятое обозначение:


 тогда
тогда  Следовательно,
Следовательно,


 Заменяя переменную
Заменяя переменную  окончательно получим:
окончательно получим: 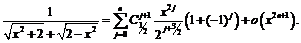
Если функция  имеет вид:
имеет вид:  и известны разложения функций
и известны разложения функций  и
и  по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  до
до 
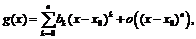
 причём
причём 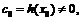 то для нахождения разложения функции
то для нахождения разложения функции  применим метод неопределённых коэффициентов. Пусть искомое разложение имеет вид:
применим метод неопределённых коэффициентов. Пусть искомое разложение имеет вид:
 тогда, так как
тогда, так как  или
или

 то приравнивая в последнем равенстве коэффициенты при одинаковых степенях
то приравнивая в последнем равенстве коэффициенты при одинаковых степенях  в правой и левой частях, получим систему алгебраических уравнений для определения
в правой и левой частях, получим систему алгебраических уравнений для определения 


Пример 15. Применяя метод неопределённых коэффициентов, разложить по формуле Маклорена функцию  до
до 
Учитывая, что функция  нечётная и
нечётная и  т.е.
т.е.  будем иметь:
будем иметь: 
Применяя разложения 2 и 3 и формулу  получим:
получим:

 Приравнивая коэффициенты при
Приравнивая коэффициенты при 
 и
и  находим:
находим:





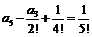






Итак, 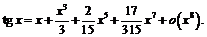
Если  - сложная функция и известны разложения функций
- сложная функция и известны разложения функций  и
и  по формуле Тейлора:
по формуле Тейлора:




то для нахождения коэффициентов разложения

нужно в формулу  подставить
подставить  заменить её разложением
заменить её разложением  и произвести арифметические действия, сохраняя лишь члены вида
и произвести арифметические действия, сохраняя лишь члены вида  где
где 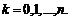
Пример 16.  Разложить по формуле Маклорена до
Разложить по формуле Маклорена до  функцию
функцию 
 Используя разложения 2 и 4, получим:
Используя разложения 2 и 4, получим:
 Для
Для  имеем:
имеем:  поэтому, оставляя лишь члены вида
поэтому, оставляя лишь члены вида 
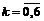 , будем иметь:
, будем иметь:




Если требуется разложить функцию  по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  то, сделав замену
то, сделав замену  мы получим функцию
мы получим функцию  которую необходимо разложить по формуле Маклорена.
которую необходимо разложить по формуле Маклорена.
Пример 17. Разложить по формуле Тейлора в окрестности точки 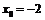 функцию
функцию  до
до 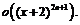
Пусть 
 тогда
тогда 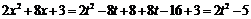 и
и 

Пример 18. Разложить по формуле Тейлора в окрестности точки  функцию
функцию  до
до 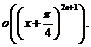
Пусть 

 тогда
тогда

 откуда следует:
откуда следует:
 Пример 19. Разложить по формуле Тейлора в окрестности точки
Пример 19. Разложить по формуле Тейлора в окрестности точки  до
до  функцию
функцию 
Обозначим 
 тогда
тогда 
и 
Используя разложение 5, получим:

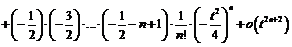 , откуда
, откуда
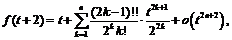

Если известно разложение по формуле Тейлора в окрестности точки 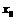 до
до  производной
производной  функции
функции 
 где
где  то существует
то существует  и функцию
и функцию  можно представить в виде:
можно представить в виде:

 где
где  Но
Но  поэтому
поэтому  Следовательно,
Следовательно,
 ,
, 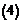
 - коэффициенты разложения по формуле Тейлора для функции
- коэффициенты разложения по формуле Тейлора для функции 
Пример 20. Разложить по формуле Маклорена до  функций: 1)
функций: 1)  2)
2) 
3) 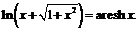
1)  и используя разложение 5, получим:
и используя разложение 5, получим:



Согласно формуле 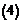 будем иметь:
будем иметь:

2) 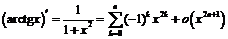 (легко получить с использованием формулы для геометрической прогрессии). Тогда по формуле
(легко получить с использованием формулы для геометрической прогрессии). Тогда по формуле 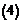 можно записать:
можно записать:

3) 
откуда по формуле 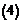 находим:
находим:

Пример 21. Разложить по формуле Маклорена до  функцию
функцию  Число
Число  выбрать наибольшим.
выбрать наибольшим.
Рассмотрим функцию 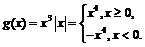
Найдём её производные. При 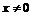
 При
При  по определению производной находим:
по определению производной находим:

Таким образом, первая производная существует при всех  причём
причём  Аналогично для второй производной получаем:
Аналогично для второй производной получаем: 
 т.е. вторая производная существует при всех
т.е. вторая производная существует при всех 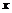 и равна
и равна  Для третьей производной имеем:
Для третьей производной имеем:

 Следовательно,
Следовательно,  Так как функция
Так как функция 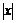 не дифференцируема в точке
не дифференцируема в точке  то рассматриваемая функция
то рассматриваемая функция  не имеет в точке
не имеет в точке  четвёртой производной (и производных порядка выше четвёртого), а обладает в этой точке производными до третьего порядка включительно. Поэтому разложение по формуле Маклорена до
четвёртой производной (и производных порядка выше четвёртого), а обладает в этой точке производными до третьего порядка включительно. Поэтому разложение по формуле Маклорена до  при
при 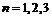 выглядит следующим образом:
выглядит следующим образом:


 а разложение
а разложение  по формуле Маклорена до
по формуле Маклорена до  не существует. Итак,
не существует. Итак, 
Возвращаясь к функции  и используя разложение 2 для
и используя разложение 2 для  будем иметь:
будем иметь:
 поэтому
поэтому 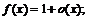
 так как
так как

Пример 22. Оценить с помощью формулы Тейлора абсолютную погрешность приближённой формулы:


По формуле Тейлора с остаточным членом в форме Лагранжа:

где 
Пример 23. Написать многочлен Тейлора порядка  и оценить разность этого многочлена и функции на указанном отрезке, принимая в качестве
и оценить разность этого многочлена и функции на указанном отрезке, принимая в качестве 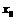 середину этого отрезка:
середину этого отрезка:  на
на 

По условию  Находим производные функции:
Находим производные функции:








