Предел функции в точке и на бесконечности. Теоремы о пределах
Понятие предела функции
Пусть у=f(х) − функция с областью определения Х, причем а− некоторое число.
Число b называется пределом функции f(х) в предельной точке а, если значения функции неограниченно приближаются к число b, при всех значениях х, достаточно близких к а. Предел функции в точке а обозначается
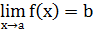
Если область определении X функции f(х) содержит сколь угодно большие по абсолютной величине положительные (отрицательные) значения х, то в этом случае можно рассматривать предел функции на бесконечности.
Число b называетсяпределом функцииf(х)при х→+∞ если для любой последовательности 
соответствующая последовательность значений функции сходится к числу b:
=b
Таким образом, число b называетсяпределом функции f(х) при х→∞, если значения функции неограниченно приближаются к числу b (то есть 
), когда аргумент х, изменяясь, принимает сколь угодно большие по абсолютной величине значения.
Свойства предела функции
| 1. Функция 2. 3. 4. 5. Если пределы функций у=f(x) и y=g(x) существуют, то 6. 7. 8. 9. |
при 
имеет единственный предел.
=∞, если 
, если g(x)≠010. 
=0, если f(x)=0, g(x)≠0 
| Функция у=f(x) называется бесконечно малой при х→а, |
если f(x)=0.
Функция у=f(x) называется бесконечно большой при х→а, если 
f(x)=∞.
Пример 1.Вычислить предел: lim (2x3-4x2+5)
x→2
Решение.lim (2x3-4x2+5)=2 ∙23-4∙ 22+5=5
x →2
Пример 2. Вычислить предел: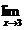 
Решение.Предел знаменателя равен нулю: 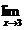(2х-6)=2∙3-6=0, поэтому теорему о пределе частного применить нельзя. Т.к. 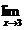(2х-6)=0, то 2х-6 при х→2 величина бесконечно малая, тогда 
бесконечно большая. Поэтому при х→2 
величина бесконечно малая, т.е. 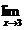=0
Если при подстановке в функцию предельного значения аргумента в функцию получится неопределенность вида 
, 
, 0∙∞, ∞−∞, 00, ∞0, 10, то используются специальные приёмы, которые называют раскрытием неопределённость.
Неопределенность 
1. Чтобы раскрыть неопределенность вида , заданную отношением двух многочленов, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени.
2. Для раскрытия неопределенности вида , заданную отношением иррациональных функций, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени с учетом степеней корней.
Неопределенность 
1. Чтобы раскрыть неопределенность вида , необходимо предварительно сократить дробь (разложив на множители по формуле 
или
.
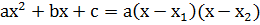2. Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель иррациональны, следует избавиться от иррациональности, умножив и числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения и сократить дробь. [2]
Пример 3.Вычислить предел: 
Решение. При непосредственной подстановке получается неопределённость 
.
Для раскрытия неопределённости необходимо предварительно сократить дробь (разложив на множители)
= 
= 
= 
=- 
Пример 4. Вычислить предел: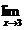 
Решение. При непосредственной подстановке получается неопределённость .
Для раскрытия неопределённости необходимо, предварительно решить квадратное уравнение и разложить на множители квадратный трёхчлен ах2+bx+c=a(x-x1)(x-x2)
= 
= 
= 
= 
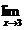
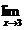
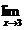
Пример 5.Вычислить предел: 
Решение. При непосредственной подстановке получается неопределенность 
, поэтому вынесем за скобку степень с наивысшем показателем, сократим их в числителе и знаменателе.
Пример 6. Найти 
Решение. Предел знаменателя равен 0, предел числителя также равен 0. Получим неопределенность вида 
к тому же под знаком предела имеем иррациональность. В этом случае для раскрытия неопределенности необходимо тождественно преобразовать заданное под знаком предела выражение, умножая числитель и знаменатель на сопряженный сомножитель, упростить дробь и перейти к пределу:
I и II замечательные пределы.