Эквиваленция обозначается значком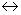 
и читается «тогда и только тогда»
Наверное, многие догадываются, что это за операция:
Эквиваленцией высказываний 
и 
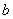называют высказывание 
, которое истинно в том и только том случае, когда высказывания и 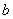истинны или ложны одновременно:
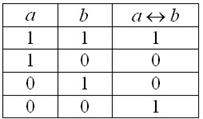
Данная операция естественным образом выражается формулой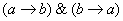 
– «из а следует бэ и из бэ следует а».
Предположим, что Петя вышел на финишную черту сессии, и ему осталось сдать 3 экзамена:
– три экзамена сданы;
– сессия успешно завершена.
Очевидно, что при описанных выше обстоятельствах эти высказывания эквиваленты:
– сессия успешно завершена тогда и только тогда, когда сдано 3 экзамена.
Перед вами пример необходимого и достаточного условия: для того чтобы завершить сессию успешно Пете необходимо сдать 3 экзамена (в противном случае сессия будет не сдана) и в то же самое время этого достаточно (т.к. больше ничего делать не нужно).
Особенность эквиваленции состоит в том, что имеет место либо и то и другое, либо ничего, например:
Петя занимается штангой тогда и только тогда, когда Маша танцует на столе
Это значит, что либо Петя занимается штангой и Маша танцует на столе, либо они оба лежат на диване Пётр, ты заслужил! =) Такие вот дружные Петя и Маша. Теперь вроде бы похожая фраза без «тогда и только тогда»:
Петя занимается штангой, когда Маша танцует на столе
Но смысл несколько поменялся: здесь можно предположить, что Петя, бывает, тягает штангу и без Маши, и другой стороны, Маше «до лампочки», качается ли во время её танца Петя.
Вот в чём сила необходимого и достаточного условия! – оно объединяет и дисциплинирует =)
…хотел я для прикола распределить роли наоборот, но затем передумал… всё-таки нельзя такое пропагандировать =)
К слову, о дисциплине – рациональный подход как раз и предполагает необходимость и достаточность – когда человек для достижения какой-либо цели делает ровно столько, сколько нужно, и не больше. Это, конечно, бывает скучно в обычной жизни, но всячески приветствуется в математических рассуждениях, которые нас уже заждались:
Треугольник является равносторонним тогда и только тогда, когда у него равные углы
Высказывания 
– треугольник равносторонний и 
– у него равные углы можно соотнести эквиваленцией 
, но на практике мы почти всегда связываем их обоюдоострым значком логического следствия 
, который тоже читается «тогда и только тогда». Отличие от эквиваленции такое же:
– когда мы утверждаем, что 
, то изначально полагаем высказывание истиной (и никак не ложью). И наоборот, запись 
подразумевает безусловную истинность посылки .
И в заключение первой части урока вспомним знаменитую теорему, которую я переформулирую «по-взрослому»:
Для того, чтобы треугольник был прямоугольным необходимо и достаточно, чтобы квадрат одной из его сторон равнялся сумме квадратов двух других сторон: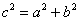 
Напоминаю, что сторона 
называется гипотенузой (бОльшая сторона, лежащая напротив угла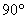 
), а стороны 
– катетами.
Перепишем теорему в сокращённой записи:
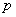– треугольник прямоугольный 
– выполнено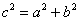
Доказательство «теорем такого типа» состоит из 2 частей, у которых тоже есть стандартные названия (наверное, неоднократно сталкивались):
1) Необходимость (условия ):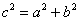
– иными словами, тут нужно доказать, что для того, чтобы треугольник был прямоугольным, необходимо выполнение равенства .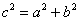
Данный пункт – это собственно и есть теорема Пифагора, формулировка которой нам знакома ещё со школы: «Если треугольник прямоугольный, то ».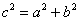
2) На втором шаге обосновывается достаточность:
– здесь надо доказать, что справедливость равенства 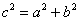достаточна для того, чтобы треугольник был прямоугольным.
Учащихся опять же такими словами не запугивают, и второй пункт формулируют в виде обратной теоремы Пифагора: «Если 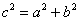, то треугольник прямоугольный».
Связей по схеме «тогда и только тогда» в математике очень много, и я только что привёл стандартную схему их доказательства. И, конечно же, всегда анализируйте, что означают «необходимо», «достаточно», «необходимо и достаточно» в том или ином случае.
Следует отметить, что теорему можно рассмотреть с точки зрения логической операции 
, но вот запись 
(как и обратная запись 
) становится нелегальной! Почему? Пусть 
– треугольник не прямоугольный, 
– равенство 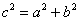выполнено. Но тогда по импликационной таблице получаем 
, что не соответствует действительности!
Но зато записи 
совершенно законны, поскольку логическое следствие отталкивается исключительно от истины!
Жду вас во второй части нашего увлекательного урока, где мы познакомимся с основными логическими формулами и законами, а также порешаем практические задачи. Для решения задач потребуется пять табличек с этой страницы, поэтому я рекомендую сразу переписать их на листок – чтобы они были перед глазами.
Кроме того, я открою вам секрет успешного изучения математической логики;)
