Угол между векторами а и можно также обозначать.

Свойства углов.

1⁰. Для любых двух ненулевых векторов угол между ними определён.

Из формулы (45) следует, что Следовательно, j существует.

2⁰. Если a ¹ 0, b ¹ 0, то .

Определение 48. Два ненулевых вектора называются ортогональными, если их скалярное произведение равно нулю.

Ортогональные векторы обозначаются а ^ в.

3⁰. Если а ^ в, a ¹ 0, b ¹ 0, то (a а)^ (b в).

4⁰. Если а ^ в и а ^ с и в + с ¹ 0, то а ^ (в + с).

Определение 50. Множество всех векторов пространства Е_n, ортогональных вектору а, к которому добавлен нулевой вектор, называется ортогональным дополнением вектора а.

5⁰. Ортогональное дополнение к вектору а является (n – 1)-мерным евклидовым подпространством в Е_n.

Доказательство.

Из свойств 3⁰ и 4⁰ следует, что рассматриваемое множество L является линейным подпространством в Е_n. Так как в Е_n определено скалярное произведение, то оно определено и в ортогональном дополнении, следовательно, L является евклидовым подпространством. Кроме того, с Î L Û (а, с) = 0 (*). Зафиксируем в Е_n базис. Пусть а = (а₁, а₂, …, а_n), с = (х₁, х₂, …, х_n). Тогда с Î L Û а^Т ×Г ×х = 0 (**). Уравнение (**) есть линейное однородное уравнение с n неизвестными. Фундаментальная система его решений состоит из (n – 1) решения. Следовательно, пространство решений уравнения (**) является (n – 1)-мерным.

Пусть Е_к – подпространство пространства Е_n. Обозначим Е множество, состоящее из нулевого вектора и всех векторов, ортогональных любому ненулевому вектору из Е_к. Иными словами с Î Е Û (с, а) = 0 для всех а Î Е_к. Пространство Е ортогональным дополнением к пространству Е_к.

6⁰. Ортогональное дополнение Е является (n – к)-мерным евклидовым подпространством в пространстве Е_n.

Доказательство аналогично доказательству свойства 5⁰.

7⁰. Е Ç Е_к = { 0 }.

8⁰. Любые два ортогональных вектора линейно независимы.

Доказательство. Пусть а ^ в. По определению эти векторы ненулевые. Предположим, что они линейно зависимы, т.е. существует такая ненулевая пара a, b действительных чисел, что a × а + b × в = 0. Если a ¹ 0, то умножим обе части последнего равенства скалярно на вектор а. Получим a × а² + b × (а, в) = 0. Так как (а, в) = 0 и а² ¹ 0, то a = 0. Противоречие. Следовательно, а и в линейно независимы.

9⁰. Если а₁, а₂, …, а_к и в₁, в₂, …, в_s – две системы линейно независимых векторов и каждый вектор первой системы ортогонален любому вектору второй, то система векторов а₁, а₂, …, а_к, в₁, в₂, …, в_s линейно независима.

Теорема 42. Для любого к (1 £ к £ n) Е_n = Е Å Е_к.

Доказательство. Пусть (е₁, е₂,..., е_к) – базис в Е_к и (е_{к +1}, е _{к + 2},..., е_n) – базис в Е . Из свойства 9⁰ следует, что (е₁, е₂,..., е_к, е_{к +1}, е _{к + 2},..., е_n) будет линейно независимой. Так как в ней n векторов, то это базис в Е_n. Следовательно, Е_n = Е + Е_к. Из свойства 7⁰ следует Е_n = Е Å Е_к.

Пусть Е_n = Е Å Е_к. Если а – любой вектор из Е_n, то а = а₁ + а₂, где а₁ Î Е_к, а₂ Î Е . Вектор а₁ называется проекцией вектора а на подпространство Е_к. Вектор а₂ называется ортогональной составляющей вектора а.

7.4. Ортонормированные базисы в евклидовом пространстве

Определение 51. Базис е = (е₁, е₂,..., е_n) пространства Е_n называется ортонормированным, если все его векторы единичные и попарно ортогональные.

Замечание. В примере 1 пункта 7.2 заданный базис является ортонормированным. Во втором примере этого пункта базис не ортонормированный.

Если базисные векторы единичные, но не все попарно ортогональны, то базис называется нормированным. Если базисные векторы попарно ортогональны, но не все единичные, то базис называется ортогональным.

Теорема 43. Любой базис евклидова пространства можно ортонормировать.

Доказательство. Пусть е = (е₁, е₂,..., е_n) – произвольный базис пространства Е_n. Доказательство проведём в два этапа. Сначала на основе данного базиса получим ортогональный базис, а затем полученный базис нормируем.

Пусть е₁¹ = е₁. Если е₂ ^ е₁, то возьмём е₂¹ = е₂. Если е₂ не ортогонален е₁. тонайдём коэффициент a так, чтобы вектор е₂¹ = a е₁ + е₂ был ортогонален вектору е₁¹. Так как вектор е₂¹ ¹ 0, то для этого необходимо и достаточно, чтобы (е₁¹, е₂¹) = 0, т.е. (е₁, a е₁ + е₂) = 0. Отсюда a е₁² + (е₁, е₂) = 0. Так как е₁ ¹ 0. то 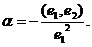Так как е₁¹ и е₂¹ ортогональны, то они линейно независимы. Вектор е₃¹ будем искать в виде е₃¹ = a₁ е₁¹ + a₂ е₂¹ + е₃. Для того, чтобы е₃¹ был ортогонален е₁¹ и е₂¹, необходимо и достаточно, чтобы (е₁¹, е₃¹) = (е₂¹, е₃¹) = 0. Получаем систему

Так как определитель этой системы отличен от нуля (по формуле 43) то система имеет и только одно решение. Следовательно,

вектор е₃¹ найдётся и только один. Так как векторы е₁¹, е₂¹, е₃¹ попарно ортогональны, то они линейно независимы. Если векторы е₁¹, е₂¹, …, е_n–1¹ уже получены, то вектор е_n¹ будем искать в виде е_n¹ = b₁ × е₁¹ + b₂ × е₂¹ + … + b_n–1 × е_n–1¹ + е_n. Так как вектор е_n¹ должен быть ортогонален ко всем предыдущим, то для нахождения коэффициентов b₁, b₂, …, b_n– ₁ получим систему уравнений (е₁¹, е_n¹) = (е₂¹, е_n¹) = … = (е_n–1¹, е_n¹) = 0. Можно показать, что эта система всегда имеет решение и только одно. Итак, базис е¹ = (е₁¹, е₂¹,..., е_n¹) –ортогональный. Разделив каждый полученный вектор на его длину, получим ортонормированный базис.

Теорема 44. Скалярное произведение в ортонормированном базисе имеет единичную матрицу Грама.

Доказательство следует из того, что в ортонормированном базисе (е_к, е_к) =1, (е_к, е_s)= 0, если к ¹ s.

Следствие. Если вектор а в ортонормированном базисе имеет координаты (х₁, х₂,…, х_n), то ½ а ½= (47).

Теорема 45. Определитель матрицы Грама и все её главные угловые миноры строго положительны.

Доказательство. Пусть в данном (но произвольном) базисе матрица Грама имеет вид

Г =

Пусть е = (е₁, е₂,..., е_n) ортонормированный базис и Т – матрица перехода от данного базиса к базису е. В базисе е матрица Грама – единичная. По формуле (43) Е = Т^Т ×Г ×Т. Отсюда 1 = | Г |×| Т |². Так как | Т |² > 0, то | Г | > 0.

Так как < е₁, е₂,..., е_к > – евклидово подпространство пространства Е_n с тем же скалярным произведением, то главный угловой минор матрицы Г будет для него матрицей Грама. Но тогда, по доказанному, этот минор положителен.

Примеры. Могут ли быть матрицами Грама следующие матрицы.

1. А =	Матрица А не может быть матрицей Грама, так как в матрице Грама все диагональные элементы должны быть положительными.
2. В =	Матрица В не может быть матрицей Грама, так как матрица Грама должна быть симметрична относительно главной диагонали.
3. С =	Матрица С не может быть матрицей Грама, так как \| С \| = –81 < 0, а определитель матрицы Грама должен быть положителен.
4. D =	Матрица D – симметрическая, диагональные элементы положительны, \| D \| = 5 > 0, = 7 > 0. Следовательно, D является матрицей Грама.

Теорема 46. Если в ортонормированном базисе а = (х₁, х₂, …, х_n) и в = (у₁, у₂, …, у_n), то (а, в) = х₁у₁ + х₂у₂ + … + х_nу_n (48).

Доказательство. В ортонормированном базисе скалярное произведение имеет единичную матрицу, поэтому

(а, в) = х^Т ×Е ×у = х^Т ×у = (х₁, х₂, …, х_n) × = х₁у₁ + х₂у₂ + … + х_nу_n.

Пример. В пространстве Е₄ задан ортонормированный базис и векторы а₁ = (2, 1, 1, 2) и а₂ = (–3, 2, –5, 1). Найти ортогональное дополнение к линейной оболочке L = < а₁, а₂ >.

Решение. Если L ^{^}, то в Î L ^{^} Û (а₁, в) = (а₂, в) = 0. Пусть в = (х₁, х₂, х₃, х₄).Так как базис ортонормированный, то (а₁, в) = 2 х₁ + х₂ + х₃ +2 х₄, (а₂, в) = –3 х₁ +2 х₂ –5 х₃ + х₄. Следовательно, в Î L ^{^} Û 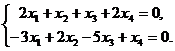Решая эту систему, получим, что

в = (– С₁ – 3С₂, С₁ – 8 С₂, С₁, 7 С₂), где С₁, С₂ – любые действительные числа.

Отсюда следует, что L ^{^} - двумерное линейное пространство, натянутое на векторы

в₁ = (–1, 1, 1, 0), в₂ = (–3, –8, 0, 7), т.е. L ^{^} = < в₁, в₂ >.

7.5. Изоморфизм евклидовых пространств

Определение 52. Два евклидовых пространства Е и Е¹ называются изоморфными, если они изоморфны как линейные пространства и для любых двух пар соответствующих векторов а, а¹ и в, в¹ выполняется равенство (а, в) = (а¹, в¹).

Теорема 47. Два конечномерных евклидова пространства Е и Е¹ изоморфны тогда и только тогда, когда dim E = dim E ¹.

Доказательство. Þ Пусть Е и Е¹ изоморфны. Тогда они изоморфны и как линейные пространства. Из свойств изоморфизма линейных пространств следует, что dim E = dim E ¹.

Ü Пусть dim E = dim E ¹ = n. Выберем в пространствах Е и Е¹ ортонормированные базисы е = (е₁, е₂,..., е_n) и е¹ = (е₁¹, е₂¹,..., е_n¹) соответственно. Зададим отображение j: Е ® Е¹ по следующему правилу. Если а Î Е и а = х₁ е₁ + х₂ е₂ + … + х_n е_n, то пусть j (а) = х₁ е₁¹ + х₂ е₂¹ + … + х_n е_n¹. Это отображение является, очевидно, изоморфизмом между линейными пространствами Е и Е¹. Покажем, что при этом отображении сохраняется скалярное произведение векторов. Пусть в Î Е и в = у₁ е₁ + у₂ е₂ + … + у_n е_n _.Тогда j (в) = у₁ е₁¹ + у₂ е₂¹ + … + у_n е_n¹ _.Так как базис е ортонормированный, то (а,в)= х₁у₁ + х₂у₂ +… + х_nу_n. Так как базис е¹ ортонормированный, то (j (а), j (в)) = х₁у₁ + х₂у₂ + … + х_nу_n. Следовательно, (а,в) = (j (а), j (в)). Итак, j - изоморфизм между Е и Е¹.

Следствие. Если на конечномерном линейном пространстве различными способами задавать скалярные произведения, то все получающиеся при этом евклидовы пространства будут изоморфными.

VIII. НЕКОТОРЫЕ ВИДЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ЕВКЛИДОВЫХ ПРОСТРАНСТВ

Так как евклидовы пространства являются линейными пространствами, то все свойства линейных преобразований линейных пространств верны и в евклидовых пространствах. Но все эти свойства связаны лишь с двумя алгебраическими операциями: сложением векторов и умножением вектора на элемент поля Р. В евклидовом пространстве есть ещё одна операция: скалярное умножение векторов. В зависимости от того как меняется скалярное произведение выделяются некоторые частные виды линейных преобразований.

8.1. Ортогональные линейные преобразования

Определение 53. Линейное преобразование j евклидова пространства Е называется ортогональным, если для любых векторов а и в из Е выполняется условие

(а, в) = ( j (а), j (в)) (49)

Свойства ортогональных преобразований.

Пусть j – ортогональное преобразование пространства Е.

1⁰. | а | = | j (а)| для любого вектора а.

| а | = = = | j (а)|.

2⁰. = для любых векторов а и .

3⁰. Пусть Е_n конечномерное евклидово пространство, е = (е₁, е₂,..., е_n) – базис в нём, А – матрица преобразования j и Г – матрица Грама в этом базисе. Тогда j (а) = А ×х, j () = А ×у, где х и у – столбцы координат векторов а и соответственно; (а, ) = х^Т ×Г ×у, (j (а), j ()) = (А ×х)^Т× Г ×(А ×у) = х ^Т×(А ^Т× Г × А)× у. Так как (а, ) = (j (а), j ()), то Г = А ^Т× Г × А. Итак, матрица ортогонального преобразования удовлетворяет условию

Г = А ^Т× Г × А (50)

Справедливо и обратное. Если в Е_n зафиксирован базис и Г – матрица Грама в этом базисе, то матрица А, удовлетворяющая условию (50), задаёт ортогональное преобразование.

Если базис е = (е₁, е₂,..., е_n) ортонормированный, то Г = Е и формула (50) примет вид

А^Т × А = Е, или А^Т = А^–1.

Определение 54. Квадратная матрица А называется ортогональной, если

А^Т = А^–1 (51).

Теорема 48. Линейное преобразование евклидова пространства является ортогональным тогда и только тогда, когда в ортонормированном базисе оно задаётся ортогональной матрицей.

Доказательство следует из свойства 3⁰ и определения 53.

Теорема 49. Квадратная матрица является ортогональной тогда и только тогда, когда сумма квадратов всех элементов любого столбца (или строки) равна 1, а сумма попарных произведений соответствующих элементов двух различных столбцов (или строк) равна нулю.

Доказательство следует из формулы 51.

Теорема 50. Линейное преобразование евклидова пространства является ортогональным тогда и только тогда, когда оно ортонормированный базис переводит в ортонормированный базис.

Доказательство. Þ Пусть j: Е_n ® Е_n ортогональное преобразование и пусть е = (е₁, е₂,..., е_n) ортонормированный базис в Е_n. Если А – матрица этого преобразования в базисе е, то А – ортогональная. Но тогда j (е) = е × А. Распишем это равенство, если

А = .

Получим j (е_к) = а_1ке₁ + а_2ке₂ + … + а _nке_n. Так как базис е ортонормированный, то (j (е_к))² = = (е_к)² = 1, т.е. все векторы j (е_к) единичной длины. По той же причине (j (е_к), j (е_р)) = а_1к ×а_1р + а_2к ×а_2р + … + а _nк ×а _nр = (е_к, е_р) = 0,

если к ¹ р, т.е. j (е_к) ^ j (е_р). Так как векторы системы j (е) попарно ортогональны, то они линейно независимы, т.е. j (е) – базис. Итак, j (е) – ортонормированный базис.

Ü Пусть е и j (е) – ортонормированные базисы. Тогда 1 = (j (е_к))² = и 0 = (j (е_к), j (е_р)) = а_1к ×а_1р + а_2к ×а_2р + … + а_nк ×а_nр при к ¹ р. Следовательно, по теореме 49, матрица А – ортогональная.

Теорема 51. Если матрица А ортогональная, то | А | = ± 1.

Действительно, если матрица А ортогональная, то А ^Т× А = Е. Отсюда | А ^Т× А | = | Е |, | А ^Т|×| А | = 1, | А |×| А | = 1, | А |² = 1, | А | = ±1.

Теорема 52. Собственные значения ортогонального преобразования могут быть только 1 или (–1).

Доказательство. Пусть l – собственное значение ортогонального преобразования j.

Тогда существует такой ненулевой вектор (х₁, х₂, …, х _n)^Т, что А ×х = l ×х, где А – матрица преобразования j. Равенство транспонируем и перейдём к сопряжённым числам, получим . Перемножим почленно оба равенства. . Так как А – действительная ортогональная матрица, то . Следовательно, . Отсюда 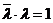, т.е. | l |² = 1. Но это и значит, что собственными значениями могут быть только числа 1 и (–1).

Теорема53. Собственные векторы ортогонального преобразования, принадлежащие различным собственным значениям ортогональны.

Доказательство. Для любых а и в из Е _n имеет место (а, в) = (j (а), j (в)) = (l₁ а, l₂ в) = = l₁ l₂ (а, в). Так как l₁ ¹ l₂, то, согласно предыдущей теоремы, l₁ =1, l₂ = –1. Следовательно, (а, в) = – (а, в). Отсюда (а, в) = 0. Так как а и в не нулевые, то они ортогональные.

8.2. Сопряженные линейные преобразования

Пусть j - линейное преобразование евклидова пространства Е_n.

Определение 55. Линейное преобразование j *: Е_n ® Е_n называется сопряжённым к преобразованию j, если для любых двух векторов а и в из Е_n выполняется условие

(а, j (в)) = (j * (а), в) (52)

Теорема 54. Матрицы сопряжённых преобразованийсвязаны формулой А = Г ^– ¹×(А *)^Т× Г.

Пусть в Е _n зафиксирован базис е = (е₁, е₂,..., е_n), Г – матрица Грама, А – матрица преобразования j и А * – матрица j *. Если х, у, у¹ и х * – столбцы координат векторов а, в, j (в)и j * (а)) соответственно, то (а, j (в)) = х ^Т× Г × у¹, (j * (а), в) = (х *)^Т ×Г × у. Используя равенство (52), получим х ^Т× Г × у¹ = х * ×Г × у. Используя связь координат вектора и его образа (формула (36)), получим у¹ = А ×у, х * = А * × х. Подставим в предыдущее равенство:

х ^Т× Г ×(А × у) = (А * ×х)^Т× Г ×у, х ^Т×(Г × А)× у = х ^Т×((А *)^Т× Г)× у. Отсюда Г × А = (А *)^Т× Г, или

А = Г ^– ¹×(А *)^Т× Г (53)

Следствие 1. А * = Г ^– ¹× А ^Т× Г (54).

Доказательство. Из формулы (53) следует, что (А *)^Т = Г ×А ×Г ^–1, А * = (Г ^–1)^Т× А ^Т× Г ^Т. Так как Г – симметрическая матрица, то Г ^Т = Г. Следовательно, А * = Г ^– ¹× А ^Т× Г.

Следствие 2. Сопряжённость линейных преобразований взаимна.

Доказательство следует из формул 53 и 54.

Следствие 3. Если базис ортонормированный, то А * = А ^Т.

Доказательство следует из того, что в ортонормированном базисе Г = Е.

Пример. В базисе е = (е₁, е₂, е₃, е₄) пространства Е₄ скалярное произведение заданоматрицей Грама Г = . Пусть А = – матрица линейного преобразования j в этом базисе. Найти матрицу сопряжённого преобразования.

Решение. Легко проверить, что Г удовлетворяет всем требованиям матрицы Грама. Используем формулу (54). Из неё А * = Г ^– ¹× А ^Т× Г. Нужно найти матрицу Г ^–1. Проверьте, что Г ^–1 = . Итак,

А * = × × = .

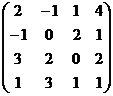Теорема 55. Если некоторое подпространство L евклидова пространства Е _n инвариантно относительно линейного преобразования j, то ортогональное дополнение L ^{^} инвариантно относительно сопряжённого преобразования j *.

Доказательство. Пусть а Î L, в Î L ^{^}. Тогда из условия j (а) Î L следует, что (в, j (а)) = 0. Но (в, j (а)) = (j * (в), а). Следовательно, (j * (в), а) для любого вектора а Î L. Следовательно, j * (в) Î L ^{^} для любого вектора в Î L ^{^}. Но это и означает, что подпространство L ^{^} инвариантно относительно j.

8.3. Самосопряженные (симметрические) линейные преобразования

Определение 56. Линейное преобразование называется самосопряжённым, если оно совпадает со своим сопряжённым преобразованием (j - самосопряжённое Û j = j *).

Из формулы (52) следует, что линейное преобразование j евклидова пространства будет самосопряжённым тогда и только тогда, когда (а, j (в)) = (j (а), в) (55).

Пусть в Е _n зафиксирован базис е = (е₁, е₂,..., е_n), Г – матрица Грама и А – матрица самосопряжённого преобразования j. В этом случае А * = А и формула (53) будет иметь вид: А = Г ^– ¹× А ^Т× Г. Если базис ортонормированный, то А = А ^Т, т.е. матрица А – симметрическая. Итак, верна

Теорема 56. Линейное преобразование является самосопряжённым тогда и только тогда, когда в ортонормированном базисе оно задаётся симметрической матрицей.

Теорема 56 объясняет тот факт, что самосопряжённое преобразование называют также симметрическим.

Отметим некоторые свойства симметрических преобразований.

1⁰. Тождественное преобразование является симметрическим.

Действительно, тождественное преобразование в любом базисе задается единичной матрицей. Но единичная матрица – симметрическая.

2⁰. Сумма симметрических преобразований есть преобразование симметрическое.

Это утверждение следует из того, что сумма двух симметрических матриц есть матрица симметрическая.

3⁰. Произведение симметрического преобразования на действительное число есть симметрическое преобразование.

Действительно, если симметрическую матрицу умножить на действительное число, то получится симметрическая матрица.

4⁰. Если симметрическое преобразование j имеет обратное преобразование j^– ¹, то j^– ¹ – симметрическое преобразование.

Это свойство тоже следует из свойств симметрических матриц.

5⁰. Если линейные преобразования j и y евклидова пространства симметрические, то их произведение будет симметрическим преобразованием тогда и только тогда, когда они перестановочны, т.е. j × y = y × j.

Действительно, для симметрических преобразований j и y имеем (j × y)* = y * × j * = y j.

j × y будет симметрическим тогда и только тогда (по определению), когда (j × y)* = j × y. отсюда следует, что j × y будет симметрическим тогда и только тогда, когда j × y = y j.

6⁰. Пусть j симметрическое преобразование евклидова пространства Е. Если Н – инвариантное подпространство преобразования j, то и ортогональное дополнение Н ^{^} является инвариантным подпространством преобразования j.

Это свойство следует из соответствующего свойства преобразования j *.

Теорема 57. Все корни характеристического многочлена симметрического преобразования действительные.

Доказательство. Пусть в пространстве Е_n зафиксирован ортонормированный базис е, пусть j симметрическое преобразование и А – его матрица в базисе е. Матрица А – симметрическая. Пусть l₀ – произвольный корень характеристического многочлена | А – lЕ |. Однородная система уравнений (А – l₀Е)× х = 0 имеет ненулевые решения, ибо определитель её равен нулю. Эти решения могут быть и комплексные. Пусть х = (х₁, х₂, …, х_n)^Т – одно из таких решений. Тогда Ах = l₀х. Умножим обе части этого матичного уравнения на строку ^Т, получим ^Т× А ×х = l₀ × ^Т ×х (*). Вычисляя ^Т ×х, получим ^Т ×х = 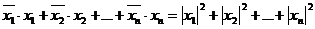. Отсюда следует, что ^Т ×х действительное число, не равное нулю. Покажем, что, если матрица А симметрическая, то число ^Т× А ×х тоже действительное. Число ^Т× А ×х можно рассматривать как квадратную матрицу первого порядка. Такая матрица не меняется при транспонировании, т.е. ^Т× А ×х = ( ^Т× А ×х)^Т = х ^Т× А ^Т× = х ^Т× А × . Кроме того . В двух последних равенствах правые части одинаковы, следовательно, равны и левые части, т.е. ^Т× А ×х = . Следовательно, число ^Т× А ×х действительное. Из равенства (*) следует, что l₀ – действительное число.

Следствие 1. Все характеристические корни симметрической матрицы А являются действительными.

Следствие 2. Симметрическое преобразование евклидова пространства имеет собственные векторы.

Теорема 58. Собственные векторы симметрического преобразования, принадлежащие различным собственным значениям, ортогональны.

Доказательство. Пусть j – симметрическое преобразование евклидова пространства Е_n, l₁, l₂, = его собственные значения и l₁ ¹ l₂. Пусть а и в – собственные векторы, принадлежащие собственным значениям l₁ и l₂ соответственно. Тогда j (а) = l₁ а, j (в) = l₂ в. По определению симметрического преобразования (а, j (в)) = (j (а), в). Отсюда (а, l₂ в) = (l₁ а, в), l₂ (а, в) = l₁ (а, в), (l₁ – l₂)×(а, в) = 0. Так как l₁ ¹ l₂, то (а, в) = 0. Так как собственные векторы не нулевые, то а ^ в.

Теорема 59. Линейное преобразование j: Е_n ® Е_n является симметрическим тогда и только тогда, когда в Е_n существует ортонормированный базис, состоящий из собственных векторов преобразования j.

Доказательство. Ü Пусть е = (е₁, е₂,..., е_n) – ортонормированный базис, состоящий из собственных векторов преобразования j. В этом случае j (е_к) = l_к e_k для любого к = 1, 2, …, n. Следовательно, в данном базисе преобразование j имеет диагональную, а поэтому и симметрическую матрицу, т.е. j – симметрическое преобразование.

Þ Пусть линейное преобразование j: Е_n ® Е_n симметрическое. Доказательство проведём методом математической индукции. При n = 1 каждый вектор отображается на пропорциональный ему вектор, т.е каждый вектор является собственным. Поэтому есть базис из собственных векторов.

Предположим, что утверждение теоремы верно для евклидова пространства размерности (n – 1). Пусть Е_n – евклидово пространство размерности n. По следствию 2 теоремы 54 j имеет собственные векторы. Пусть е₁ – собственный вектор, принадлежащий собственному значению l₁. Можно считать, что этот вектор единичный, иначе его можно нормировать. Пусть Е₁ = < е₁ >. Очевидно, j (Е₁) = Е₁. Ортогональное дополнение Е₁ ^Т тоже будет инвариантным относительно j. Так как dim Е₁ ^Т = n – 1, то в Е₁ ^Т существует ортонормированный базис, состоящий из собственных векторов преобразования j. Пусть это (е₂,..., е_n). Но тогда (е₁, е₂,..., е_n) – ортонормированный базис из собственных векторов в пространстве Е_n.

Из доказанной теоремы вытекает следующее утверждение.

Теорема 60. Любая симметрическая матрица А приводится к диагональному виду с помощью ортогональной матрицы.

Доказательство. Пусть А – симметрическая матрица. Её можно рассматривать как матрицу некоторого симметрического преобразования j в ортонормированном базисе е = (е₁, е₂,..., е_n) пространства Е_n. По теореме 56 в Е_n существует ортонормированный базис е¹ = (е₁¹, е₂¹,..., е_n¹), состоящий из собственных векторов преобразования j. Если А¹ – матрица j в базисе е¹, то А¹ – диагональная. Пусть Т – матрица перехода от базиса е к базису е¹. Тогда Т – ортогональная и А¹ = Т ^– ¹× А × Т.

Пример. Привести к диагональному виду матрицу

А =

Решение. Характеристический многочлен матрицы А

= (l – 1)³×(l + 3)

имеет корни l₁ = l₂ = l₃ = 1, l₄ = – 3. Все они являются собственными значениями матрицы А. Найдём соответствующие собственные векторы.

При l = 1 получаем систему уравнений

Ранг этой системы равен 1, поэтому фундаментальная системы состоит из 3-х решений, например, а₁ = (1, 1, 0, 0), а₂ = (1, 0, 1, 0), а₃ = (–1, 0, 0, 1). Полученную систему векторов нужно ортонормировать. Для этого нужно задать матрицу Грама. Так как скалярное произведение любое, то зададим Г = Е. Тогда получим

следующую ортонормированную систему:

е₁¹ = е₂¹ = , е₃¹ = .

При l = –3 получаем систему уравнений

Ранг этой системы равен 3, поэтому фундаментальная системы состоит из 1-го решения, например, а₄ = (1, –1, –1, 1). Нормируя его, получим е₄¹ =

(1, –1, –1, 1). Система векторов е₁¹, е₂¹, е₃¹, е₄¹ – ортонормированный базис из

собственных векторов. Матрица перехода от исходного базиса к базису е¹ будет

Т = .

Т ^– ¹ = .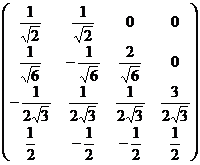

А = ТА¹Т ^– ¹ = × × .

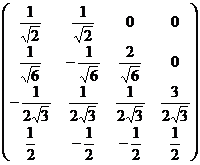Теорема 62. Для любого линейного преобразования j: Е_n ® Е_n преобразования j * j и jj * являются неотрицательными, т.е. эти преобразования симметрические, а все их собственные значения – неотрицательные числа.

Доказательство. (j * j)* = j * (j *) * = j * j. Следовательно, j * j – симметрическое преобразование. Пусть l – собственное значение преобразования j * j и а – соответствующий собственный вектор. Тогда ((j * j)(а), а) = (j * (j (а), а) = (j (а), j (а)) = =½ j (а)½². С другой стороны, ((j * j)(а), а) = (l а, а) = l ½ а ½². Следовательно, ½ j (а)½² = l ½ а ½². Так как а ¹ 0, то l ³ 0. Для преобразования jj * рассуждения аналогичны.

Определение 57. Симметрическое линейное преобразование называется положительно определённым, если для любого ненулевого вектора а выполняется неравенство (а, j (а)) > 0.

Теорема 61. Симметрическое преобразование является положительно определённым тогда и только тогда, когда все его собственные значения положительные.

Доказательство. Þ Пусть симметрическое преобразование j является положительно определённым. Тогда (а, j (а)) > 0 для любого вектора, в частности для любого собственного вектора. Но если а – собственный вектор, то j (а) = l а. Следовательно, 0 < (а, l а) = l (а, а). Так как для ненулевого вектора (а, а) > 0, то l > 0.

Ü Пусть все собственные значения симметрического преобразования j положительные. Выберем в пространстве Е_n базис е = (е₁, е₂,..., е_n), состоящий из собственных векторов этого преобразования. Если а = х₁ е₁ + х₂ е₂ + … + х_n е_n, то (а, j (а)) = ( = . Если а ¹ 0, то (а, j (а)) > 0, т.е. преобразование j положительно определённое.

Замечание. Симметрическое линейное преобразование называется неотрицательным, если для любого ненулевого вектора а выполняется неравенство (а, j (а)) ³ 0.

Симметрическое линейное преобразование называется отрицательно определённым, если для любого ненулевого вектора а выполняется неравенство (а, j (а)) < 0, для любого вектора а получим (а, j * j (а)) = (j (а), j (а)) ³ 0. Следовательно, преобразование j * j неотрицательное.

IX. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ

9.1. Линейные формы

Пусть L_n – n-мерное линейное пространство над полем Р и f –линейное отображение пространства L_n в поле Р (f: L_n ® Р).

Определение 58. Линейное отображение f: L_n ® Р называется линейной функцией или линейной формой, заданной на L_n.

Если е = (е₁, е₂,..., е_n) – базис в L_n, а – любой вектор из L_n, то а = х₁ е₁ + х₂ е₂ + … + х_n е_n, где х₁, х₂, …, х_n – любые элементы поля Р. Если f (е_к) = a_к, то f (а) = a₁х₁ + a₂х₂+ … + a_n х_n.

Следовательно, любую линейную форму можно задать в виде a₁х₁ + a₂х₂+ … + a_n х_n.

Легко показать, что множество всех линейных форм f: L_n ® Р является линейным пространством над полем Р.

9.2. Билинейные формы

Пусть L_n – n-мерное линейное пространство над полем Р.

Определение 59. Отображение f: (L_n ´ L_n) ® Р называется билинейной формой (или билинейной функцией), заданной на L_n

<== предыдущая лекция | следующая лекция ==>

Периодические издания и интернет ресурсы по философии | Семинар v- VI. Логическое направление в языкознании. Психологическое направление в языкознании.
Поделиться с друзьями:

Дата добавления: 2018-10-15; Мы поможем в написании ваших работ!; просмотров: 258 | Нарушение авторских прав

Поиск на сайте:

Лучшие изречения:

Лаской почти всегда добьешься больше, чем грубой силой. © Неизвестно
==> читать все изречения...
2418 - | 2279 -

© 2015-2025 lektsii.org - Контакты - Последнее добавление