Лекция 2
Формулы полной вероятности. Формулы Бейеса
Определение 8. Совокупность событий 
положительной вероятности на 
называется полной группой гипотез, если:
1) события попарно несовместны (см. определение 5);
2) 
.
Теорема 1 (формула полной вероятности). Если – полная группа гипотез на , то вероятность любого события 
можно вычислить по формуле:
 .
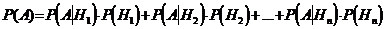| (5) |
Для доказательства этой теоремы нам понадобится следующая лемма, представляющая и самостоятельный интерес.
Лемма 1. Если события 
попарно несовместны (в смысле определения 5), то свойство s-аддитивности из определения 4 выполняется, то есть
Представим теперь себе ситуацию, что событие A осуществилось. Это обстоятельство позволяет пересмотреть вероятности исходных гипотез , то есть вычислить так называемые апостериорные вероятности гипотез (в отличие от априорных вероятностей, которые получаются до реализации какого-либо события). Речь идет об условных вероятностях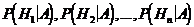 
.
Теорема 2 (формула Байеса). Для любого 
справедлива формула:
 .
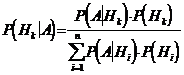| (6) |
Геометрическая вероятность
Рассмотрим теперь более подробно вероятностное пространство , на следующем примере.
Пример 2. Пусть 
– квадрат на плоскости 
, F – s-алгебра борелевских подмножеств этого квадрата (то есть наименьшая s-алгебра, содержащая все прямоугольники, входящие в квадрат), а 
для .
Лучше всего с этим пространством связывать эксперимент стрельбы в квадрат W (считается, что в этот квадрат стрелок попадает при любых условиях). Любое подмножество мы в этом случае интерпретируем как событие, состоящее в том, что стрелок попал в A. Смысл рассматриваемой вероятности P (или, как часто говорят, геометрической вероятности) хорошо согласуется с интуицией: чем больше площадь подмножества A, тем больше вероятность наступления события A.
Используя данное вероятностное пространство, можно достаточно легко получать геометрические обоснования многих фактов, доказанных нами ранее аналитически. Например, свойство 1 вероятности геометрически очевидно: площадь дополнительного к A множества 
равна площади квадрата W минус площадь самого множества A. Свойство 2 вероятности также становится прозрачным: так как 
это заштрихованная площадь на первом рисунке (см. пункт "Действия над событиями.Алгебра событий"), а в выражение 
два раза входит площадь множества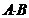 
, то ее нужно один раз отнять, и в результате получается формула 
. Точно так же легко интерпретируется свойство 3 вероятности, так как фраза "из события A следует событие B " геометрически означает, что множество A содержится во множестве B.
Проинтерпретируем теперь понятие независимости событий (см. определение 6). Пусть события A и B таковы, какими они показаны на следующем рисунке:
|
|
Здесь множество A представляет собой прямоугольник с шириной, равной 1, и высотой, равной a. Множество B представляет собой прямоугольник с шириной b и высотой, равной 1. Множество 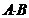– это пересечение прямоугольников A и B и также является прямоугольником. Заметим, что стороны всех прямоугольников параллельны соответствующим сторонам квадрата W. Из геометрических соображений следует, что 
. Поэтому выполняется условие независимости событий 
, то есть события A и B независимы. Оказывается, события такой конфигурации, как A и B, дают самые характерные примеры независимых событий. Подобная процедура построения независимых событий может быть существенно обобщена. Эти обобщения сплошь и рядом используются в теории вероятностей.
Схема Бернулли
Предположим, что мы производим некоторое испытание с двумя исходами (например, бросание монеты, когда исходами являются орел или решка, или вытягивание лотерейного билета, когда в результате испытания билет оказывается выигрышным либо проигрышным). Один исход данного испытания (имеющий вероятность p) будем считать успехом и обозначать единицей. Второй исход (имеющий вероятность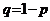 
) будем считать неудачей и обозначать нулем. Таким образом, совокупность исходов данного испытания мы отождествили с двуточечным множеством 
.
Повторим теперь это испытание независимым образом n раз. Результатом этого n -кратного эксперимента будут последовательности вида 
, где каждое число 
(
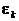) равно нулю либо единице. Например, если 
и мы получили последовательность 
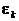, то это означает, что при первом и четвертом испытаниях нас постигла неудача, а второе и третье испытания были успешными. Ясно, что в качестве пространства элементарных событий следует взять множество W, состоящее из всевозможных цепочек вида , где каждое число () равно нулю либо единице. В качестве s-алгебры F выберем совокупность всех подмножеств множества W.
Остановимся более подробно на определении вероятности P. Обозначим через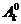 
(соответственно 
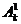) событие, состоящее в том, что при k -м испытании нас постигает неудача (соотв., при k -м испытании мы имеем успех). Очевидно, 
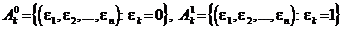. Так как при разных k испытания производятся независимым образом, то математически это должно означать, что любая система событий 
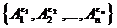должна быть независимой в совокупности в смысле определения 6. То есть вероятность события 
должна определяться формулой:
 .
| (7) |
Но легко видеть, что событие совпадает с элементарным событием , поэтому вероятность каждого элементарного события должна определяться той же формулой:
 .
| (8) |
Таким образом, мы построили конечное вероятностное пространство (бернуллиевское вероятностное пространство), моделирующее описанный выше n -кратный эксперимент.
Событие 
состоит в том, что в n испытаниях в схеме Бернулли наступило ровно m успехов.
Теорема 3. Справедлива формула:
 ,
| (9) |
где 
– число сочетаний из n элементов по m.
