Методы и средства исследований: конспект лекций / В.Л. Юша, Н.А. Райковский. – Омск: ОмГТУ, 2011.

ОЦЕНКА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ

Краткая теория, справочные таблицы и основные уравнения изложены в [1].

Задача 1: в результате наблюдений над случайными величинами х и у получена следующая совокупность данных при (n=10):

x: 2 4 1 7 3 11 14 15 21 4

y: 7 6 4 11 2 21 31 23 40 15

Необходимо проверить гипотезу о наличии корреляции между случайными величинами х и у с достоверностью α=0,95.

Решение

Находим:

Далее получаем оценки коэффициента корреляции:

Из таблицы 4.13 [1] для n=10 и r_0,95=0,632.

Так как r(r^*)=0,952(0,958)>r_0,95=0,632, наличие зависимости между величинами х и у следует признать значимой с достоверностью α=0,95.

Варианты заданий

Принять ряд выборочных значений случайной величины (n=10) по примеру заменив значения величин y_i согласно таблице 1.

Таблица 1 – Исходные данные

№ вар.	Значение случайной величины y_i
1	7	6	4	11	10	21	31	23	40	15
2	40	6	4	11	10	21	31	23	40	15
3	7	3	4	11	10	21	31	23	40	15
4	7	6	7	11	10	21	31	23	40	15
5	7	6	4	15	10	21	31	23	40	15
6	7	6	4	11	8	21	31	23	40	15
7	7	6	4	11	10	18	31	23	40	15
8	7	6	4	11	10	21	20	23	40	15
9	7	6	4	11	10	21	31	18	40	15
10	7	6	4	11	10	21	31	23	30	15
11	7	6	4	11	10	21	31	23	40	17
12	10	16	4	11	10	21	31	23	40	15
13	7	16	14	11	10	21	31	23	40	15
14	7	6	14	21	10	21	31	23	40	15
15	7	6	4	115	13	21	31	23	40	15
16	7	6	4	11	8	18	31	23	40	15
17	7	6	4	11	10	20	25	23	40	15
18	7	6	4	11	10	21	29	20	40	15
19	7	6	4	11	10	21	31	6	30	15
20	7	6	4	11	10	21	31	23	28	13
21	7	6	4	31	10	21	31	23	40	15
22	27	6	4	11	10	21	31	23	40	15
23	7	46	4	11	10	21	31	23	40	15
24	7	6	4	11	50	21	31	23	40	15
25	7	6	4	11	10	21	31	23	40	2

ОЦЕНКА КОРРЕЛЯЦИОННОГО ОТНОШЕНИЯ

Краткая теория, справочные таблицы и основные уравнения изложены в [1].

Задача 2: Проверить линейность корреляционной связи для выборки при доверительной вероятности α=0,95:

Yi	2	4	9	13	15
Xi	1,3,4	7,8,12	14,19,21	11,9,6	8,7,3

Решение

Имеем k=5, n_i=3 и n=15.

Вычисляем далее:

Тогда:

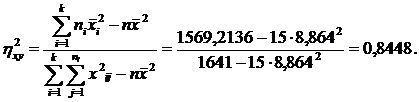
Вычисляем далее:

Из таблицы [1, Приложение П.2] находим F_0,95(f ₁, f ₂)= F_0,95(4;10)=3,5, где

f ₁ = k -1=5-1=4;

f ₂ = n - k =15-5=10.

Полученная величина l больше критического значения F_0,95(4,10)=3,5, следовательно, необходимо признать наличие существенной нелинейной связи между х и у.

Варианты заданий

Принять ряд выборочных значений случайной величины, по примеру заменив значения величин y_i согласно таблице 2.

Таблица 2 – Исходные данные

№ вар.	Значение случайной величины y_i
1	3	4	9	13	15
2	4	4	9	13	15
3	5	4	9	13	15
4	6	4	9	13	15
5	7	4	9	13	15
6	3	5	9	13	15
7	3	6	9	13	15
8	3	7	9	13	15
9	3	8	9	13	15
10	3	9	9	13	15
11	3	10	9	13	15
12	3	4	8	13	15
13	3	4	7	13	15
14	3	4	6	13	15
15	3	4	15	13	15
16	3	4	9	14	15
17	3	4	9	15	15
18	3	4	9	16	15
19	3	4	9	11	15
20	3	4	9	8	15
21	3	4	9	13	10
22	3	4	9	13	11
23	3	4	9	13	12
24	3	4	9	13	13
25	3	4	9	13	14

ЧАСТНАЯ И МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ

Краткая теория, справочные таблицы и основные уравнения изложены в [1].

Задача 3: Вычислить коэффициенты частной и множественной корреляции и проверить из значимость при доверительной вероятности α=0,95 для данных, приведенных ниже (n=10, k=3)

Таблица 3 – Исходные данные

x_i	1	3	4	7	12	4	19	21	1	3
y_i	12	42	58	71	68	50	49	85	18	26
z_i	41	12	7	3	14	27	38	13	64	75

Решение

Найдем парные коэффициенты корреляции.

Вычисляем коэффициент r_xy:

По аналогии вычисляем коэффициент r_xz:

По аналогии вычисляем коэффициент r_yz:

Вычислим теперь частные (парные) коэффициенты корреляции:

Вычислим множественные коэффициенты корреляции:

Вычислим t-статистики для проверки значимости частных (парных) коэффициентов корреляции:

- для проверки

-для проверки

- для проверки

Для α=0,95 и f = n - k =7 из [1, Приложени П.1] для t-распределения имеем . Видим, что

Следовательно, наличие частной корреляции отклоняется с достоверностью α=0,95.

Для коэффициентов множественной корреляции находим критическое значение [1, таблица 4.14] при k=3, n - k =7 и α=0,95. Имеем r_1,23(0,95)=0,758.

Так как ни один множественный коэффициент корреляции (r_x_,_yz=0,596 r_y_,_xz=0,689 и r_z_,_xy=0,516) не превышает критическое значение 0,758, то и наличие множественной корреляции отклоняется с достоверностью 0,95.

Варианты заданий

Принять значения случайной величины по примеру (таблица 3), заменив значения величин 1-го столбца согласно таблице 4.

Таблица 4 – Исходные данные

№ вар.	Значение случайной величины y_i
1	2	12	41
2	3	12	41
3	4	12	41
4	5	12	41
5	6	12	41
6	7	12	41
7	2	14	41
8	2	16	41
9	2	18	41
10	2	20	41
11	2	12	35
12	2	12	30
13	2	12	28
14	2	12	25
15	2	12	20
16	2	12	15
17	2	12	10
18	2	12	45
19	2	12	50
20	10	12	41
21	15	12	41
22	20	12	41
23	2	5	41
24	2	20	41
25	2	25	41

Методы и средства исследований: конспект лекций / В.Л. Юша, Н.А. Райковский. – Омск: ОмГТУ, 2011. – 96 с.