Дифференциальное уравнение вида
 (7.170)
(7.170)
где 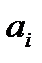
 действительные постоянные числа,
действительные постоянные числа,  непрерывная функция на рассматриваемом интервале
непрерывная функция на рассматриваемом интервале 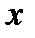 , неизвестная функция
, неизвестная функция  и ее производные
и ее производные  входят в уравнение линейно, называется линейным неоднородным дифференциальным уравнением
входят в уравнение линейно, называется линейным неоднородным дифференциальным уравнением  го порядка с постоянными действительными коэффициентами. В частности неоднородное уравнение второго порядка имеет вид
го порядка с постоянными действительными коэффициентами. В частности неоднородное уравнение второго порядка имеет вид
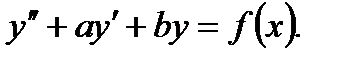 (7.171)
(7.171)
Из теории линейных дифференциальных уравнений известно, что общее решение линейного неоднородного уравнения (7.170) равно сумме общего решения соответствующего ему однородного уравнения (7.153) и одногочастного решения неоднородного уравнения (7.170), то есть
 (7.172)
(7.172)
Общее решение однородного уравнения 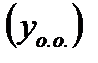 находим методом Эйлера. Для нахождения
находим методом Эйлера. Для нахождения
частного решениянеоднородного уравнения (7.170) можно пользоваться методом
неопределенных коэффициентов (метод подбора), если правая часть (7.170) имеет вид
 (7.173)
(7.173)
где  многочлен степени
многочлен степени  относительно
относительно 
 многочлен степени
многочлен степени 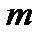 относительно
относительно 

Если число 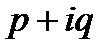 не совпадает ни с одним корнем
не совпадает ни с одним корнем  характеристического уравнения, то частное решение
характеристического уравнения, то частное решение  надо искать в виде
надо искать в виде
 (7.174)
(7.174)
где  и
и  многочлены степени
многочлены степени  с неопределенными коэффициентами.
с неопределенными коэффициентами.
Если число 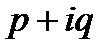 совпадает с
совпадает с  корнями характеристического уравнения, то частное решение неоднородного уравнения надо искать в виде
корнями характеристического уравнения, то частное решение неоднородного уравнения надо искать в виде
 (7.175)
(7.175)
где  и
и  многочлены степени
многочлены степени  с неопределенными коэффициентами. Отметим также, что если правая часть неоднородного уравнения (7.173) представляет собой сумму из
с неопределенными коэффициентами. Отметим также, что если правая часть неоднородного уравнения (7.173) представляет собой сумму из  функций вида (7.173), то частное решение такого неоднородного уравнения равно сумме частных решений неоднородного уравнения (7.170) с правыми частями, равными, соответственно,
функций вида (7.173), то частное решение такого неоднородного уравнения равно сумме частных решений неоднородного уравнения (7.170) с правыми частями, равными, соответственно,  то есть
то есть
 (7.176)
(7.176)
Пример 7.27. Найти общее решение линейного неоднородного уравнения
 (7.177)
(7.177)
Решение. Характеристическое уравнение  имеет корни
имеет корни  Общее решение однородного уравнения
Общее решение однородного уравнения 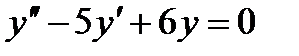 имеет вид
имеет вид
 (7.178)
(7.178)
где  и
и  произвольные постоянные. Так как согласно правой части (7.177)
произвольные постоянные. Так как согласно правой части (7.177)  и
и  не совпадает ни с одним корнем характеристического уравнения, то частное решение исходного неоднородного уравнения ищем в виде
не совпадает ни с одним корнем характеристического уравнения, то частное решение исходного неоднородного уравнения ищем в виде
 (7.179)
(7.179)
где  пока неопределенные постоянные коэффициенты. Подставляя
пока неопределенные постоянные коэффициенты. Подставляя 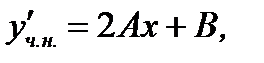
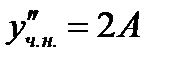 в исходное уравнение (7.177), получим
в исходное уравнение (7.177), получим
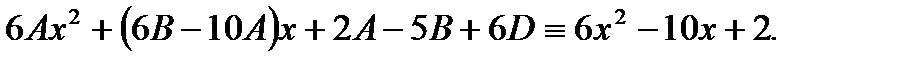 (7.180)
(7.180)
Приравнивая коэффициенты при одинаковых степенях  в левой и правой частях (7.180),
в левой и правой частях (7.180),
приходим к системе алгебраических уравнений относительно неопределенных коэффициентов
 (7.181)
(7.181)
Отсюда  Подставляя найденныезначения
Подставляя найденныезначения  в (7.179), получим
в (7.179), получим
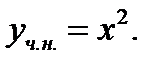 (7.182)
(7.182)
Общее решение уравнения (7.177) согласно (7.172) будет иметь вид
 (7.183)
(7.183)
где  и
и  произвольные постоянные.
произвольные постоянные.
Ответ: 
Пример 7.28. Найти частное решение уравнения (задача Коши)
 (7.184)
(7.184)
Решение. Характеристическое уравнение  соответствующего однородного уравнения
соответствующего однородного уравнения  имеет корни
имеет корни  Общее решение однородного уравнения запишется в виде
Общее решение однородного уравнения запишется в виде
 (7.185)
(7.185)
где  и
и  произвольные постоянные. Поскольку
произвольные постоянные. Поскольку  и число
и число  совпадает с одним корнем характеристического уравнения, то частное решение исходного неоднородного уравнения ищем в виде
совпадает с одним корнем характеристического уравнения, то частное решение исходного неоднородного уравнения ищем в виде
 (7.186)
(7.186)
где  пока неопределенный постоянный коэффициент. Подставляя (7.186) в исходное уравнение (7.184) и проводя вычисления, получим
пока неопределенный постоянный коэффициент. Подставляя (7.186) в исходное уравнение (7.184) и проводя вычисления, получим  Следовательно,
Следовательно, 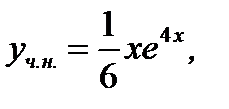 а общее решение исходного неоднородного уравнения запишется в виде
а общее решение исходного неоднородного уравнения запишется в виде
 (7.187)
(7.187)
Теперь перейдем к нахождению частного решения исходного уравнения. Учет начальных условий Коши (см. (7.184)) приводит к следующей системе уравнений для определения 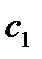 и
и 
 (7.188)
(7.188)
Отсюда имеем
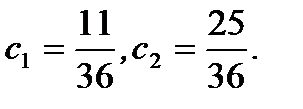 (7.189)
(7.189)
Из (7.187) с учетом (7.189) получим решение задачи Коши для исходного неоднородного уравнения в виде
 (7.190)
(7.190)
Ответ: 
Пример 7.29. Решить уравнение
 (7.191)
(7.191)
Решение. Характеристическое уравнение  соответствующего однородного уравнения
соответствующего однородного уравнения  имеет корни
имеет корни 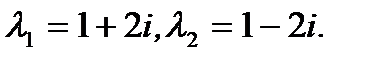 Поэтому общее решение однородного уравнения имеет вид
Поэтому общее решение однородного уравнения имеет вид
 (7.192)
(7.192)
где  и
и  произвольные постоянные.
произвольные постоянные.
Частные решения уравнения (7.191) найдем методом неопределенных коэффициентов. В правой части уравнения (7.191) стоит сумма двух функций  и
и  каждую из которых можно представить в виде (7.173). Для функции
каждую из которых можно представить в виде (7.173). Для функции  имеем
имеем 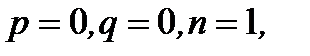 а для функции
а для функции  имеем
имеем  Согласно (7.176) частное решение уравнения (7.191) складывается из двух частных решений
Согласно (7.176) частное решение уравнения (7.191) складывается из двух частных решений
 (7.193)
(7.193)
где  частное решение неоднородного уравнения
частное решение неоднородного уравнения
 (7.194)
(7.194)
a  частное решение неоднородного уравнения
частное решение неоднородного уравнения
 (7.195)
(7.195)
 ищем в виде (
ищем в виде ( и это число не совпадает ни с одним корнем характеристического уравнения)
и это число не совпадает ни с одним корнем характеристического уравнения)

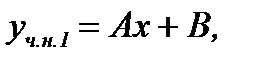 (7.196)
(7.196)
где  и
и  пока неопределенные постоянные коэффициенты. Подставляя
пока неопределенные постоянные коэффициенты. Подставляя  в (7.194) и производя вычисления, найдем
в (7.194) и производя вычисления, найдем  Следовательно,
Следовательно,

 (7.197)
(7.197)
 ищем в виде (
ищем в виде ( и это число не совпадает ни с одним корнем характеристического уравнения)
и это число не совпадает ни с одним корнем характеристического уравнения)
 (7.198)
(7.198)
где  и
и  пока неопределенные постоянные коэффициенты. Подставляя
пока неопределенные постоянные коэффициенты. Подставляя  в (7.195) и производя вычисления, найдем
в (7.195) и производя вычисления, найдем  Следовательно,
Следовательно,
 (7.199)
(7.199)
Тогда согласно (7.193) имеем
 (7.200)
(7.200)
Окончательно, общее решение исходного неоднородного уравнения запишется в виде
 (7.201)
(7.201)
Ответ: 
Задачи с ответами.
7.4.1. Найти общее решение обыкновенного дифференциального уравнения первого порядка

Ответ: 
7.4.2. Найти решение задачи Коши

Ответ: 
7.4.3. Найти общее решение обыкновенного дифференциального уравнения первого порядка

Ответ: 
7.4.4. Найти общее решение обыкновенного дифференциального уравнения первого порядка

Ответ: 
7.4.5. Найти общее решение обыкновенного дифференциального уравнения первого порядка
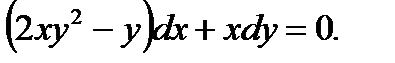

Ответ: 

7.4.6. Найти общее решение обыкновенного дифференциального уравнения второго порядка


Ответ: 

7.4.7. Найти общее решение линейного однородного дифференциального уравнения второго порядка


Ответ: 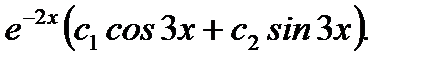
7.4.8. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка


Ответ: 

7.4.9. Найти общее решение линейного однородного дифференциального уравнения третьего порядка


Ответ: 

7.4.10. Национальный доход 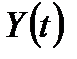 в простой макроэкономической модели Калецкого описывается дифференциальным уравнением первого порядка
в простой макроэкономической модели Калецкого описывается дифференциальным уравнением первого порядка

где  Найти
Найти 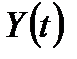 ,если
,если 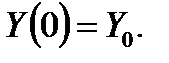

Ответ: 

7.4.11. Функция спроса  зависит от времени по формуле
зависит от времени по формуле  а функция предложения
а функция предложения  зависит от времени по формуле
зависит от времени по формуле  где
где  цена товара. Найти зависимость равновесной цены от времени, если в начальный момент времени
цена товара. Найти зависимость равновесной цены от времени, если в начальный момент времени 

Ответ: 

7.4.12. Число новорожденных за единицу времени (один год) пропорционально численности населения с коэффициентом  а число умерших – с коэффициентом
а число умерших – с коэффициентом  Найти формулу. Определяющую численность населения
Найти формулу. Определяющую численность населения  через
через 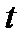 лет, если в настоящий момент она равна
лет, если в настоящий момент она равна 
Ответ: 

7.4.13. Цена товара в начале составляет 36 рублей, а через 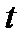 недель –
недель –  рублей. Если спрос
рублей. Если спрос 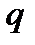 определяется равенством
определяется равенством  а предложение –
а предложение –  то как должна изменяться цена товара
то как должна изменяться цена товара  , чтобы спрос равнялся предложению.
, чтобы спрос равнялся предложению.
Ответ: 
7.4.14. Полные издержки  есть функция объема производства
есть функция объема производства  Найти функцию издержек
Найти функцию издержек  если известно, что предельные издержки для всех значений
если известно, что предельные издержки для всех значений  равняются средним издержкам
равняются средним издержкам 
Ответ: 
7.4.15. Функции спроса и предложения на товар зависят от времени 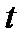 по формулам:
по формулам:
 Найти зависимость равновесной цены от времени.
Найти зависимость равновесной цены от времени.
Ответ: 






