Дифференциальным уравнением  го порядка
го порядка 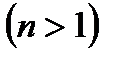 называется уравнение вида
называется уравнение вида
 (7.105)
(7.105)
или
 (7.106)
(7.106)
если оно разрешимо относительно старшей производной. После решения уравнения (7.105) либо (7.106) получим общее решение в виде
 (7.107)
(7.107)
или общий интеграл в виде
 (7.108)
(7.108)
где  произвольные постоянные.
произвольные постоянные.
Решить задачу Коши для дифференциального уравнения (7.105) (или (7.106)) означает найти частное решение данного уравнения, удовлетворяющего  заданным начальным условиям
заданным начальным условиям
 (7.109)
(7.109)
С помощью начальных условий (7.109) получается система алгебраических уравнений для определения произвольных постоянных 
Ниже приводятся некоторые случаи уравнений порядка выше первого, когда удается понизить порядок уравнения, что облегчает его интегрирование.
1. В уравнение входит только производная неизвестной функции наивысшего порядка, то есть оно имеет вид
 (7.110)
(7.110)
В этом случае решение уравнения находится  кратным интегрированием функции
кратным интегрированием функции 
Пример 7.18. Решить уравнение третьего порядка
 (7.111)
(7.111)
Решение. Перепишем уравнение (7.111) в виде
 (7.112)
(7.112)
Интегрируя последнее, получим
 (7.113)
(7.113)
Далее имеем
 (7.114)
(7.114)
И окончательно, интегрируя (7.114), получим общее решение уравнения (7.111) в виде
 (7.115)
(7.115)
где  произвольные постоянные.
произвольные постоянные.
Ответ: 
2. Уравнение не содержит искомой функции 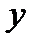 и ее производных до порядка
и ее производных до порядка  включительно, то есть имеет вид
включительно, то есть имеет вид
 (7.116)
(7.116)
Замена переменной по формуле 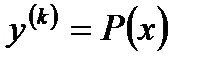 с учетом того, что
с учетом того, что 

 снижает порядок уравнения (7.116) до
снижает порядок уравнения (7.116) до  Действительно, после указанной замены получим
Действительно, после указанной замены получим
 (7.117)
(7.117)
общее решение которого будет иметь вид
 (7.118)
(7.118)
Искомая функция  далее определяется из уравнения
далее определяется из уравнения  путем
путем  кратного интегрирования функции
кратного интегрирования функции 
Пример 7.19. Решить уравнение третьего порядка
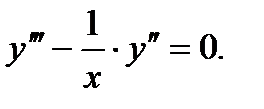 (7.119)
(7.119)
Решение. Данное уравнение не содержит  и
и  Полагая
Полагая 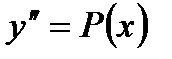 и учитывая, что
и учитывая, что  из (7.119) получим дифференциальное уравнение первого порядка с разделяющимися переменными относительно
из (7.119) получим дифференциальное уравнение первого порядка с разделяющимися переменными относительно 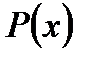
 (7.120)
(7.120)
решение которого имеет вид
 (7.121)
(7.121)
где  произвольная постоянная. Таким образом, уравнение
произвольная постоянная. Таким образом, уравнение  преобразуется к виду
преобразуется к виду
 (7.122)
(7.122)
Интегрируя последнее уравнение два раза, получим
 (7.123)
(7.123)
Поскольку  произвольные постоянные, то окончательно общее решение уравнения (7.119) можно записать в виде
произвольные постоянные, то окончательно общее решение уравнения (7.119) можно записать в виде
 (7.124)
(7.124)
где  произвольные постоянные.
произвольные постоянные.
Ответ: 
3.Уравнение не содержит в явном виде независимую переменную  то есть имеет вид
то есть имеет вид
 (7.125)
(7.125)
Порядок уравнения в этом случае можно понизить на единицу заменой переменной
 (7.126)
(7.126)
Так как
 (7.127)
(7.127)
и так далее, то производные 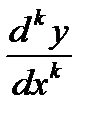 выражаются через производные порядка не выше
выражаются через производные порядка не выше 
от  по
по 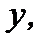 что и приводит к понижению порядка уравнения (7.125) на единицу.
что и приводит к понижению порядка уравнения (7.125) на единицу.
Пример 7.20. Решить уравнение второго порядка
 (7.128)
(7.128)
Решение. Полагая
 (7.129)
(7.129)
из (7.128) получим уравнение первого порядка относительно 
 (7.130)
(7.130)
Отсюда имеем
1.  (7.131)
(7.131)
где  произвольная постоянная.
произвольная постоянная.
2. 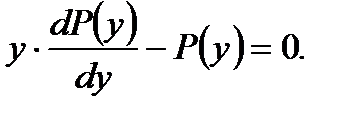
 (7.132)
(7.132)
Общее решение уравнения (7.132) с разделяющимися переменными имеет вид

 (7.133)
(7.133)
где  произвольная постоянная. Разделяя переменные в (7.133) и интегрируя, получим решение уравнения (7.128) в виде
произвольная постоянная. Разделяя переменные в (7.133) и интегрируя, получим решение уравнения (7.128) в виде
 (7.134)
(7.134)
Заметим, что решение (7.131) получается из (7.134) при 
Ответ: 
4.Левая часть уравнения
 (7.135)
(7.135)
является производной некоторой функции 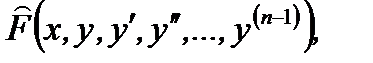 то есть
то есть
 (7.136)
(7.136)
В этом случае интегрирование очевидного уравнения
 (7.137)
(7.137)
дает возможность получить первый интеграл уравнения (7.135)
 (7.138)
(7.138)
где  произвольная постоянная. Заметим, что уравнение (7.138) уже является дифференциальным уравнением
произвольная постоянная. Заметим, что уравнение (7.138) уже является дифференциальным уравнением  порядка.
порядка.
Пример 7.21. Решить уравнение второго порядка
 (7.139)
(7.139)
Решение. Учитывая, что  из (7.139) получим уравнение
из (7.139) получим уравнение
 (7.140)
(7.140)
Интегрирование последнего приводит к первому интегралу
 (7.141)
(7.141)
где  произвольная постоянная. Разделяя переменные в (7.141) и интегрируя, получим общее решение исходного уравнения в виде
произвольная постоянная. Разделяя переменные в (7.141) и интегрируя, получим общее решение исходного уравнения в виде
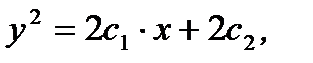 (7.142)
(7.142)
где  произвольная постоянная.
произвольная постоянная.
Ответ: 
Отметим, что в (7.142)  и
и  такие произвольные постоянные, которые удовлетворяют условию
такие произвольные постоянные, которые удовлетворяют условию 
5. Левая часть уравнения
 (7.143)
(7.143)
является однородной функцией 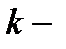 ой степени относительно неизвестной функции
ой степени относительно неизвестной функции  и ее производных, то есть
и ее производных, то есть
 (7.144)
(7.144)
где  некоторое натуральное число. Порядок уравнения в этом случае понижается на единицу следующей заменой переменной
некоторое натуральное число. Порядок уравнения в этом случае понижается на единицу следующей заменой переменной
 (7.145)
(7.145)
Учитывая, что
 (7.146)
(7.146)
и однородность функции  после подстановки (7.145) и (7.146) в исходное уравнение приходим к уравнению порядка
после подстановки (7.145) и (7.146) в исходное уравнение приходим к уравнению порядка 
Пример 7.22. Решить задачу Коши
 (7.147)
(7.147)
Решение. Левая часть уравнения (7.147) есть однородная функция второй степени относительно  Полагая
Полагая 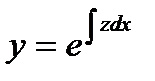 и подставляя в (7.147) с учетом (7.146), поучим следующее уравнение первого порядка относительно
и подставляя в (7.147) с учетом (7.146), поучим следующее уравнение первого порядка относительно 
 (7.148)
(7.148)
которое имеет очевидное решение
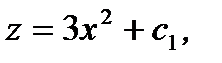 (7.149)
(7.149)
где  произвольная постоянная. Далее имеем
произвольная постоянная. Далее имеем
 (7.150)
(7.150)
где 
Частное решение задачи получается из общего решения (7.150) при конкретных значениях  и
и  , которые определяются с помощью начальных условий (см. (7.147))
, которые определяются с помощью начальных условий (см. (7.147))
 (7.151)
(7.151)
Решая (7.151), получим  Подстановка полученных значений
Подстановка полученных значений  и
и  в (7.150) приводит к решению задачи Коши в виде
в (7.150) приводит к решению задачи Коши в виде
 (7.152)
(7.152)
Ответ: 




