1. Пропорциональные цилиндрические образцы Размеры в мм. Общая длина L = l + 2 h + 2 h 1
| Общие размеры | Длинные образцы | Короткие образцы | ||||||||
| d 0 | D | h | h1 | R | № | l | l 0 | № | l 0 | l |
| 8 | 13 | 10 | 3 | 2 | 16 | 80 | 88 | 16к | 40 | 48 |
| 6 | 12 | 10 | 2,5 | 1,5 | 17 | 60 | 66 | 17к | 30 | 36 |
| 5 | 11 | 10 | 2,5 | 1,5 | 18 | 50 | 55 | 18к | 25 | 30 |
| 4 | 9 | 8 | 2,5 | 1,5 | 19 | 40 | 44 | 19к | 20 | 24 |
2. Плоские образцы без головок. Размеры в мм. Общая длина L = l +2 h
| Общие размеры | Длинные | Короткие | ||||||
| а 0 | b 0 | l 0 | № | l 0 | l | № | l 0 | l |
| 6 | 30 | 50 | 94 | 150 | 165 | 94к | 75 | 90 |
| 5 | 30 | 50 | 95 | 140 | 155 | 95к | 70 | 85 |
| 4 | 30 | 40 | 96 | 120 | 135 | 96к | 60 | 75 |
| 3 | 20 | 40 | 97 | 90 | 100 | 97к | 45 | 55 |
| 2 | 20 | 40 | 98 | 70 | 80 | 98к | 35 | 45 |
| 1 | 20 | 40 | 99 | 50 | 60 | 99к | 25 | 35 |
| 0,5 | 20 | 40 | 100 | 40 | 50 | 100к | 20 | 30 |
На диаграмме истинных напряжений присутствуют те же характерные точки, что и на диаграмме σусл(εусл)за исключением σв. Напряжения σпц, σупр, σтв, σтн, σ0,2, σв, σр были приняты как характеристики прочности металла.
1. 1 Предел пропорциональности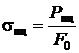 
определяет величину напряжений, ограничивающих область упругих деформаций: обычно принято считать, что при σ<σпц выполняется закон Гука σ= Е ε. Однако использование высокоточных испытательных машин показало, что в чистом виде закон Гука выполняется лишь до величин деформаций ε≈1·10−3 %, в связи с чем ввели понятие физического и технического пределов пропорциональности. Первый определяется в тот момент, когда пластическая деформация равна 1·10−3 % или εпц=0,00001; второй − когда тангенс угла наклона кривой σ(ε)или σусл(εусл)изменит свое значение в полтора раза. В данной лабораторной работе необходимо определить технический предел пропорциональности. О физическом пределе пропорциональности упоминать в дальнейшем не будем.
2. Предел упругости 
−характеристика прочности металла, близкая по значению и смыслу к пределу пропорциональности. Отличие состоит в том, что σупр определяется при остаточной деформации образца 0,05%, т.е. ε=0,0005.
3. Предел текучести. На рис. 2 видно, что некоторые металлы имеют на кривой Р (D l)или σ(ε)характерный участок, на котором пластическая деформация происходит при постоянной силе или напряжении. Этот участок называют площадкой текучести. Начало этого участка представляет собой некоторый барьер – «зуб текучести», преодолев который, металл деформируется при постоянных напряжениях σ=const. Наличие зуба текучести связывают с отрывом дислокаций от облаков примесных атомов или вакансий, вследствие чего их дальнейшее перемещение требует меньших напряжений.
На диаграммах с площадкой текучести определяют два предела текучести − верхний и нижний: 
, 
. Эти напряжения соответствуют началу активной пластической деформации. Интервал напряжений σтв − σпц называют упруго-пластической зоной деформации.
На кривых σ(ε)для металлов, у которых отсутствует в явном виде площадка текучести (рис.2, II), за момент начала активной пластической деформации принимают напряжения, соответствующие пластической деформации ε = 0,2%, т.е. ε = 0,002. Для подобных материалов зона упруго-пластических деформаций простирается между σ0,2 и σпц.
Характеристики металла σпц, σупр, σтв, σтн или σ0,2 мало отличаются друг от друга, если определять их по диаграммам условных или истинных напряжений. Это связано с тем, что при малых значениях деформаций D l или 
площадь поперечного сечения образца изменяется незначительно, т.е. F ≈ F 0. Ситуация существенно изменяется на участке деформационного упрочнения σтн<σ<σв,где деформация D l или ε достигает больших значений. В зоне активной пластической деформации и деформационного упрочнения истинные напряжения при растяжении могут значительно превышать условные σ>σусл, поскольку при растяжении F < F 0для тех же величин деформации ε.
Известно, что деформационное упрочнение обусловлено изменением структуры из-за существенного увеличения плотности дефектов кристаллического строения − вакансий, дислокаций, границ и др. Эти дефекты, располагаясь в объеме зерен определенным порядком, образуют по мере возрастания деформаций клубковую, ячеистую, фрагментированную структуры. Упрочнение металла происходит вплоть до разрушения образца.
4. Предел прочности, или временное сопротивление 
характеризует максимальные напряжения на кривой σусл(εусл). При напряжениях σ=σв вдеформируемом образце пластическая деформация локализуется в узкой области, образуется шейка, площадь сечения образца в этом месте уменьшается. Это снижение значения F требует для продолжения деформации меньшей силы Р, поэтому кривая Р( D 1), которая записывается на испытательной машине, опускается ниже Р в. В связи с этим кривая условных напряжений σусл(εусл)также опускается ниже σв. Дальнейшая пластическая деформация и деформационное упрочнение происходят только в шейке образца, в минимальном его сечении, в котором происходит окончательный разрыв образца. После образования шейки пластическая деформация в остальном объеме металла практически прекращается.
На диаграмме истинных напряжений σ(ε)подобного явления не наблюдается − происходит лишь изменение интенсивности упрочнения. Отметим, что при построении диаграммы истинных напряжений в качестве площади F принимается площадь деформируемого в шейке сечения металла.
5. Истинное сопротивление разрыву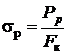 
,(F к − площадь поперечного сечения образца в месте разрыва) характеризует напряжения, которые приводят к макроскопическому разрушению образца. На диаграмме истинных напряжений σ(ε)напряжения σр занимают наиболее высокое место.
При испытаниях металлов на растяжение определяют и характеристики пластичности металла − максимальное удлинение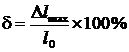 
, где D l max − максимальное удлинение образца, а также относительное сужение сечения образца в шейке после разрушения 
.
В материаловедении для определения свойств металлов часто пользуются диаграммами условных напряжений, по которым можно найти значения σпц, σупр, σтв, σтн, σ0,2, σв, Y и δ. В практике пластической обработки металлов значительно большее значение имеют диаграммы истинных напряжений σ(ε).Пользуясь результатами опытов на растяжение в виде диаграмм σ(ε),можно предсказать поведение металла в любом процессе пластической деформации − при прокатке, осадке, прессовании, волочении и т.д. Это позволяет так называемая гипотеза «единой кривой». Суть ее состоит в том, что для любой схемы напряженно деформированного состояния и 
зависимость интенсивности напряжений σ i от интенсивности деформаций ε i, одна и та же, т.е.
σ i (ε i) = const. (9)
где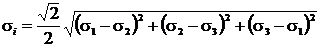 
, 
, если деформация рассматривается в главных осях.
Поскольку при растяжении σ2=σ3=0, то σ1=σ i, ε1=ε i,то зависимость σ i (ε i)получается непосредственно из опытов на растяжение. Кроме того, мы увидим в дальнейшем, что при помощи кривой σ(ε)можно получить численную характеристику структуры металла − статистическую энтропию. Как известно, именно структура определяет свойства металла, поэтому, описав ее при помощи интегрально-вероятностной функции − статистической энтропии, мы сможем разработать математический аппарат, позволяющий прогнозировать свойства металла в результате целого комплекса технологических операций.
Кривую σ(ε)можно использовать для моделирования любого из процессов пластической обработки металлов, если ее описать какой-либо математической формулой. Одним из критериев, влияющих на выбор физических гипотез и математических моделей, является простота, поэтому часто рекомендуют избирать простейшую гипотезу из всех совместимых с результатами эксперимента. Такой подход согласуется с правилом бритвы, сформулированным монахом Оккамом около семисот лет назад. Этого правила придерживаются многие исследователи, а звучит оно приблизительно так: «Нет нужды выискивать сложные трактовки какого-либо явления, если его можно объяснить более простыми причинами. Отсекай (бритвой) сложное, если можно обойтись простым». Иногда это правило называют критерием простоты.
За 250 лет исследования и аппроксимации кривых s(ε) предложено несколько десятков формул, в том числе двухпараметрические
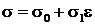, (10-1)
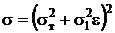, (10-2)
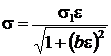, (10-3)
, (10-4)
, (10-5)
, (10-6)
. (10-7)
Наиболее популярны трехпараметрические формулы типа
, (11)
а также полиномы вида
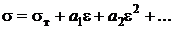, (12)
где параметры уравнений σ1, а i, α, β определяются экспериментально.
Цель работы: освоение методик испытаний металлов на растяжение и определения прочностных и пластических свойств деформируемого металла; освоение методики построения зависимости истинных напряжений от деформаций; освоение методики аппроксимации экспериментальной кривой σ(ε).
