Результаты расчета разностей по столбцам

ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Краткая теория, справочные таблицы и основные уравнения изложены в [1].

Задача 1: Провести дисперсионный анализ данных, представленных в таблице 1, при доверительной вероятности α=0,95.

Таблица 1

Результаты испытаний

Номер наблюдения j, (j =1… n)	Уровни фактора Аi (i =1… k)
	A1	A2	A3	A4	A5
1 2 3 4 5 6	3,2 3,1 3,1 2,8 3,3 3,0	2,6 3,1 2,7 2,9 2,7 2,8	2,9 2,6 3,0 3,0 3,0 2,8	3,6 3,4 3,2 3,3 3,5 3,3	3,0 3,4 3,0 3,5 2,9 3,1
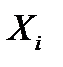
	18,5	16,8	17,4	20,3	19,1

 

Решение

Вычисляем суммы

 

Вычисляем дисперсии

 

Из таблиц для m ₁ = k -1 =4 и m ₂ = k (n -1) =25 находим F_0,95(4; 25)=2,8.

Так как >F_0,95(4;25)=2,8, влияние фактора А на отклик следует признать значимым.

Варианты заданий

Принятьрезультаты испытаний по примеру, заменив значения величин для одного уровня фактора согласно таблице 2.

Таблица 2 – Исходные данные

№ вар.	Результаты испытаний для уровня фактора А1
1	3,0	3,1	3,1	2,8	3,3	3,0
2	3,0	3,5	3,1	2,8	3,3	3,0
3	3,0	3,5	3,0	2,8	3,3	3,0
4	3,0	3,5	3,1	2,7	3,3	3,0
5	3,0	3,5	3,1	2,8	3,0	3,0
6	3,0	3,5	3,1	2,8	3,3	3,9
7	2,5	3,5	3,1	2,8	3,3	3,0
8	3,0	4,0	3,1	2,8	3,3	3,0
9	3,0	3,5	2,8	2,5	3,3	3,0
10	3,0	3,3	3,1	2,8	3,3	3,0
11	3,0	3,4	3,1	2,8	3,3	3,0
12	3,0	3,5	3,5	2,8	3,3	3,0
13	3,0	3,5	3,7	2,8	3,3	3,0
14	3,0	3,5	3,1	2,2	3,3	3,0
15	3,0	3,5	3,1	2,4	3,3	3,0
16	3,0	3,5	3,1	2,1	3,3	3,0
17	3,0	3,5	3,1	2,8	3,5	3,0
18	3,0	3,5	3,1	2,8	3,7	3,0
19	3,0	3,5	3,1	2,8	3,3	3,8
20	3,0	3,5	3,1	2,8	3,3	4,0
21	3,3	3,5	3,1	2,8	3,3	3,0
22	3,0	3,25	3,1	2,8	3,3	3,0
23	3,0	3,5	3,18	2,8	3,3	3,0
24	3,0	3,5	3,19	2,8	3,3	3,0
25	7,0	3,5	3,1	2,8	3,3	3,0

ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Краткая теория, справочные таблицы и основные уравнения изложены в [1].

Задача 2: Провести двухфакторный дисперсионный анализ данных, представленных в таблице 3, при доверительной вероятности α=0,95.

 

Таблица 3

Результаты исследования

В j (j=1…m	А i (i=1…k)
	А1 (ν=1…n)	А2 (ν=1…n)	А3 (ν=1…n)
В1 В2 В3 В4	3,6  3,8 4,1 4,2 4,0 4,1 3,8 3,5 3,6 3,4 3,2 3,2	2,9 3,1 3,0 3,3 2,9 3,2 3,6 3,7 3,5 3,4 3,6 3,5	2,6 2,5 2,9 3,7 3,5 3,6 3,2 3,0 3,4 3,6 3,8 3,7

 

Заменяя серии значений их средними, получаем следующую таблицу 4.

 

Таблица 4

Усредненные результаты исследования

В j (j=1…m)	А i (i=1…k)
	А1	А2	А3
В1 В2 В3 В4	3,83 4,10 3,63 3,27	3,00 3,13 3,60 3,50	2,67 3,60 3,20 3,70	9,50 10,83 10,43 10,47
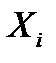
	14,83	13,23	13,17	41,23

Решение

 

- Используя данные таблицы, вычисляем суммы:

- Далее вычисляем дисперсии:

- Из таблиц (например, [8]) имеем F_0,95[ f ₁; f ₂ ]:

Для фактора А: F_0,95[ k -1;(k -1)*(m -1) ]= F_0,95(2; 6)=5,1;

Для фактора В: F_0,95[ m -1;(k -1)*(m -1)]= F_0,95(3; 6)=4,8.

Для фактора C=А*В: F_0,95 [(k -1)*(m -1); m * k *(n -1) ]= F_0,95(6; 24)=2,5.

 

- Сравнивая, получаем:

Следовательно, влияние факторов А и В должно быть признано незначимым.

 Однако существенно значимым является взаимодействие факторов А и В. Это поучительный пример эффективности двухфакторного дисперсионного анализа по сравнению с простым последовательным повторением однофакторных экспериментов.

Варианты заданий

Принятьрезультаты испытаний по примеру (таблицы 3), приняв значения строки В₁, для ν=3 из таблицы 5.

Таблица 5 – Исходные данные

№ вар.	Результаты испытаний для уровня фактора А1
1	3,83	3,1	2,67
2	3,6	3,1	2,67
3	3,83	3,1	2,5
4	3,7	3,1	2,67
5	3,83	3,0	2,67
6	3,83	3,1	2,5
7	3,68	3,1	2,67
8	3,83	3,2	2,67
9	3,83	3,1	2,57
10	3,44	3,1	2,67
11	3,83	2,85	2,67
12	3,83	3,1	3,1
13	3,3	3,1	2,67
14	3,2	3,1	2,67
15	3,1	3,1	2,67
16	3,0	3,1	2,67
17	3,83	2,9	2,67
18	3,83	2,8	2,67
19	3,83	2,7	2,67
20	3,83	2,6	2,67
21	3,83	2,5	2,67
22	3,83	3,1	2,9
23	3,83	3,1	3,1
24	3,83	3,1	3,2
25	3,83	3,1	3,3

ДИСПЕРСИОННЫЙ АНАЛИЗ С ИСПОЛЬЗОВАНИЕМ РАЗМАХОВ

Краткая теория, справочные таблицы и основные уравнения изложены в [1].

Задача 3: Провести дисперсионный анализ в условиях задачи 2 с помощью размахов. Исходные данные представлены в таблице 6.

 

Таблица 6

Исходные данные

В j (j=1…m)	А i (i=1…k)
	А1	А2	А3
В1 В2 В3 В4	3,83 4,10 3,63 3,27	3,00 3,13 3,60 3,50	2,67 3,60 3,20 3,70	9,50 10,83 10,43 10,47
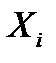
	14,83	13,23	13,17	41,23

Имеем k=3, m=4. Из таблицы 4.10 [1] для k=3, m=4 находим c=1,54 и f=5,4.

- Далее находим средние по столбцам (уровни фактора А):

Следовательно:

- Теперь для всех уровней фактора B при i -м уровне фактора А вычислим разности  для всех i=1,2,…,m.

Результаты сведены в таблицу 7.

Таблица 7

Результаты расчета разностей по столбцам

В j (j=1…m)	А i (i=1…k)
	А1	А2	А3
В1 В2 В3 В4	0,1225 0,3925 -0,0775 -0,4375	-0,3075 -0,1775 0,2925 0,1925	-0,623 0,307 -0,093 0,407	0,7455 0,5700 0,3700 0,8445

 

- Для каждого j значения приведены в последнем столбце таблицы 7.

- Далее находим:

Из таблицы для m=4 и f=5,4, при α=0,95 находим q_0,95(4; 5,4)=5,2.

Так как q=2,018 < q_0,95(4; 5,4)=5,2 - этот критерий не выявил влияние факторов А и В на наблюдаемый процесс. К сожалению, выделить влияние взаимодействия факторов А и В с помощью этого критерия невозможно.

 

Варианты заданий

Принятьрезультаты испытаний по примеру (таблицы 6), приняв значения строки В₁ из таблицы 9.

Таблица 9 – Исходные данные

 

№ вар.	Результаты испытаний для уровня фактора В 1
1	3,83	3,1	2,67
2	3,6	3,1	2,67
3	3,83	3,1	2,5
4	3,7	3,1	2,67
5	3,83	3,0	2,67
6	3,83	3,1	2,5
7	3,68	3,1	2,67
8	3,83	3,2	2,67
9	3,83	3,1	2,57
10	3,44	3,1	2,67
11	3,83	2,85	2,67
12	3,83	3,1	3,1
13	3,3	3,1	2,67
14	3,2	3,1	2,67
15	3,1	3,1	2,67
16	3,0	3,1	2,67
17	3,83	2,9	2,67
18	3,83	2,8	2,67
19	3,83	2,7	2,67
20	3,83	2,6	2,67
21	3,83	2,5	2,67
22	3,83	3,1	2,9
23	3,83	3,1	3,1
24	3,83	3,1	3,2
25	3,83	3,1	3,3