Пример 2.1. Отделить корни уравнения sin5 x + x 2 – 1 = 0.
Решение. Построим таблицу значений функции y = sin5 x + x 2 – 1 на отрезке [–4; 4] с шагом изменения аргумента h = 1, пользуясь калькулятором или электронными таблицами (табл. 2.1).
Табл. 2.1
| x | –4 | –3 | –2 | –1 | 0 | 1 | 2 | 3 | 4 |
| y | 14,087 | 7,349 | 3,544 | 0,958 | –1 | –0,958 | 2,455 | 8,650 | 15,912 |
Табл. 2.1 показывает, что данное уравнение имеет корни в интервалах
(–1; 0) и (1; 2), так как функция меняет знак в этих промежутках. Пока мы не можем утверждать, что в найденных интервалах содержится ровно по одному корню и, что в других интервалах корней нет. Чтобы уточнить информацию о числе корней можно построить таблицу значений функции с меньшим шагом, например h = 0,1.
Для отделения корней уравнения естественно применять графический метод. График функции y = f (x) с учетом свойств функции дает много информации для определения числа корней уравнения f (x) = 0.
Построим для примера 2.1 график функции в программе Excel на отрезке [–1, 2] с шагом изменения аргумента h = 0,1. Для этого выполним следующие действия в программе Excel:
1) В диапазоне A 2: A 32 введем значения переменной x. Для этого в ячейке A 2 запишем –1, в ячейке A 3 — значение –1,9. После этого выделим диапазон A 2: A 3 и с помощью маркера заполнения присвоим значения остальным ячейкам до ячейки A 32.
2) В ячейку B 2 введем формулу =SIN(5* A 2)+ A 2^2–1 и скопируем B 2 с помощью маркера заполнения в остальные ячейки до ячейки B 32.
3) Выделим диапазон A 2: B 32 и с помощью мастера диаграмм (тип диаграммы «Точечная, точечная диаграмма со значениями, соединенными отрезками без маркеров») построим график функции.
Полученный график представлен на рис. 2.1.
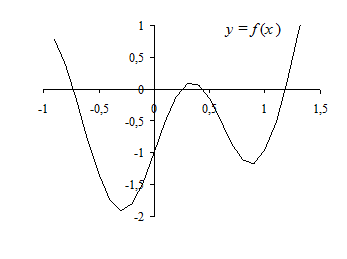
Рис. 2.1.
Из графика видно, что на отрезке [0; 0,5] есть два корня. Из таблицы A 2: B 32 значений функции заключаем, что уравнение имеет четыре корня в интервалах [–0,8; –0,7], [0,2; 0,3], [0,4; 0,5], [1,1; 1,2].
Чтобы убедиться в том, что больше корней нет, преобразуем уравнение к виду sin 5 x = 1 – x 2и построим графики двух функций f 1(x) = sin 5 x и
f 2(x) = 1 – x 2. Корням соответствуют абсциссы точек пересечения этих графиков. Так как значения первой функции ограничены и принадлежат отрезку [–1; 1], то подберем отрезок значений x для построения графиков так, чтобы за пределами этого отрезка значения второй функции были по абсолютной величине больше единицы. Искомые корни могут находиться только внутри этого отрезка. Очевидно, что отрезок [–2; 2] удовлетворяет этим условиям, так как при | x | > 2 выполнено неравенство | f 2(x)| > 1. Построим графики этих функций на отрезке [–2; 2] с шагом h = 0,2. Для этого в программе Excel выполним следующие действия:
1) В ячейке A 2 запишем –2, в ячейке A 3 значение –1,8. Выделим диапазон A 2: A 3 и с помощью маркера заполнения присвоим значения остальным ячейкам до появления значения 2 (до ячейки A 42).
2) В ячейку B 2 введем формулу =SIN(5* A 2) и скопируем B 2 с помощью маркера заполнения в остальные ячейки до ячейки B 42.В ячейку C 2 введем формулу =1– A 2^2 и скопируем C 2 с помощью маркера заполнения в остальные ячейки до ячейки C 42.
3) Выделим диапазон A 2: C 42 и с помощью мастера диаграмм (тип диаграммы «Точечная») построим графики функций.

Рис. 2.2
Из рис. 2.2 видно, что графики пересекаются в четырех точках и данное уравнение имеет ровно четыре корня, что подтверждает предыдущие выводы.
До настоящего времени графический метод предлагалось применять для нахождения грубого значения корня или нахождения интервала, содержащего корень, и затем применять итерационные методы, т.е. методы последовательных приближений для уточнения значения корня. С появлением математических пакетов и электронных таблиц стало возможным вычислять таблицы значений функции с любым шагом и строить графики с высокой точностью. Это позволяет уточнять очередной знак в приближенном значении корня при помощи следующего алгоритма:
1) Если функция f (x) на концах отрезка [ a, b ] принимает значения разных знаков, то делим отрезок на 10 равных частей и находим ту часть, которая содержит корень (таким способом мы можем уменьшить длину отрезка, содержащего корень, в 10 раз).
2) Повторим действия предыдущего пункта для полученного отрезка.
Этот процесс можно продолжать до тех пор, пока длина отрезка не станет меньше заданной погрешности.
Пример 2.2. Отделить корни уравнения sin x + x – 1 = 0.
Решение. Найдем производную функции f (x) = sin x + x – 1 и её корни:

Функция f (x) = sin x + x – 1 монотонна на отрезках [– π + 2π k, π + 2π k ]. Очевидно, что лишь отрезок [– π, π] содержит корень и он единственный.
Пример 2. 3. Вычислить графически с точностью до 0,0001 корень уравнения sin5 x + x 2 – 1 = 0, принадлежащий интервалу (0,4; 0,5).
Решение. Построим график функции y = sin5 x + x 2 – 1 на отрезке
[0,4; 0,5] с шагом h = 0,01 (делим отрезок на 10 частей) в программе Excel:
1) В диапазоне A 2: A 12 введем значения переменной x. Для этого в ячейке A 2 запишем 0,40, в ячейке A 3 — значение 0,41. После этого выделим диапазон A 2: A 3 и с помощью маркера заполнения присвоим значения остальным ячейкам до ячейки A 12.
2) В ячейку B 2 введем формулу =SIN(5* A 2)+ A 2^2–1 и скопируем B 2 с помощью маркера заполнения в остальные ячейки до ячейки B 12.
3) Выделим диапазон A 2: B 12 и с помощью мастера диаграмм (тип диаграммы “Точечная”!) построим график функции.
Лист Excel отображен на рис. 2.3.
|
| A | B | С | D | E | F | G | H | |
| 1 | x | y |
|
|
|
|
|
| |
| 2 | 0,4 | 0,069297 |
|
|
|
|
|
| |
| 3 | 0,41 | 0,055462 |
|
|
|
|
|
| |
| 4 | 0,42 | 0,039609 |
|
|
|
|
|
| |
| 5 | 0,43 | 0,021799 |
|
|
|
|
|
| |
| 6 | 0,44 | 0,002096 |
|
|
|
|
|
| |
| 7 | 0,45 | –0,01943 |
|
|
|
|
|
| |
| 8 | 0,46 | –0,04269 |
|
|
|
|
|
| |
| 9 | 0,47 | –0,06763 |
|
|
|
|
|
| |
| 10 | 0,48 | –0,09414 |
|
|
|
|
|
| |
| 11 | 0,49 | –0,12214 |
|
|
|
|
|
| |
| 12 | 0,5 | –0,15153 |
|
|
|
|
|
| |
| 13 |
|
|
|
|
|
|
|
| |
| 14 |
|
|
|
|
|
|
|
|
Рис. 2.3
Рис. 2.3 показывает, что корень находится в интервале (0,44; 0,45), так как функция меняет знак в точках 0,44 и 0,45.
Заменим значения переменной x на том же листе в диапазоне A 2: A 12, то есть вместо интервала (0,4; 0,5) подставим интервал (0,44; 0,45) с шагом h = 0,001. Для этого в ячейке A 2 запишем 0,440, а в ячейке A 3 — значение 0,441. Затем выделим диапазон A 2: A 3 и с помощью маркера заполнения присвоим значения остальным ячейкам до ячейки A 12. Формулы в ячейках B 2: B 12 не трогаем! В результате этого получим новую таблицу значений функции, из которой получаем уточненный интервал (0,441; 0,442).
Повторив всю процедуру еще раз, заменим в диапазоне A 2: A 12 интервал (0,44; 0,45) на интервал (0,441; 0,442) с шагом h = 0,0001. Искомый корень содержится в интервале (0,4410; 0,4411). Длина этого интервала равна 0,0001 и любое число из этого интервала можно принять за приближенное значение корня с погрешностью 0,0001. Выберем середину отрезка, т.е. положим x ≈ 0,44105.
В таблице 2.2 приведены все три этапа уточнения корня. Здесь мы не приводим соответствующие графики, так как для отделения корня достаточно рассмотреть таблицу значений функции и найти последовательные значения переменной x, в которых функция изменяет знак.
Аналогично можно уточнить значения других корней данного уравнения. Для этого достаточно на том же расчетном листе вместо отрезка
[0,4; 0,5] рассмотреть любой из оставшихся трех отрезков [– 0,8; – 0,7],
[0,2; 0,3], [1,1; 1,2].
Табл. 2.2
| 1–й этап. Интервал (0,4; 0,5) |
| 2-й этап. |
| 3-й этап. Интервал (0,441; 0,442) | ||||||
|
| A | B |
|
| A | B |
|
| A | B |
| 1 | x | y |
| 1 | x | y |
| 1 | x | y |
| 2 | 0,4 | 0,069297 |
| 2 | 0,44 | 0,002096 |
| 2 | ||
0,441







