Специальность 230701, 080214, 230113
Семестр 2
Формы контроля: решение заданий, собеседование
Последовательность и условия выполнения задания
1.Решение двух практических заданий (по билету).
2.Собеседование по 2-3 теоретическим вопросам, выбранным случайным образом из предлагаемого перечня.
Вы можете воспользоваться: -справочником формул, микрокалькулятором,
при сдаче на «удовлетворительно»: конспектом.
Максимальное время выполнения заданий – 40 мин.
Собеседование до 10 мин.
Теоретические вопросы
| 1. | Тригонометрические уравнения. Понятие arcsin a, arccos a, arctg a, arcctg a. Общие формулы для решения уравнений cos x=a, sin x=a, tg x=a, ctg x=a. |
| 2. | Исследование функций и построение графиков Алгоритм исследования функций (дополненный стационарными точками, промежутками монотонности, найденными по средствам производной). |
| 3. | Алгоритм нахождения точек экстремума функций, точек перегиба и разрыва. |
| 4. | Построение графиков функций y=xp, y=ax, y=logax, y=sin x, y=cos x, y=tg x, y=ctg x. |
| 5. | Решение уравнение уравнений графически. Алгоритм решения уравнений графически. Преимущества данного способа решений уравнений перед аналитическим. |
| 6. | Комбинаторика. Перестановки (понятие, определение, правило нахождения, типы задач, решаемые с помощью перестановок). |
| 7. | Размещения (понятие, определение, правило нахождения, типы задач, решаемые с помощью размещений). |
| 8. | Сочетания (понятие, определение, правило нахождения, типы задач, решаемые с помощью сочетаний). |
| 9. | Свойства сочетаний. Бином Ньютона. Треугольник Паскаля. |
| 10. | Теория вероятностей. Определения события, элементарного события, достоверного события, невозможного события, несовместного события, равновозможного события, единственно возможного события, противоположного события. |
| 11. | Равносильные события. Сумма и произведение событий. |
| 12. | Определение вероятности события, формула для нахождения вероятности. |
| 13. | Сложение вероятностей несовместных событий. Сумма противоположных событий. |
| 14. | Независимые события. Умножение вероятностей независимых событий. |
| 15. | Статистическая вероятность. Частота события. Относительная частота. |
| 16. | Случайные величины, полигон частот, гистограмма частот. |
| 17. | Центральные тенденции: мода, медиана, среднее арифметическое, математическое ожидание. |
| 18. | Генеральная совокупность, репрезентативная выборка. |
| 19. | Меры разброса: размах, стабильность, отклонение от среднего, дисперсия, среднее квадратичное отклонение от среднего. |
| 20. | Решение неравенств. Алгоритм решения иррациональных неравенств. |
| 21. | Алгоритм решения показательных неравенств. |
| 22. | Алгоритм решения логарифмических неравенств. |
| 23. | Тригонометрические неравенства – графический способ решения с использованием единичной окружности. |
| 24. | Алгоритм решения систем уравнений. |
| 25. | Числовая последовательность: понятие, определение. Ограниченность, монотонность. |
| 26. | Предел числовой последовательности: понятие, определение. |
| 27. | Свойства и правила нахождения пределов, оценка результата по виду последовательности. |
| 28. | Раскрытие стандартных неопределенностей дроби, правила нахождения. |
| 29. | Производная функции. Определение производной функции через предел разностного отношения. |
| 30. | Правила дифференцирования. |
| 31. | Таблица производных некоторых элементарных функций. |
| 32. | Физический и геометрический смысл производной. |
| 33. | Стационарные точки, точки максимума и минимума, точки разрыва, перегиба, точки экстремума функции. |
| 34. | Применение производной к построению графиков функций. |
| 35. | Нахождение наибольшего и наименьшего значения функции на отрезке. |
| 36. | Определение первообразной функции, понятие. Таблица первообразных функций. |
| 37. | Неопределенный интеграл. Правила интегрирования. |
| 38. | Определенный интеграл. Нахождение определенных интегралов. Формула Ньютона-Лейбница. |
| 39. | Криволинейная трапеция. Нахождение площади криволинейной трапеции. |
| 40. | Фигуры пространства: общий вид, понятие, чертеж, способы построения, элементы. |
| 41. | Формулы объема, площади боковой и полной поверхности призмы, прямоугольного параллелепипеда, куба. |
| 42. | Формулы объема, площади боковой и полной поверхности пирамиды (в том числе правильной и усеченной). |
| 43. | Формулы объема, площади боковой и полной поверхности цилиндра, конуса (в том числе усеченного). |
Типовые практические задания
1. Вычислить

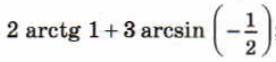



2. Решить уравнение
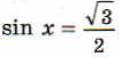
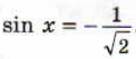




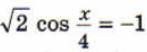

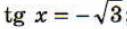

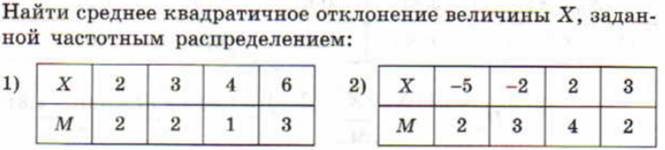
3. Решить задачу

















4. Решить уравнение


5. Записать разложение бинома
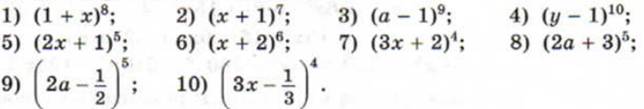
6. Заполнить таблицу с точностью до сотых

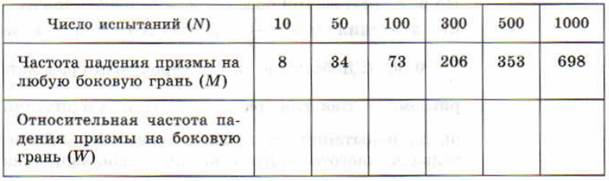
7. Решить систему уравнений





8. Решить неравенства
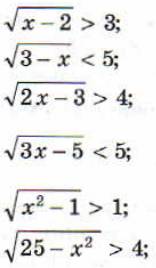







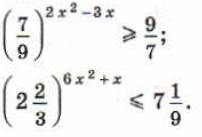





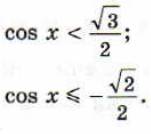

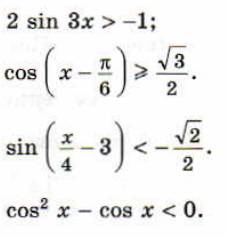
9. Найти производную функции с помощью правил дифференцирования и таблицы производных элементарных функций


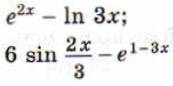




10. Используя геометрический смысл производный решить задачи

11. Найти стационарные точки функции и указать их вид, определить промежутки монотонности функции

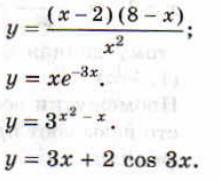
12. Найти точки экстремума функции, построить эскиз графика

13. Найти наибольшее и наименьшее значение функции на отрезке

14. Найти одну из первообразных для функций

15. Найти все первообразные для функций

16. Используя формулу Ньютона-Лейбница решить задания

17. Вычислить интеграл
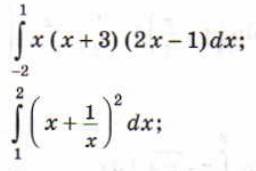




18. Задачи на нахождение объемов тел и площадей их поверхностей 












Методика и критерии оценки
Оценка






